语法分析关键知识点小结
LL
自顶向下解析 可以细分为 两种: 递归下降解析 和( ) ,其中递归下降解析又有两种实现方式,回溯法和 预测解析 ,其中预测解析通过预读字符来实现,其预读的个数也作为一个环境变量。
预读k个字符的预测解析 法 被称为:
LL(k)文法, 其中第一个L表示从左向右扫描输入字符串 ;第二个L表示LeftMost(最左推导)
k表示预读 k个字符。
如何判断文法是不是有二义性
==尝试的时候就看,没有确定优先级和结合性一般就会导致二义性了==
定义 10 用二义性甩. 如果对于一个文法,存在一个句子,对这个句子可以构造两棵不同的分析树,那么我们称这个文法为二义的
所以找到两个不同分析树即可,例如:

优先级和结合性:
若文法G对同一句子产生不止一棵分析树,则称G是二义的。
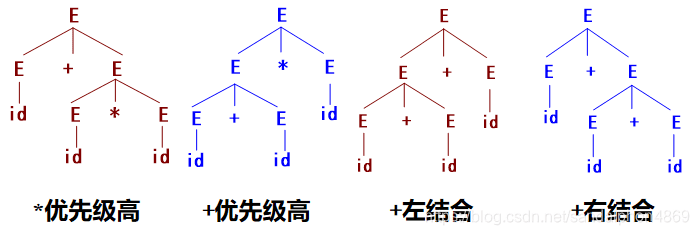
例3.7 句子id+id*id和id+id+id可能的分析树
E→E+E | E*E |(E)| -E | id
深度越深,越远离开始节点,优先级越高。
非终结符在终结符(如+)的左边是左结合,右边是右结合。

如何判断是不是LL文法
Top-down + predict = LL(K)
如果有以下两项则不是LL(K)文法(lec_7,P35)
- 有共同前缀
- 有左递归
幸运的是有办法可以消除这两个。
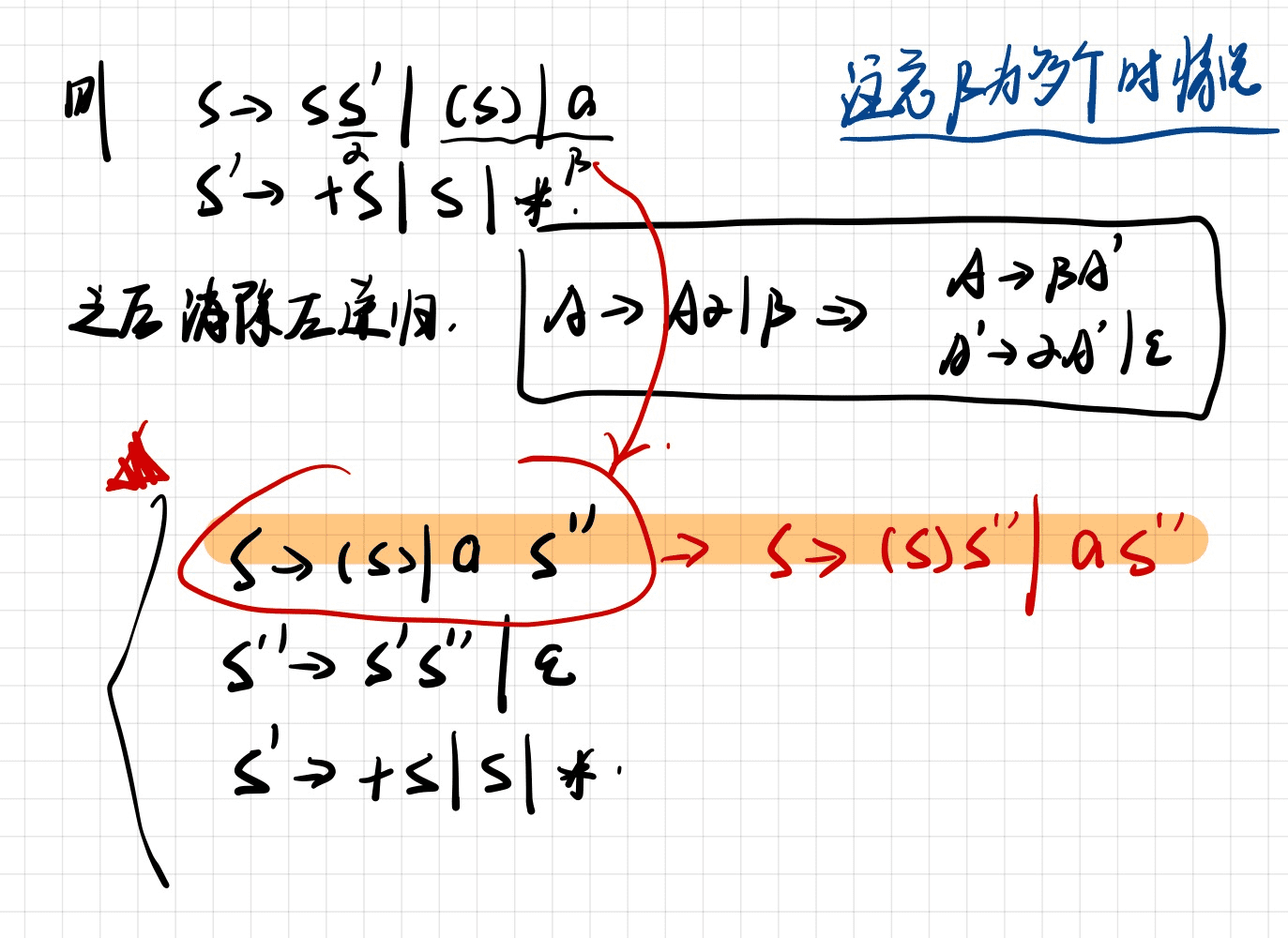
如何变为LL文法
==建议先消除共同前缀,然后再消除左递归,例如hw2的1.5==
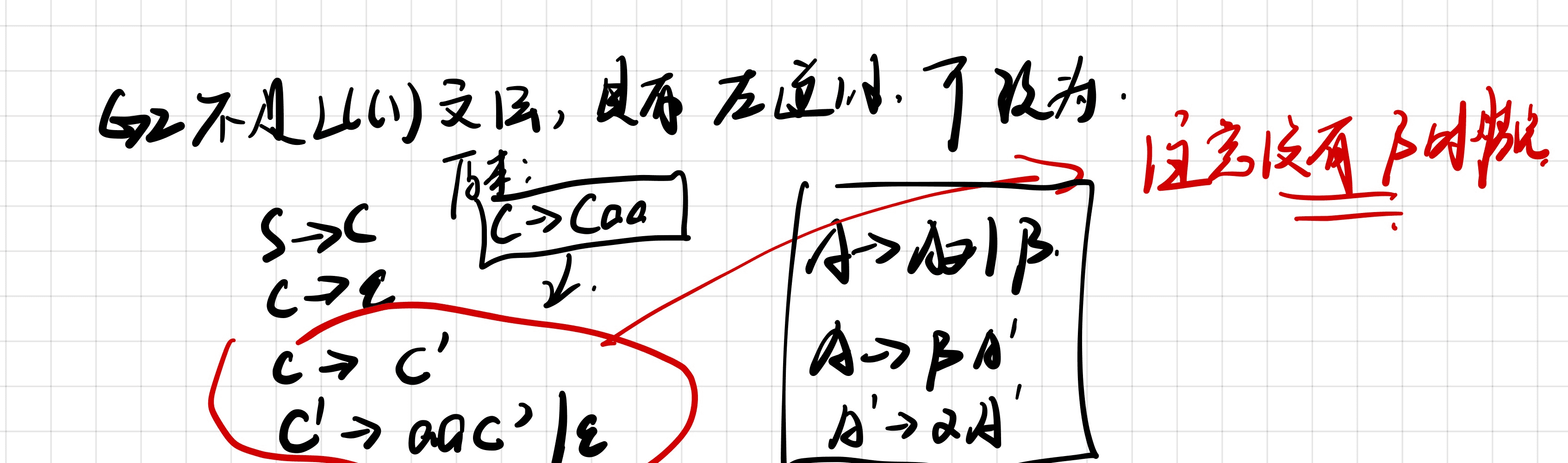
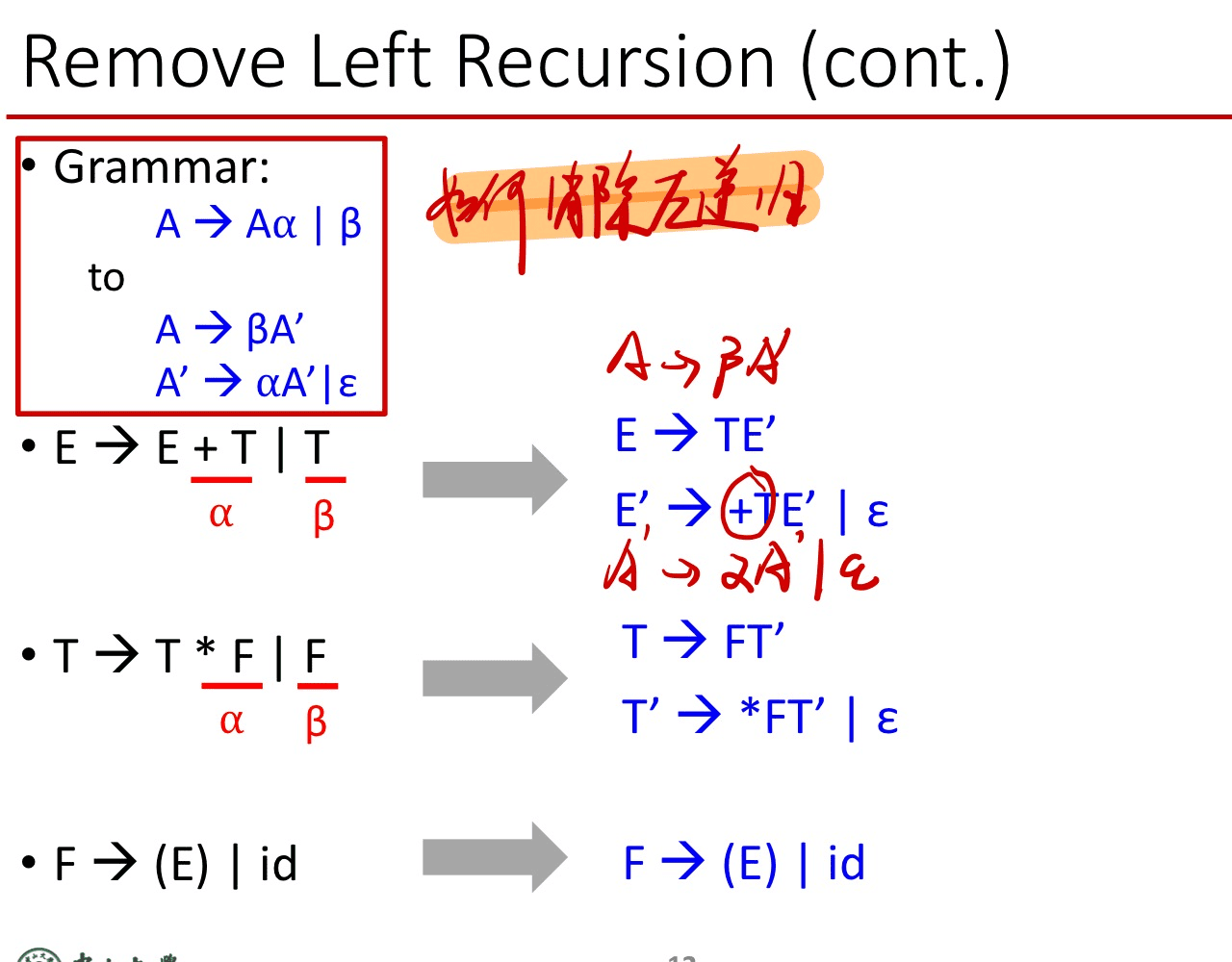
如何消除左递归
更一般情况下的直接左递归
考虑如下文法:
| A→Aα1 | Aα2 | … | Aαm | β1 | β2 | … | βn |
产生的句子为:
βiαj1αj2…
所以,消除递归后文法为:
A→(β1|β2|…|βn)A’ 用来产生以βi开头的句型/句子
A’→(α1|α2|…|αm)A’|ε
\(\begin{align*}
A &\rightarrow A\alpha \\
&\rightarrow A\alpha \alpha \\
&\rightarrow A\alpha \alpha \alpha
\end{align*}\)

易错点例子
==β为多个时==
==没有β时==
如何消除共同前缀

First集、Follow集和Select集
定义 15
-
FIRST(α)为从α中推导出来的字符串第一个终端符号的集合
-
FOLLOW(A)集为可以出现在A右侧的终端符号的集合
FOLLOW(A)是所有该文法开始符推导的句型中出现在紧跟A之后的终结符或 “#”。 \(follow(A)=\{a|S\to...Aa...,a\in V_t\}\) 其中S表示文法的开始符号,非终结符A后面跟着的终结符或‘#’集合,且是紧挨着A的
如何求First集
求$First(X)$
-
如果$X$是终结符,则$First(X)={X}$
-
如果$X$是非终结符且存在$X\to \varepsilon $,则将$\varepsilon$加入到$First(X)$中
-
若$X→Y…$,且$Y$属于非终结符且$Y$不能推出$\varepsilon$,则将$FIRST(Y)/{\varepsilon}$加入到$FIRST(X)$中。
也就是第一个非终结符的$First$集就不包含$\varepsilon$(换句话说第一个非终结符不能推出$\varepsilon$)
-
如果$X$是非终结符且$X \to Y_1Y_2Y_3…Y_k$,则
-
若$Y_1Y_2Y_3…Y_k$都是非终结符,且$Y_1Y_2Y_3…Y_{i-1}$的$FIRST$集合中均包含$\varepsilon$,则将$FIRST(Y_j),(j=1,2…i)$的所有非$\varepsilon$元素加入到$FIRST(X)$中,
==也就是找到第一个$First$集里不包含$\varepsilon$的的$Y_i$==,然后将$Y_0到Y_i$的$First$集合都加入到$First(X)$中。
这里很容易忘记是要找到第一个不包含$\varepsilon$的symbol
例如:如果X是非终结符,有产生式形如$X\to ABCdEF…$(A,B,C为非终结符且包含ε,d为终结符,也就是说First(d)={d}不包含$\varepsilon$),则需要把FIRST(A), FIRST(B),FIRST(C),First(d)={d}入到FIRST(X)中
-
==特别地,若$Y_1Y_2Y_3…Y_k$均有$\varepsilon$产生式,则将$\varepsilon$加到$FIRST(X)$中。==
-
所以可以总结为直到找到后面不能推出空的,然后累加前面的所有的First集
技巧:
==First一般从下往上找。==
如果要找A的First,我们要找A的定义式,即A在左边的式子,看着他的右边来找。
如何求Follow集
如何求$Follow集$(==非终结符才有==),所以求follow集的时候先找非终结符
-
如果是文法的开始符号S,把$$$加入到$Follow(S)$
-
如果有$A\toαBβ$,则把$First(β)/{ε}$加入到$Follow(B)$中.(first(β)/{ε}表示把first(β)中去掉ε)
也就是这里B后面第一个不为空,所以可以直接将后一个的First集加入到$Follow(B)$中
-
如果有$A\to αB$或$A\to αBβ$,且$β\toε$(这个条件应该是First(β)包含ε),则把$Follow(A)$加入到$Follow(B)$中。
注意,A->αBβ,α可以是终结符也可以为非终结符也可以为空,没影响,因为Follow看的是B后面可以是什么符号,β可以为终结符或者非终结符,但是不能为空且B后面要有符号;
==注意这里要按顺序走完,满足2的同样有机会满足3,(有$β\toε$)==
| 如S->(L) | aL | LC |
找Follow的三种情况:
先在候选式(右边)中找到该非终结符,如L(注意例中只有一个定义,但找Follow要看到所有右边出现该非终结符的)
- 如果L的右边是终结符, 那么这个终结符加入L的$Follow$(其实这一个是第二个情况的一部分,因为如果L右边是终结符,也就是$β$是终结符,那么$First(β)={β}$,所以相当于是把这个终结符加入$Follow集$)
- 如果L的右边是非终结符, 那么把这个非终结符的$First$除去空加到L的Follow中
- 如果L处在最末尾(右边没有东西了),那么,$\to$左手边符号的$Follow$集加入到L的$Follow$集。
小结: FOLLOW集对于非终结符而言,是非终结符的全部后跟符号的集合,
如果后跟终结符则加入,
如果后跟非终结符,则加入该非终结符的不含空符号串的FIRST集,
特别地,文法的开始符号的FOLLOW集需要额外的加入‘#’。
1
技巧
==Follow一般从上往下找。==
如果要找L的Follow,要从式子的右边找到非终结符L,然后来找L的Follow,这与First是不同的。
如何求Select集
定义:给定上下文无关文法的产生式$A→α, A∈VN,α∈V*$
如何求:(α是一个整体,例如 ,其中第一个A可以推出空,所以还需要求B的first,所以First(AB)={a,b})
,其中第一个A可以推出空,所以还需要求B的first,所以First(AB)={a,b})
- 若α不能推导出ε则:SELECT(A→α)=FIRST(α)
- 如果α能推导出ε则:SELECT(A→α)=(FIRST(α) –{ε})∪FOLLOW(A)
也可以
先只考虑first集
然后考虑如果 ε 在 FIRST(α) 中,或者 α=ε,则 a 在 FOLLOW(A) 中(ε-产生式)
如果 ε 在 FIRST(α) 中并且 $ 在 FOLLOW(A) 中,则将 A 与 α 一起添加到 M[A, $]
例如:
易错点的例题( 来自HW2-3(1) ):
需要注意的是,SELECT集是针对产生式而言的。
意义:给定输入的表达式字符串,需要根据表达式的字符串中的字符用来寻找正确的产生式,即输入的表达式字串中的字符作为key,产生式作为value,那么这个select集就是构造的map
例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
G(E):
E->TE'
E'->+TE' | ε
T->FT'
T'->*FT' | ε
F->(E) | i
对应的first集合:
first(E) = {i, (}
first(T) = {i, (}
first(E') = {+, ε}
first(T') = {*, ε}
first(F) = {(, i}
对应的follow 集合:
follow(E) = {#, )} // E作为开始符,且在F->(E) | i 产生式中,E后存在 ) 符号
follow(E') = {#, )} // 根据规则 A->αB,则E->TE'将follow(E)加入到follow(E')
follow(T) = {+, #, )} // 有E->TE',根据A->αBβ规则,有α为空,E'->ε,此时将follow(E)加入follow(T),根据E'->+TE' | ε将first(+)\{ε}加入follow(T)
follow(T') = {+, #, )} // T->FT'将follow(T)加入
follow(F) = {(*,+,#,)} // T->FT',根据A->αBβ,α为空,T'->ε,将follow(T)加入;T'->*FT' | ε,根据A->αBβ,将first(T') / {ε} 加入
那么计算的Select集是
1
2
3
4
5
6
7
8
select(E->TE') = {i, (} // T无法推出ε,所以取first(T)
select(E'->+TE') = {+} // 直接取first(+)
select(E'->ε) = {#, )} // 注意候选式要分开计算,因为是ε所以取follow(E')
select(T) = {(,i} // first(F)
select(T'->*FT') = {*} // first(*)
select(T'->ε) = {+, #, )} // follow(T')
select(F->(E)) = {(} // first(()
select(F->i) = {i} // first(i)
参考:First集 Follow集 Select集 知识点+例题
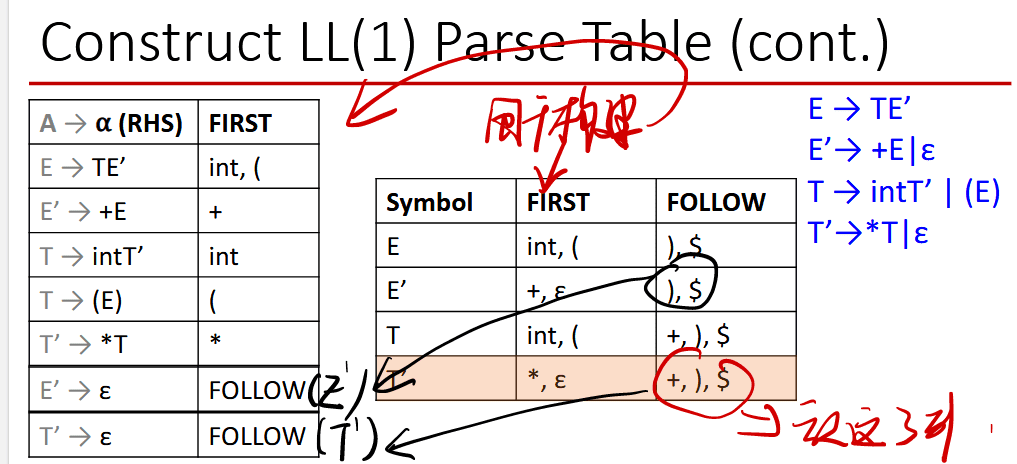
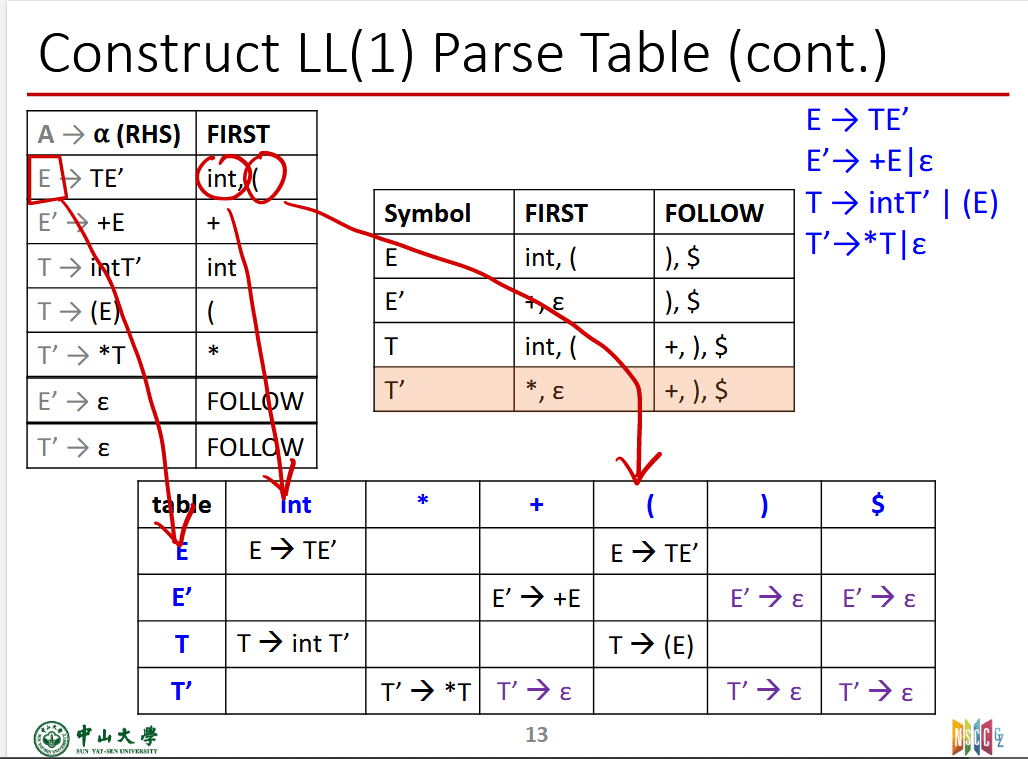
利用select集构建Parse Table
根据select表决定放在哪一列
如何判断是否符合LL(1)文法
确定文法是否为 LL(1) 的两种方法:
-
构造LL(1)表,检查如果每个格子中只有一条产生式,那么则是LL(1)
-
观察所有Select集,若左部相同的产生式的Select集的交集为空,则符合LL(1)文法,否则不满足。
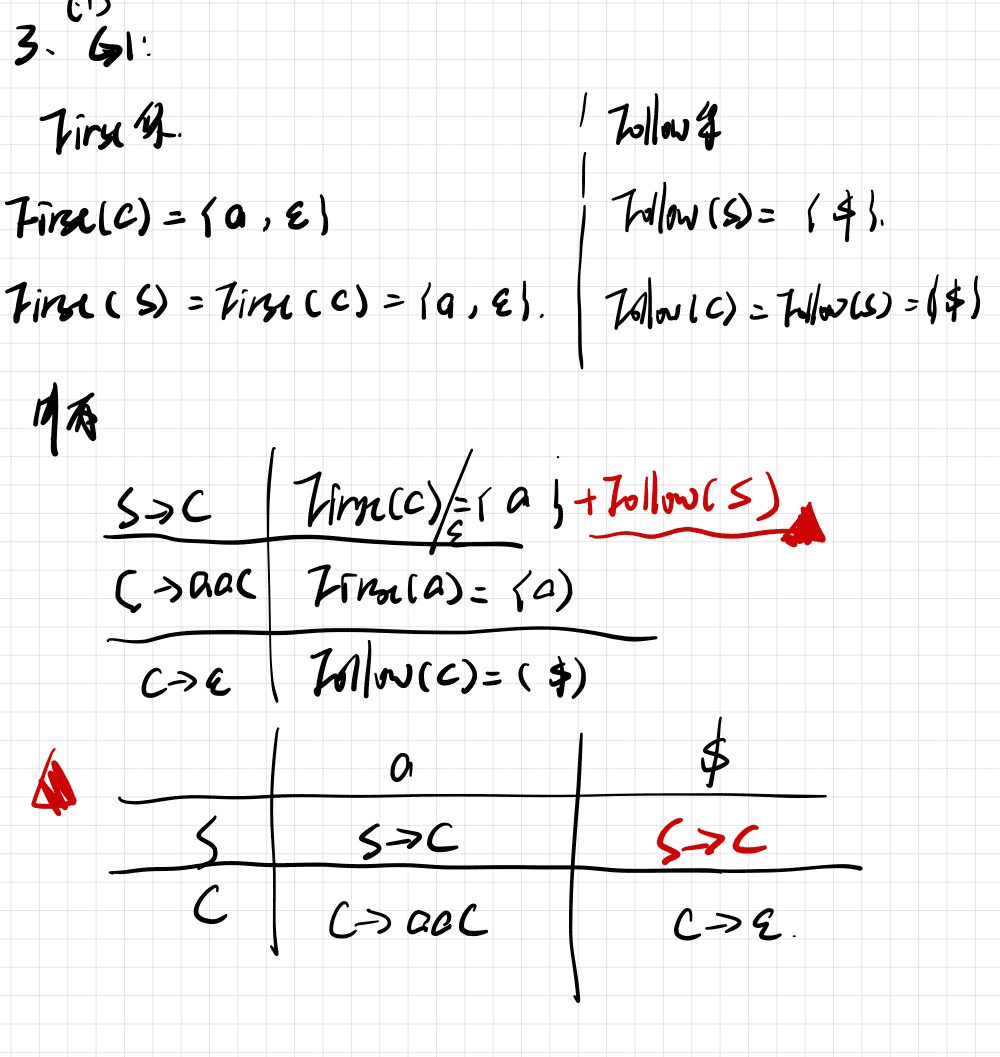
如何构造LL(1)的预测语法表
- 变为适合LL文法
- 计算First集和Follow集
- 根据First集和Follow集计算Select表
- 根据Select表画出预测语法表
用Select表将每个产生式放到产生式左部非终结符所对应的行,列表中各个终结符所对应的列
例如:
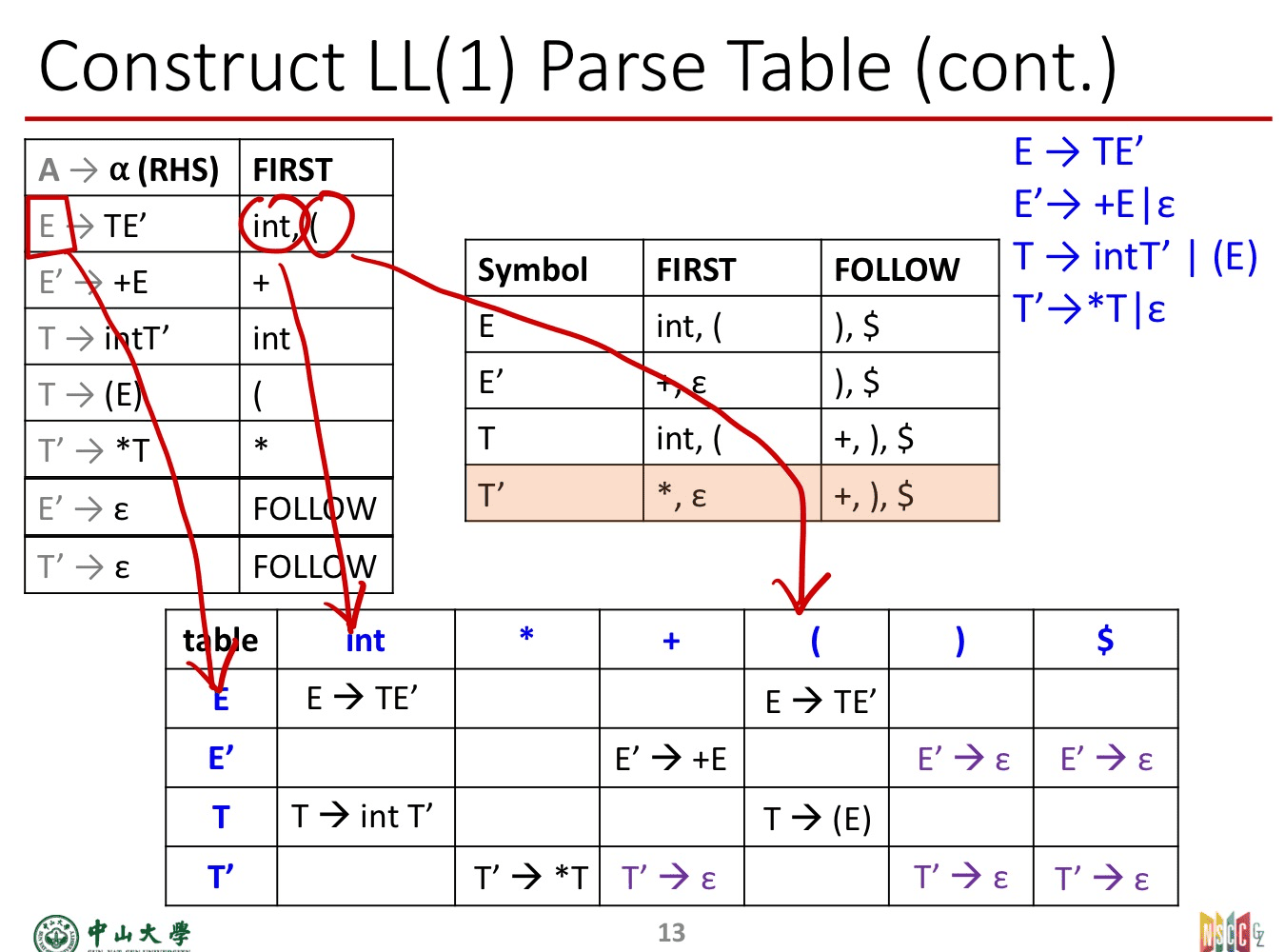
如何使用LL(1)的预测语法表、
X为栈顶symbol,a为目前input buffer中处理的token
-
比较(Match):栈顶X为终结符出栈查表对比
- $X==a==$$,那么返回success
- $X==a!=$$,那么属于中间过程,将X和a弹出即可
- $X!=a$$,paser halt and input is rejected
-
展开(Expand):栈顶X为非终结符出栈展开
-
如果MA[X,a] == ‘X->RHS’,那么X出栈,RHS入栈,input buffer中不变
入栈的时候是逆序入栈,例如X->BcD 其实也就是最左推导,最左边符号需要先被展开/比较,所以需要在靠近栈顶的位置。
之前的栈 之后的栈 B c X D … … $ $ -
如果MA[X,a] == empty,paser halt and input is rejected
-
LR
LR 文法,自底向上的语法分析
首先介绍 规约 的概念 ,自底向上的分析 和 自顶向下是反过来的,每次操作都是将 语法符号序列 转为非终结符 。(这与 自顶向下非终结符展开为语法符号序列恰好相反)
也就是从右往左替换,例如A->B,LL中是A被B替换,而LR中是用A替换B
自底向上 对应 反向最右推导(自顶向下 对应 最左推导)
例如:下面举个例子: \(id*id=>dF*id=>T*id=>T*T=>T=>E\) 如果反过来: \(E=>T=>T*F=>T*id=>F*id=>id*id\) 发现正好是一个最右推导
例子(lec-10):
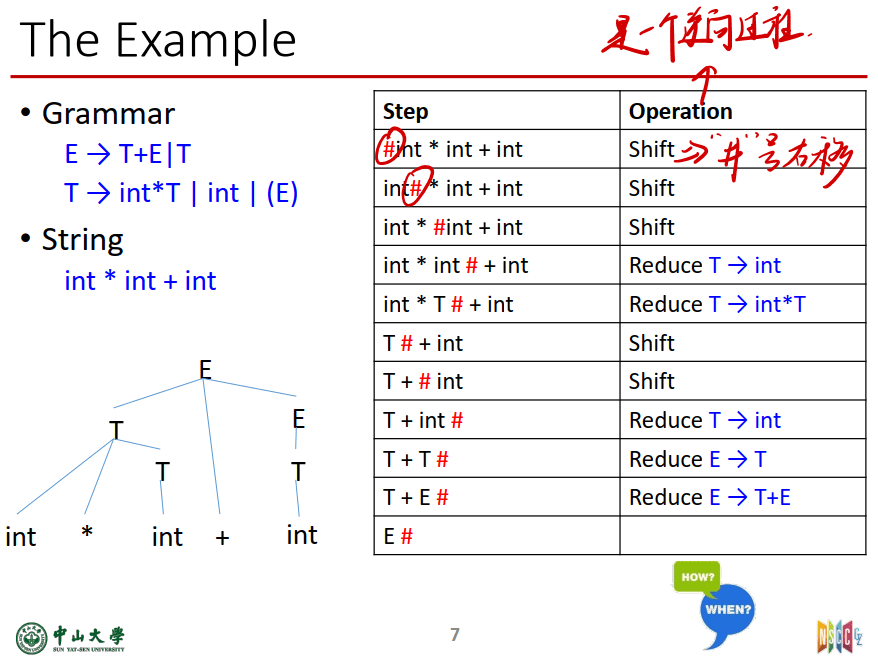
先科普下LR语法分析器的优势:
- 更通用:对于几乎所有程序设计语言,只要能写出上下文无关文法,就能够造出识别该语言的LR语法分析器。确实存在非LR的上下文无关文法,但常见程序设计语言都可以避免这种文法。
- 已知的最通用的 无回溯 移入-规约分析技术,其实现十分高效。
- 能尽早的发现语法错误,可以解决左递归问题
- LR的语言是LL语言的 真超集(也就是$LL \subseteq LR$)。LR文法的要求比LL文法要求宽松,且与LL一样高效
缺点:手工构造LR分析器的工作量非常大,但是可以利用LR语法分析器生成工具。比如Yacc等。
分界点用 # 标记(#号左边即为已经处理过的,右边为还没处理的)
- # 仅作为标示,不是字符串的一部分
- 最初,所有输入都是未经检查的,例如: $ # x1 x2 . . .xn$[输入尚未有任何解析]
自下而上的解析也称为 Shift-Reduce 解析
-
涉及两种类型的操作:Shift和Reduce
回顾:LL(自顶向下)中也是只有两种动作:expend和compare
-
Shift[移入]:向右移动 # 一个位置[向左侧移入终结符,推进解析]
-
ABC#xyz ⇒ ABCx#yz
-
Reduce[归约]:逆向使用产生式[左侧串的右端进行归约](#号左边的句柄规约)
- 如果 E → Cx 是产生式,那么:ABCx#yz ⇒ ABE#yz
我们用栈来实现,
#号左边字符串存储到堆栈中,堆栈的顶部是 #[#号左右串的分界]
-
Shift就是将终结符放到栈中
-
Reduce 执行以下操作(例如右产生式LHS -> RHS):
- 从堆栈中弹出零个或多个符号[pop出了产生式RHS]
- 在堆栈上推进非终结符[push进了产生式LHS]
其实就是反向使用产生式LHS <- RHS
下面介绍 移入-规约 语法分析技术 ,实际上这是自底向上分析的基本算法框架,
其包含两个组件:1个栈 , 1个输入缓冲区 ;
主要由4 个操作组成:
1)移入:将下一个输入 符号 移入 栈顶
2)规约 :规约是对栈中的语法符号串进行规约,被规约的串右侧位于栈顶,语法分析器确定串左端
3)接收 :宣布语法分析过程成功完成
4)报错 :发现语法错误,执行错误恢复程序。
移入-规约 技术的关键在于 决定 何时进行 规约, 何时进行移入操作,这将在后文的具体实现中介绍方法。
句柄
一个关键的问题是何时进行Shift何时进行Reduce?
只有栈顶是句柄的时候才Reduce,其他时候都是Shift
实际上句柄就是产生式的替换 ,
如果有$ S=>^{rm*}\alpha A\omega =>^{rm}\alpha \beta \omega$
则我们称$ A->\beta $是 $\alpha\beta\omega $的一个句柄,为了简化起见,有时直接把 $\beta $称为句柄,其中 $\omega $只包含终结符号(最右推导,所以右边这里其实是已经处理完的,也即最右推导中已被完全展开 ,左边的尚未被完全展开 )。
回顾: $\omega $只包含终结符号,也就是句子,句型既包含终结符也包含非终结符
所以自顶向上分析的技术可以看成不断的替换句柄为非终结符 的过程。
如何找到句柄?
- 最右句型:最右句型是指在语法分析过程中,通过逐步应用产生式规则,从初始符号开始逐步推导出的一系列符号串中的最后一个。在自底向上的语法分析(如移进-归约分析)中,最右句型是分析栈顶部的符号串
- 短语:一个句型的语法树中任一子树的叶结点所组成的符号串都是该句型的短语
- 直接短语:只用一步就可以推导出
句柄是最左直接短语:
例子1:

例子2:

==句柄一定只出现在栈顶==
一些概念
例子:
活前缀/可动前缀
定义:一个可行前缀是一个最右句型的前缀,并且它没有越过该最右句型的最右句柄的右端
举例:S => bBa => bbAa,这里句柄是 bA,因此可行前缀包括 bA 的所有前缀:b, bb,
bbA),但不能是 bbAa(因为越过了句柄)
二义文法
有多个可能的动作,会导致冲突
例如:既可以像左边一样规约,也可以向右边一样移进
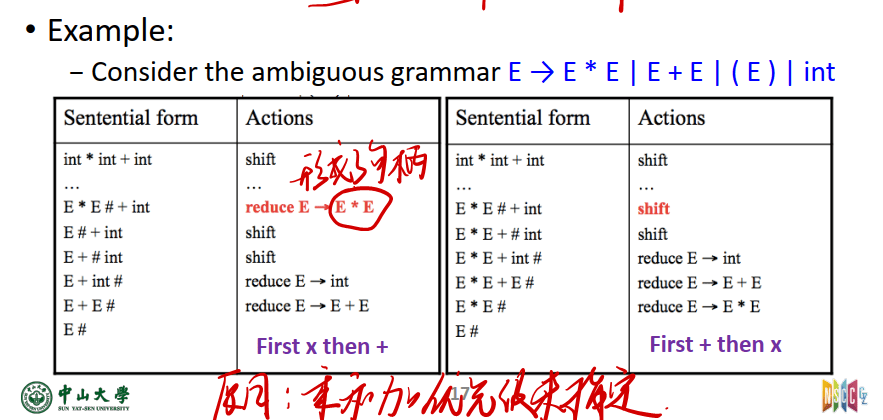
Can have conflicts[冲突可能发生]
- 如果Shift或Reduce是合法的,则存在Shift-Reduce conflict[移入-归约冲突]
- 如果有两个合法的Reduce,则有一个Reduce-Reduce conflict[归约-归约冲突]
- 没有Shift-Shift冲突这种东西
自底向上有很多种实现方式,但是我们只学LR类解析器,例如:LR(0), LR(1), SLR, LALR
LR(k):LR 解析器系列的成员
- L:从左到右扫描输入
- R:反向构造最右边的推导
- k:向前看k个
- k = 0 或 1 特别有意义,默认为 1
LR比LL更加powerful且一样高效
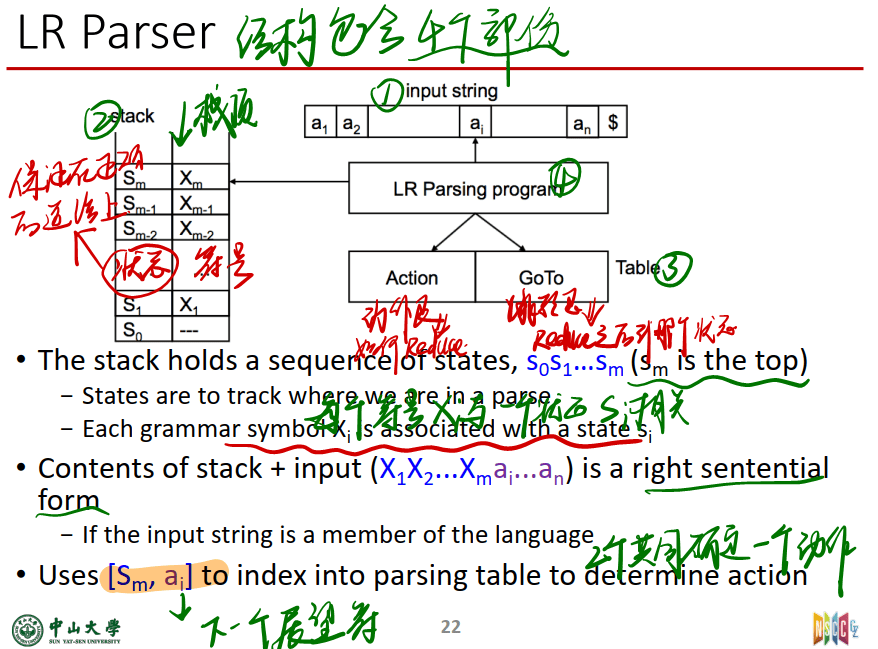
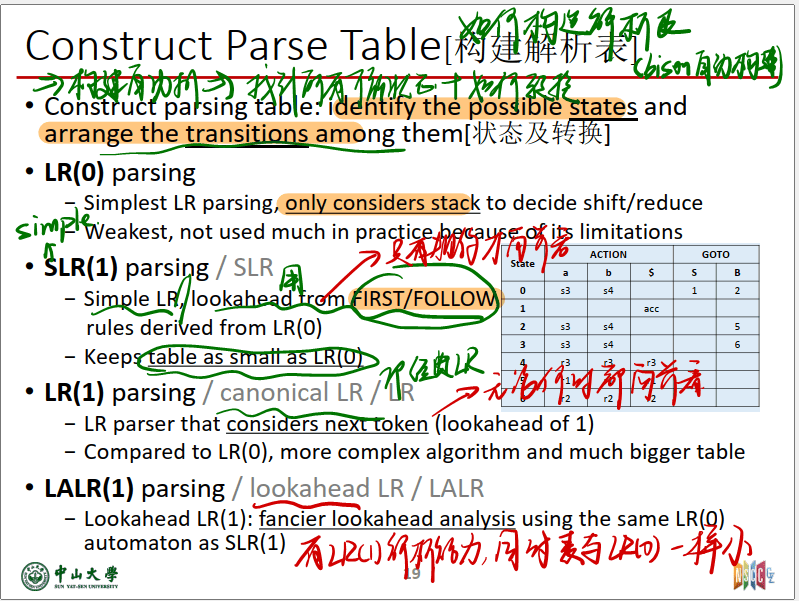
LR 解析器使用两个表:action表和goto表,这两个表通常合并在一起
-
action表指定终结符的条目(遇到终结符看action表)
-
goto表指定非终结符的条目(遇到非终结符看goto表)
其实是reduce之后看goto表,reduce得出的结果是非终结符,所以也可以说遇到非终结符看goto表
Action table[动作表](也就是用s+a确定下一个动作,a是终结符)
- Action[s, a] 告诉解析器当堆栈是 S,终结符 A 是下一个输入token
- 可能的操作:shift、reduce、accept、error
Goto Table[跳转表](也就是查看action表后发现是Reduce操作,Reduce发生后用S+x确定下一个状态,x是非终结符)
- Goto[s, X] 表示要放置在堆栈顶部的新状态,在非终结符X 的Reduce之后,状态 s 位于 堆栈
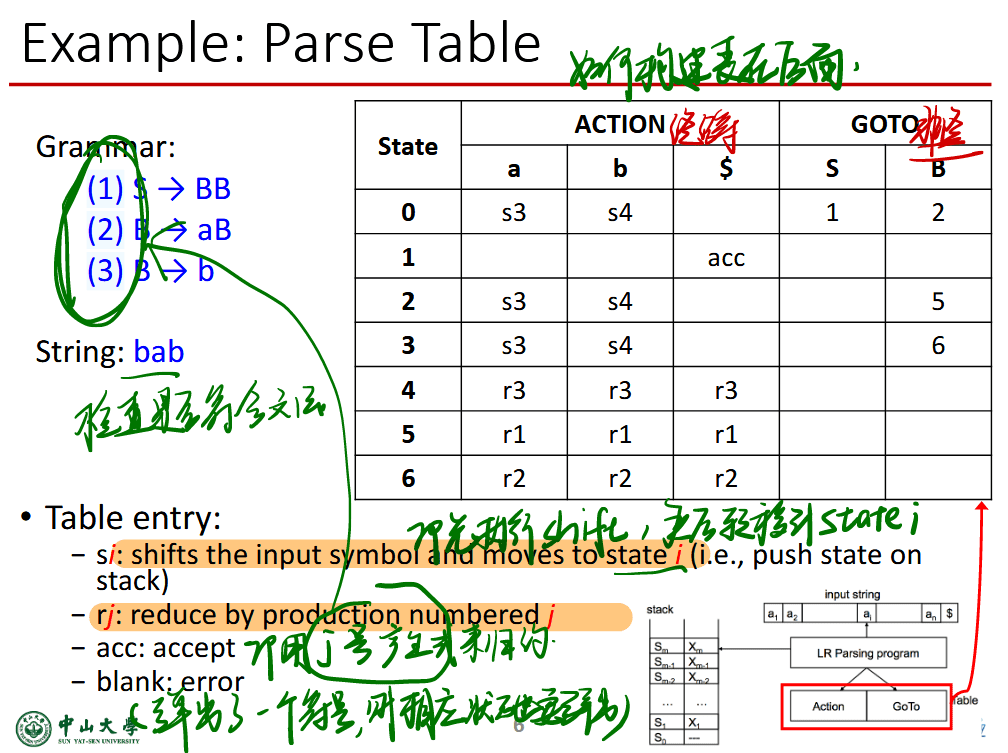
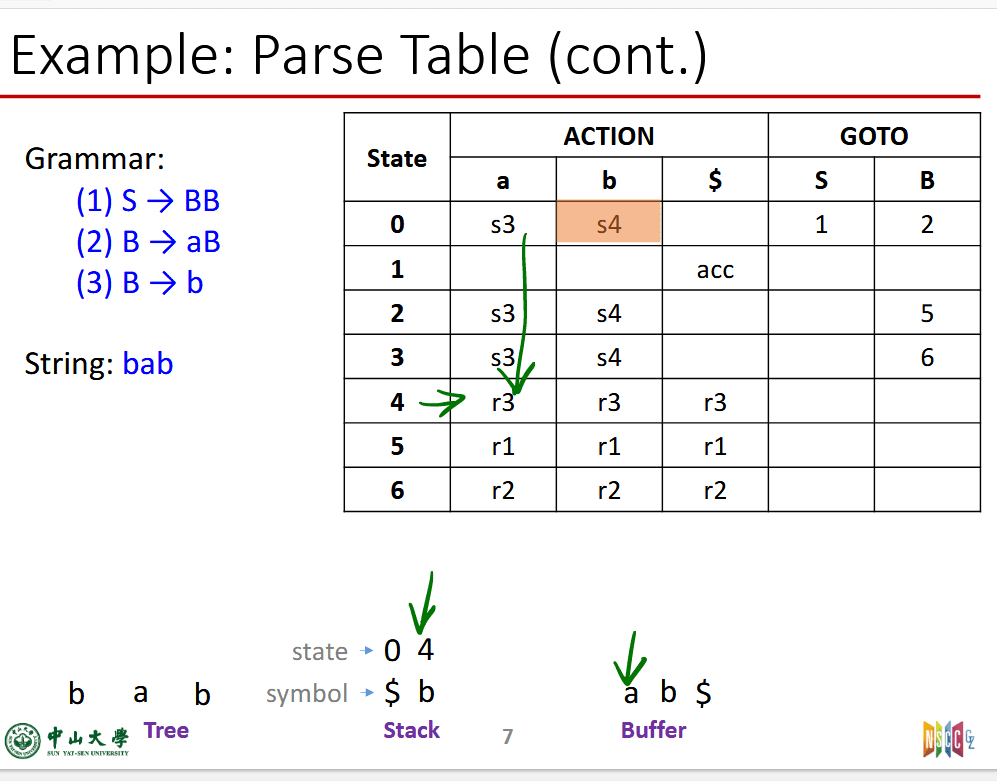
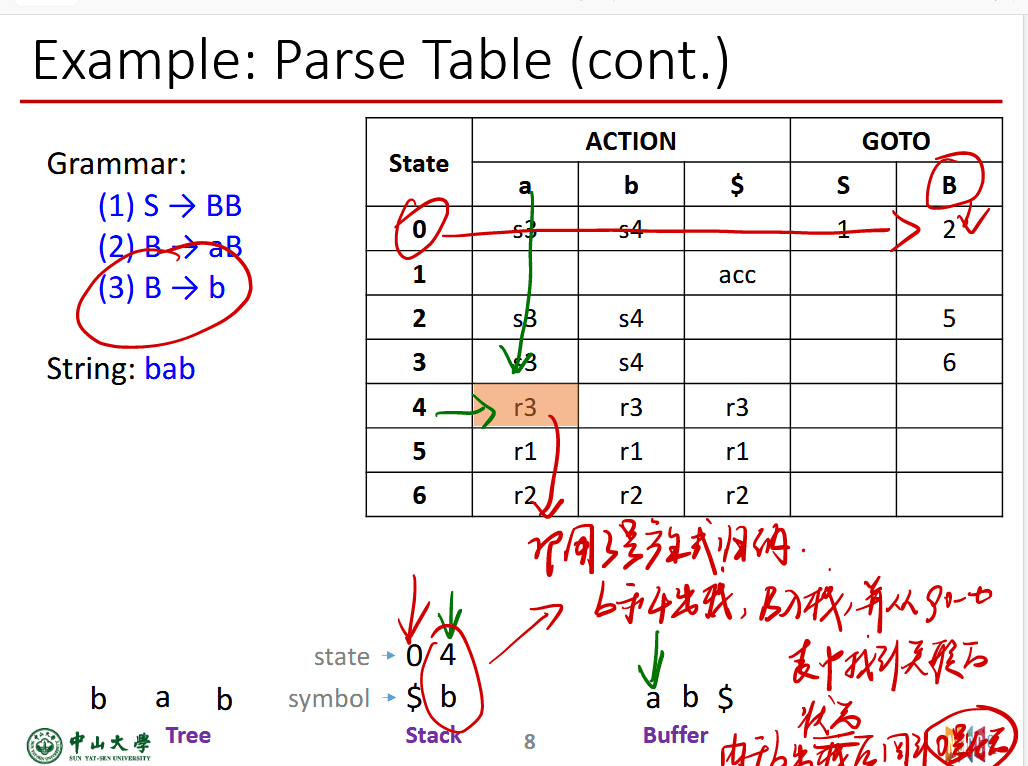
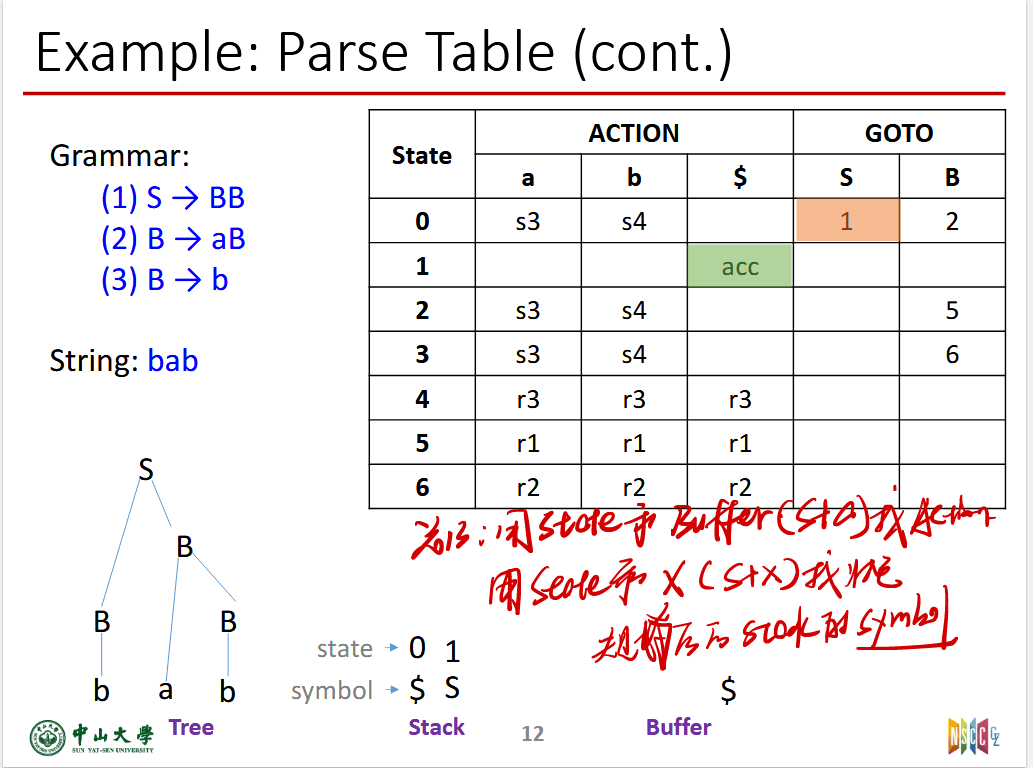
如何使用解析表
PPT:lec11
表条目的意思:
- si:及先执行shift,然后转移到 state i
- rj:用j号产生式来归约,规约之后要去goto表找对应状态加到stack中
- ACC:接受
- 空白:错误
最终目标是栈中只有$
如何构建解析表
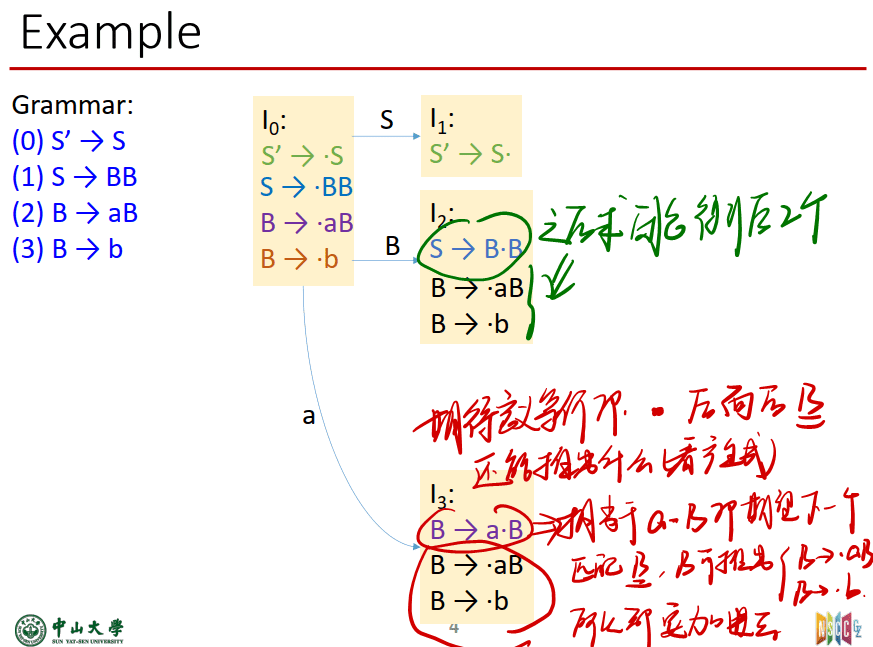
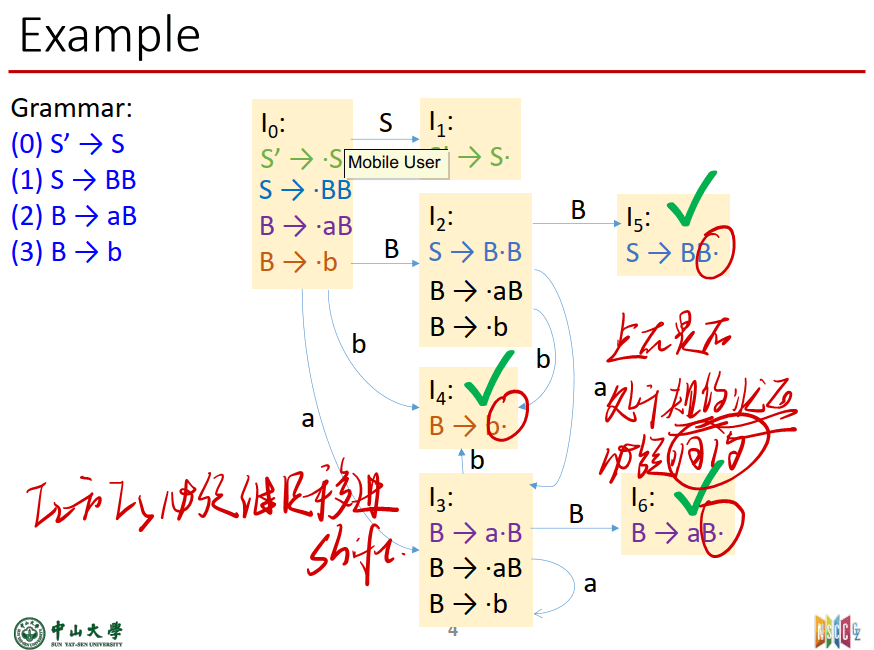
- 求出item(根据增广文法求)
- 由S’->S求出I0(这里需要用到求closure的方法,每一个$I_{k}$都是先根据$I_{k-1}$中的item,找到转移symbol可得到的下一个状态的item,然后看点后面的符号,在全部的production中找到可以的符号再加入到$I_{k}$中)
- 然后一步步求出全部的I得到DFA
- 根据DFA构建ACTION表和GOTO表
增广文法
| 首先引入,增广文法的概念,这个比较简单。G的增广文法G’是 G加上一个新的 开始符S’,并且加入产生式 :$ S’->S$ (S为G的开始符) 得到的文法。其目的是告诉语法分析器合适结束(当要运行规则$ S’->S $时结束),==同时还要把同时又多个可能的拆开,例如$S \to AB | a$ 拆为 $S \to AB, S \to a$== |
对文法进行增广的目的是为了区分开某些右部含有开始符号的文法,在归约过程中能分清是否已归约到文法的最初开始符,还是在文法右部出现的开始符号,增广文法的开始符号S′只在左部出现,这样确保了不会混淆。
也就是添加了一个0号规则保证ACC的唯一性
S0 initial state
也就是加入了增广文法之后的item set
例子: \(S \to AB | a\\ A \to a | ε \\ B \to b\) 那么initial stage $S_0$是: \({ S’\to .S, S \to .AB, S \to .a, A \to .a, A \to . }\)
下面介绍具体实现,构造LR语法分析器的关键就在于 识别 何时该 移入,何时该规约。
LR语法分析器通过维护一些状态,来做出 移入-规约 决策。
那么这些状态是什么? 是 item 的集合。
如何求文法的项目item
那么 item 是什么?:一个文法G的LR(0)item(简称item)是G的一个产生式再加上位于其中的某点,比如,
- $A->XYZ $有4个item:
- $A->\epsilon$ 只有一个item:
item的通俗理解是: 表明了在语法分析 过程中 ,我们已经看到了 一个产生式的哪些部分
举例来说:
- $A->\dot\ XYZ $在接下来的输入中期望看到从$XYZ$推导而得到的串
- $A->X\dot\ YZ $表明我们刚刚在输入中看到了一个可以由$X$推导得到的串,并且希望看到从$YZ$推导得到的串。
- $A->XYZ \dot\ $表示已经看到了产生式体 $XYZ $可以,可以执行规约了。
==如何求项目:如何求项目:就给每个规则加一个点以后然后挪位置,挪一个位置就得到一个项目,操作完了以后你就得到了一堆项目==
item的集合叫LR parser的configuration set[配置集]
根据项集族,可以构建 DFA(确定有穷自动机) -> 利用该自动机,就可以自动作出决策(移入 or 规约)
明确来说,自动机的每个状态对应item set族中的一个item set,
下面来研究如何 构造LR(0)的项集族。
- 项就是上文的item,已经有明确定义
- item set或者项集,表示 item的集合,
- item set族或者项集族,意思就是集合的集合 。
DFA的每个状态对应 LR(0)项集族中的一个元素,也就是一个项集
项目集闭包(closure of item sets)
也是期待意义等价
求闭包是要先根据$I_{k-1}$得到$I_k$(对应到图里面,走横线上的才看上一个框),然后对$I_k$中的item求闭包(求闭包的时候(用点后面那个符号扩展继续推)要看所有的产生式。)
下面引入 项集的闭包的概念
如果I是文法G的一个项集,那么$ CLOSURE(I) $通过以下算法生成:
-
令其为$I$(也就是把$I$中每一项都会被加到$ CLOSURE(I) $中 ) ;
-
如果 $A\to\alpha \dot\ B\beta $位于$CLOSURE(I)$ 中,且 $B\to\gamma $是一个产生式,将$ B\to\dot\ \gamma $加入$CLOSURE(I)$(如果有了就不加)
也就是点后面的那个符号还能推出什么(这一步要查看所有产生式),都加到$ CLOSURE(I) $中
-
不断应用规则2,直到没有新项可以加入$CLOUSURE(I)$.
对应到图里面,走横线上的才看上一个框,求闭包的时候(用点后面那个符号扩展继续推)要看所有的产生式。
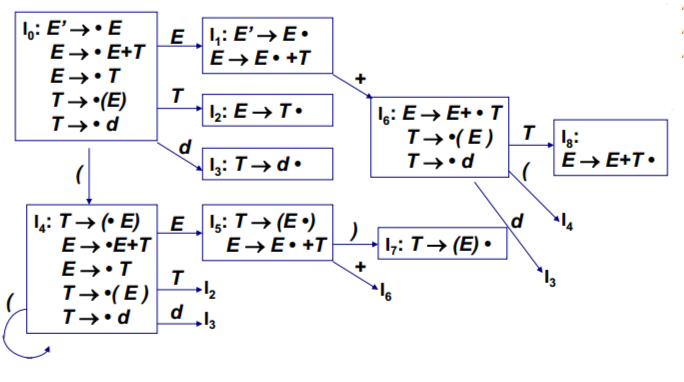
例子1:已知文法G[E]如下: (1) E -> E+T (2) E -> T (3) T ->( E ) (4) T -> d
可以直到它的拓广文法G’ [E’]为 : (0) E’ -> E (1) E -> E+T (2) E -> T (3) T -> ( E ) (4) T -> d
令I0 = CLOSURE({E’->.E})
则I0 = { E’ -> • E,(这一步是根据{E’->• E}得到的)
剩下这些是求闭包产生的,要看全部产生式
E -> • E+T, E -> • T, T -> •( E ), T -> • d }
例子2:
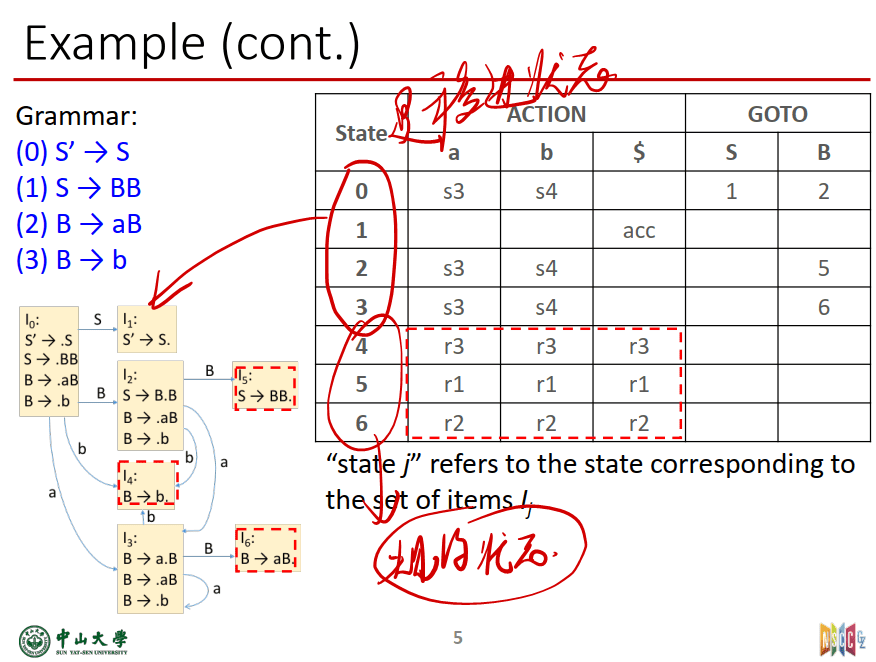
表条目的意思:
- si:及先执行shift,然后转移到 state i
- rj:用j号产生式来归约
- ACC:接受
- 空白:错误
最终目标是栈中只有$
在实际工程实践中,分两种项,
1)核心项: 包含初始项 $S’\to\dot\ S $以及点不在最左端的所有项
2)非核心项: 除了 $S’\to\dot\ S $之外的点在最左端的所有项
由于,我们感兴趣的(也就是实际中能出现)的每一个项集 都是某个内核项的闭包,则如果抛弃非内核项,就可以用很少的内存来表示项集
【注:以上的意思就是,实际工程出现的项集都是内核项集的闭包, 所以只需要用内核项集来表示 真实项集(节省内存),需要的时候执行一次闭包运算即可】
Goto函数(状态转移函数)
下面引入 GOTO函数 的概念
GOTO (I,X) = CLOSURE(J)
GOTO(I,X):返回可以通过推进X到达的状态。
GOTO(I,X) 输入I 为项集 ,X为语法符号。其取值为是一个项集,定义为:
I中所有形如 $[A\to\alpha\dot\ X\beta] $的项【这里括号只是强调是一个项】所对应的项$[A\to\alpha X\dot\ \beta] $的集合的闭包 。
也就是先归约/识别之后再求闭包,表示对于一个状态项目集中的一个项目A -> α• Xβ,在下一个输入字符是X的情况下,一定到另一个新状态 A -> αX•β。
例如:
(0) E’ -> E (1) E -> E+T (2) E -> T (3) T -> ( E ) (4) T -> d
那么$GOTO(I_0,E)=CLOSURE{E’ -> E \cdot ,E -> E\cdot+T}$
显然,GOTO定义了DFA的转换关系。自动机的状态对应于项目集,goto(I, X)指定输入 X 下 I 的状态转换
有了以上概念,我们可以来构造增广语法G’的 LR(0)项集族C了(实际就是构建DFA)
例子:
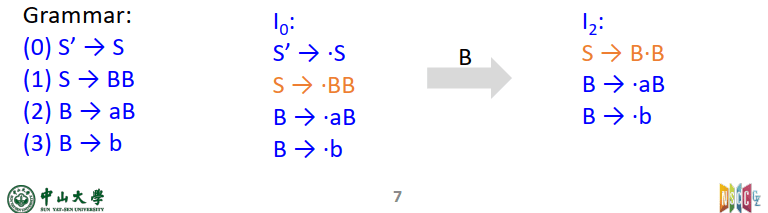
算法如下:
1
2
3
4
5
6
7
8
9
void items(G') {
C={CLOSURE({[S'->.S]})};
repeat
for (C中的每个项集I)
for(每个文法符号X)
if(GOTO(I,X)非空 且不在 C中)
将GOTO(I,X)加入 C中;
until 在某一轮中没有新 项集 被加入 C
}
LR(0) 有限状态机的构造
从 LR(0) FSM 的初态出发 ,先求出初态项目集的闭包(CLOSURE({S’->.S})),然后应用上述转移函数,通过项目分析每种输入字符下的状态转移,若为新状态,则就求出新状态下的项目集的闭包,可逐步构造出完整的 LR(0) FSM。
LR(0) FSM 的构造举例 给定文法G[E]: (1) E -> E+T (2) E -> T (3) T -> ( E ) (4) T -> d
构造LR(0) FSM ① G[E]的拓广文法,得到G’ [E’]: (0) E’ -> E (1) E -> E+T (2) E -> T (3) T -> ( E ) (4) T -> d
②构造G’[E’] 的 LR(0) FSM
LR(0) 有限状态机的构造方法
- 用闭包函数(CLOSURE)来求DFA一个状态的项目集
- 求LR(0) FSM 的状态转移函数GOTO函数
- LR(0) 有限状态机的构造
LR(0)分析表的构造
ACTION 表项和 GOTO表项可按如下方法构造:
a 为终结符,A为非终结符
- 若项目$A ->α • aβ$属于 $I_k$ 且 $GO (I_k, a)= I_j$, 期望字符a 为终结符,则置$ACTION[k, a] =sj $(j表示新状态的下标/状态号);
- 若项目$A ->α • Aβ属于 I_k$,且$GO (I_k, A)= I_j$,期望字符 A为非终结符,则置$GOTO(k, A)=j$ (j就是下一个状态的下标/状态号)
- 若项目$A ->α •$属于$I_k$, 那么对任何终结符a, 置$ACTION[k, a]=rj$;其中,假定$A->α$为文法G 的第j个产生式;
- 若项目$S’ ->S • $属于$I_k$, 则置$ACTION[k, #]$为“acc”;
- 分析表中凡不能用上述规则填入信息的空白格均置上“出错标志”
用人话说就是:
- 不是句柄且栈顶为终结符:如果圆点不在项目k最后且圆点后的期待字符a为终结符,则ACTION[k, a] =sj (j表示新状态Ij);
- 不是句柄且栈顶为非终结符:如果圆点不在项目k最后且圆点后的期待字符A为非终结符,则GOTO(k, A)=j (j表示文法中第j个产生式);
- 是句柄则归约:如果圆点在项目k最后且k不是S’ ->S,那么对==所有==终结符a,ACTION[k, a]=rj (j表示文法中第j个产生式);
- 如果圆点在项目k最后且k是S’ ->S,则ACTION[k, #]为“acc”;
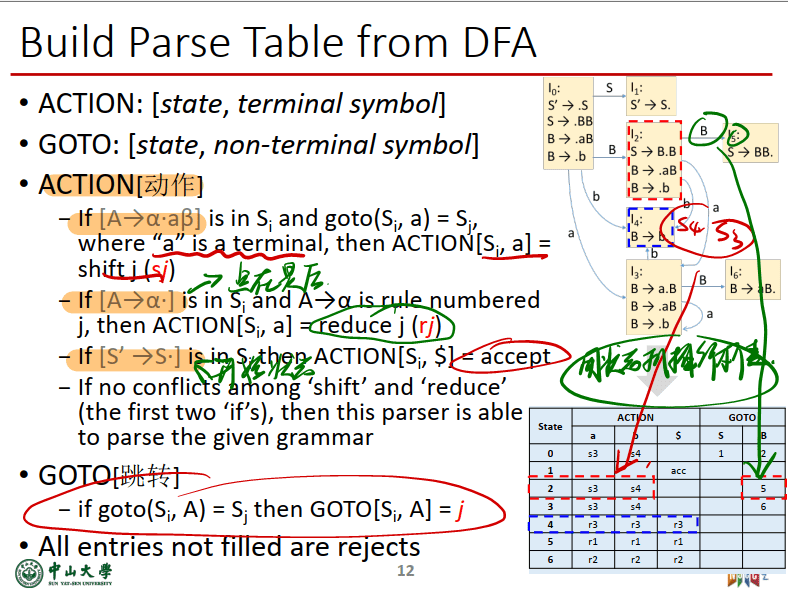
例子:
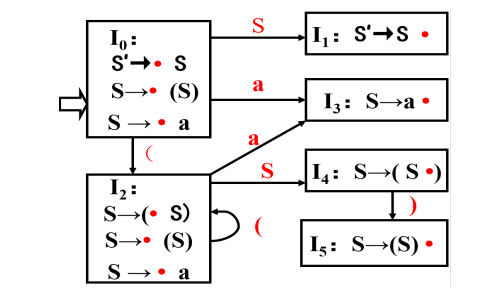
考虑文法G[S] : S → (S) | a
相应的LR(0) FSM如下,构造其LR(0)分析表。
LR(0) FSM
从I0看,
- $S’->·S$,期望字符是非终结符S,根据上面的规则2,得到GOTO(0,S)=1;
- $S->·(S)$,期望字符是终结符( ,根据上面的规则1,得到ACTION(0,()=S2;
- $S -> ·a$,期望字符是终结符a,根据上面规则1,得到ACTION(0,a) = S3
从I1看
- $S’->S·$,根据规则4,置ACTION[1, #]为“acc”;
从I2看,
- $S->(·S)$,期望字符是非终结符S,根据上面的规则2,得到GOTO(1,S)=4;
- $S->·(S)$,期望字符是终结符( ,根据上面的规则1,得到ACTION(0,()=S2;
- $S -> ·a$,期望字符是终结符a,根据上面规则1,得到ACTION(0,a) = S3
从I3看,
- $S->a·$,根据规则3,置ACTION[3, a]为r2;
从I4看
- $S->(S·)$,期望字符是终结符) ,根据上面的规则1,得到ACTION(0,))=S5;
从I5看
- $S->(S)·$,根据规则3,置ACTION[5, )]为r1;
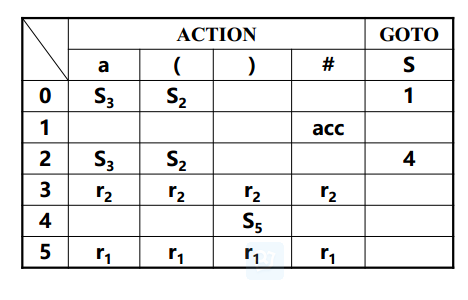
看完所有$I$和里面的所有item,即可得到下表
例子2:


==如何使用LR(0) 的parser table==
shift
reduce
SLR(Simple LR )
LR(0)文法的要求是
- 不同时含有移进项目和归约项目,即不存在移进-归约冲突 。
- 不含有两个以上归约项目,即不存在归约-归约冲突。
例如项目集$Ii$中存在: Ii ={A->α•bγ , B→ γ•,C→β• },此时就同时存在移进-归约冲突和归约-归约;因为你不知道下一步是选择归约还是移进,选择归约的话选择哪个产生式归约。
而事实上一般文法满足这种要求有一定难度,但是假如在归约时出现了移进-归约冲突或者归约-归约冲突,我们可以通过在待分析的字符串中向后再看一位,大多数情况下通过这一位字符就可以确定,选择哪一个表达式归约,或是移进操作。
这种方法就叫做SLR(1)分析法,即简单的LR(1)分析法。
如何判断能否用SLR(1)解决冲突
假如LR(0) 项目集规范族中有项目集 Ii 含有移进-归约冲突和归约-归约冲突: Ii ={A1->α1•b1γ1 ,… , Am->m•bm γm, B1->β 1 • ,…, Bn-> β n • },若集合{b1 ,b2,… ,bm }、FOLLOW(B1) 、 FOLLOW(B2) ,…,FOLLOW(Bn)均两两不相交,则可用SLR(1)解决方法解决分析表上第i行上的冲突问题。
如何构建SLR(1)的表
与LR(0)相比表的结构一致但是动作填充不同,只有下一个token再FOLLOW集中才归约:
假设下一个移进的字符为b,
- 若
b∈ {b1 ,b2,… ,bm },则移进输入符; - 若
b∈FOLLOW(Bj) ,j=1 ,… ,n,则用Bj-> βj归约;
综上,我们可以在构建分析表时做出如下改变(只有填rj时才有变化):
-
若项目
A ->α • aβ属于 $I_k $且GO (Ik, a)= Ij,期望字符a 为终结符,则置ACTION[k, a] =sj(j表示新状态Ij); -
若项目
A ->α • Aβ属于 $I_k $,且GO (Ik, A)= Ij,期望字符 A为非终结符,则置GOTO(k, A)=j -
==若项目
A ->α •属于$I_k $, 那么对任何终结符a,只有满足a属于follow(A)时,才 置ACTION[k, a]=rj;其中,假定A->α为文法G 的第j个产生式;==LR(0)中是不管怎么样,全部终结符a都有ACTION[k, a]=rj,这里是只有满足a属于follow(A)时才可以置ACTION[k, a]=rj
-
若项目
S’ ->S •属于$I_k $, 则置ACTION[k, #]=“acc”; -
分析表中凡不能用上述规则填入信息的空白格均置上“出错标志”
SLR(1)分析的例子
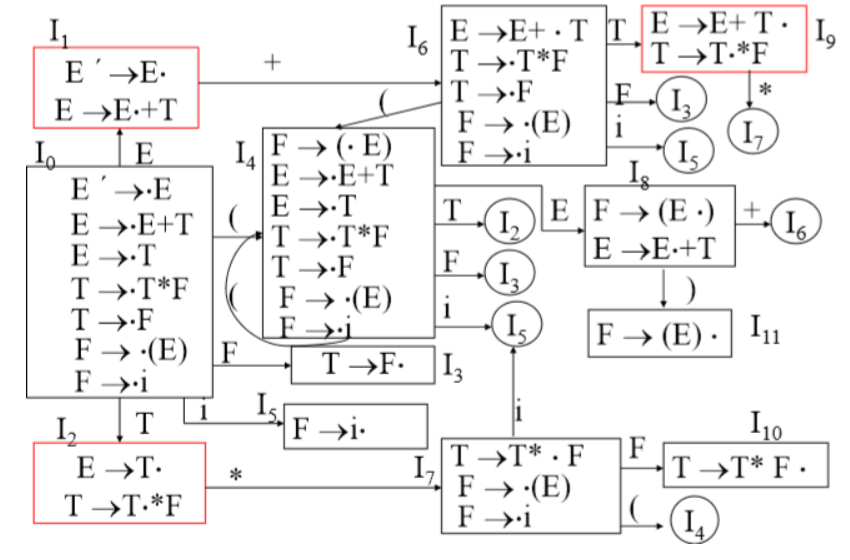
算术表达式文法G[E]: E→E +T | T T→T * F | F F→ (E)| i 求此文法的识别规范句型活前缀的DFA,分析句子i+i *i。
- 将文法拓广为G’[E’]: (0) E’ ->E (1) E-> E +T (2) E ->T (3) T ->T * F (4) T ->F (5) F ->(E) (6) F ->i
- 构造识别规范句型活前缀的DFA
DFA
-
判断有无冲突:
I1 ,I2 ,I9有移进_归约冲突。 I1:E´ ->E· E ->E·+T I2: E ->T · T ->T · *F I9: E ->E+T· T ->T · *F
-
==考虑能否用SLR(1)方法解决冲突:==
对于I1:
{ E´ ->E· E ->E·+T}因为:{+} ∩ FOLLOW(E´)= {+} ∩ {#} =∅, 所以可用SLR(1)方法 解决I1的冲突。对于I2:
{E ->T· T ->T·*F}因为:{*} ∩ FOLLOW(E)= {*} ∩ {#,),+} = ∅所以可用SLR(1)方法解决I2的冲突。对于I9:
{E ->E+T· T ->T ·*F}因为:{*} ∩ FOLLOW(E)= ∅, 所以可用SLR(1)方法解决I9的冲突。 -
构建分析表:
分析表
6.句子i+i *i的分析过程:
| 步骤 | 状态栈 | 符号栈 | 输入符 | 剩余输入串 | 查表 | 操作 |
|---|---|---|---|---|---|---|
| 1 | 0 | # | i | i+i*i# | Action[0,i]=S5 | 移进i |
| 2 | 0 5 | # i | + | +i*i# | Action[5,+]=r6,GOTO(0,F)=3 | 用F -> i 归约 |
| 3 | 0 3 | # F | + | +i*i# | Action[3,+]=r4,GOTO(0,T)=2 | 用F -> T归约 |
| 4 | 0 2 | # T | + | +i*i# | Action[2,+]=r4,GOTO(0,E)=1 | 用F -> E归约 |
| 5 | 0 1 | # E | + | +i*i# | Action[1,+]=S6 | 移进+ |
| 6 | 0 1 6 | # E + | i | i*i# | Action[6,i]=S6 | 移进+ |
| 7 | 0 1 6 5 | # E + i | * | *i# | Action[5,*]=r6,GOTO(6,F)=3 | 用F -> i 归约 |
| 8 | 0 1 6 3 | # E + F | * | *i# | Action[3,*]=r6,GOTO(6,T)=9 | 用F -> F 归约 |
| 9 | 0 1 6 9 | # E + T | * | *i# | Action[9,*]=S7 | 移进* |
| 10 | 0 1 6 9 7 | # E + T * | i | i# | Action[7,i]=S5 | 移进i |
| 11 | 0 1 6 9 7 5 | # E + T * i | # | # | Action[5,#]=r6,GOTO(7,F)=10 | 用F -> i 归约 |
| 12 | 0 1 6 9 7 10 | # E + T * F | # | # | Action[10,#]=r3,GOTO(6,T)=9 | 用T -> T+F归约 |
| 13 | 0 1 6 9 | # E + T | # | # | Action[9,#]=r1,GOTO(0,E)=1 | 用E -> E+T归约 |
| 14 | 0 1 | # E | # | # | Action[1,#]=acc | 接受 |
LR(1)
SLR(1)的问题
仍有Shift-reduce conflict
无效归约问题:
在SLR(1)分析中,我们考虑了所归约非终结符的 Follow 符号,这可以分析出怎么选择归约或移进,但是在选择归约的情况中里,我们只是确认了移进符号是属于非终结符的Follow集的,而没有确认移进后是否是表达式文法规范句型的活前缀,也就是未考虑非终结符 Follow 集中的符号是否也是句柄的 Follow 符号;这样虽然不会影响判断结果,但产生了无效归约,减低了效率。
例:现在符号栈中的元素是
βα,移进符号是a,已知有归约项目A->α,并且a属于follow(A)而a不属于follow(βα);此时我们的做法是归约然后移进,之后的符号栈中的元素是βAa,而βAa不是文法规范句型的活前缀。如果我们能判断出
a!∈follow(βA),就可以判断出出错了。
局限性问题:
SLR(1)分析的要求是:Ii ={A1->α1•b1γ1 ,… , Am->m•bm γm, B1->β 1 • ,…, Bn-> β n • },若集合{b1 ,b2,… ,bm }、FOLLOW(B1) 、 FOLLOW(B2) ,…,FOLLOW(Bn)均两两不相交。和上面的道理相似,没有考虑非终结符 Follow 集中的符号是否也是句柄的 Follow 符号,导致虽然follow集出现了相交,但是事实上正确的符号串是不会出现某些 follow集中的符号的,从而不能判断。
已知:增广文法 G’ [ S ]: (0) S -> E (1) E -> (L , E ) (2) E -> F (3) L -> L , E (4) L -> E (5) F -> ( F ) (6) F -> d
有G’ [S] 的 LR(0)FSM:
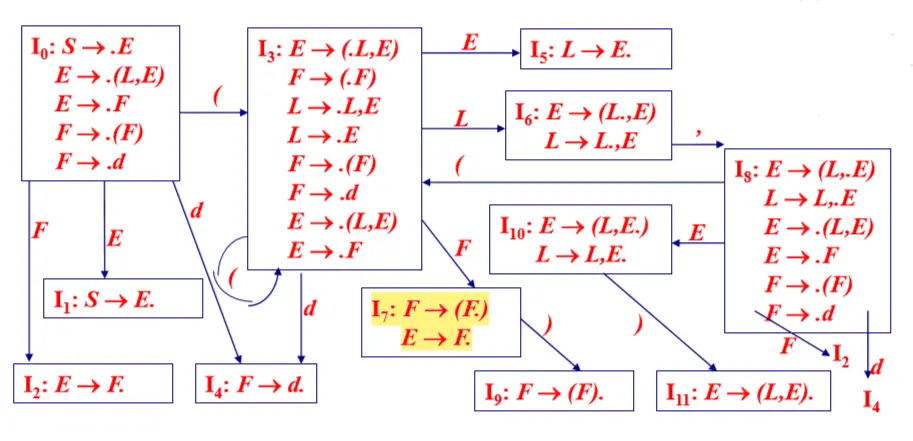
G’ [S] 的 LR(0)FSM
在I7中出现了
{)}∩follow(E)={)}的情况,所以不能进行SLR(1)分析;但是I7中的情况是(·F,E),此时的follow(E)中没有)而应该是,。
LR(1)分析法原理
规范 LR(1) 项
还记得 LR(0) 项长什么样子吗?LR(1) 项和它挺像的。对于某个产生式 𝐴→𝛼𝛽 ,和它对应的其中一个 LR(1) 项就是 [𝐴→𝛼·𝛽,𝑎] ,其中 𝑎 是这个项的向前看符号(lookahead)。如果 LR(1) 中的点号不在项的最右侧,向前看符号没有任何意义;当点号在最右端时,向前看符号表示,只有下一个输入的符号和 𝑎 一致时,我们才归约这个产生式。
我们在求项目集的时候,每个项目的末尾添加一个非终结符$并以,分隔开来,来表示在当前情况下用该产生式进行规约时所期望的下一个字符,称之为向前搜索符,来替代follow集。
首先,明白了在 LR(1) 分析法中展望是为了解决其他分析法解决不了的问题。简单的说就是,状态会出现冲突,我们不能只通过后 1 个输入串符号,直接确定选用哪个产生式,这是严重的错误。
所以 展望(向前搜索符) 是通过展望后面的内容,所以展望对应的终结符,应该 属于该非终结符的 FOLLOW 集(确切的说,属于 FOLLOW 集中的具体哪个个终结符,应该根据产生式的推导过程确定,通过语法树来分析,是比较直观的方法。也可以直接通过求该非终结符后的 FIRST 集来确定,但要注意是对谁求 FIRST 集,可表示为 FIRST(βa),例题中会提到),来帮助唯一确定选择产生式。
拓展注:这里提到的 FOLLOW 集和 FIRST 集不是冲突的,因为我们要求的向前搜索符时 FOLLOW 集的子集,有时候不能确定,所以用 FIRST(βa), β 表示由谁哪个非终结符推导的,这个非终结符的后面的剩余串,a 表示它上一个状态中的向前搜索符。它俩拼接起来的串,对该串求 FIRST 集。 那么可能会有疑问,利用上一个状态?那第一个状态呢?第一个状态是固定的 S’→S,# 其实 # 就是 S 的 FOLLOW 集中的唯一的元素,它也是开始符号的向前搜索符 所以说 FOLLOW 集和 FIRST(βa) 是都可以求的,FIRST(βa) 是准确的向前搜索符,它是 FOLLOW 集的一部分
在 LR(1) 中,用
状态, 终结符 例如:S’ → # (#表示开始符号FOLLOW集会提到那个符号,有的地方用 $,是一样的 )
这种形式是表式展望,终结符就是展望的后面的终结符,具体的下面例题中还会提到。
在检查是否可用.LR(1)分析法的时候,要求是Ii={A1->α1•b1 γ1,a1,… , Am->m•bm γm,am , B1->β 1 •,c1,…,Bn-> β n •,cn },若集合{b1} ,{b2},… ,{bm}、{c1} ,{c2},… ,{cm}均两两不相交。满足这样要求的文法称之为LR(1)文法:。
通过比较``{b1},{b2},… ,{bm}、{c1},{c2},… ,{cm}`和待移进字符就能分析出当前应该进行的操作。
如何求LR(1)的Closure(也就是求I)

tips:走横线上过去的,逗号后面都是直接加展望符$,只有求闭包的时候才需要求First集
并且是来自谁就求谁的first(va)
例如上图中$S\to\cdot XX$是由$S’\to\cdot S$推出来的,那么就是First(ε$)=$
$X\to\cdot aX$和$X\to\cdot b$来自$S\to\cdot XX$,那么就是First(X$)=a/b
这里求连续多个的first集时,就是要找到第一个不能推出空的符号才停,然后累加之前所有符号的first集(与求first集一样)
例:增广文法 G’ [ S ]: (0) S -> E (1) E -> (L , E ) (2) E -> F (3) L -> L , E (4) L -> E (5) F -> ( F ) (6) F -> d
构造增广文法G’ [S] 的 LR(1)FSM:
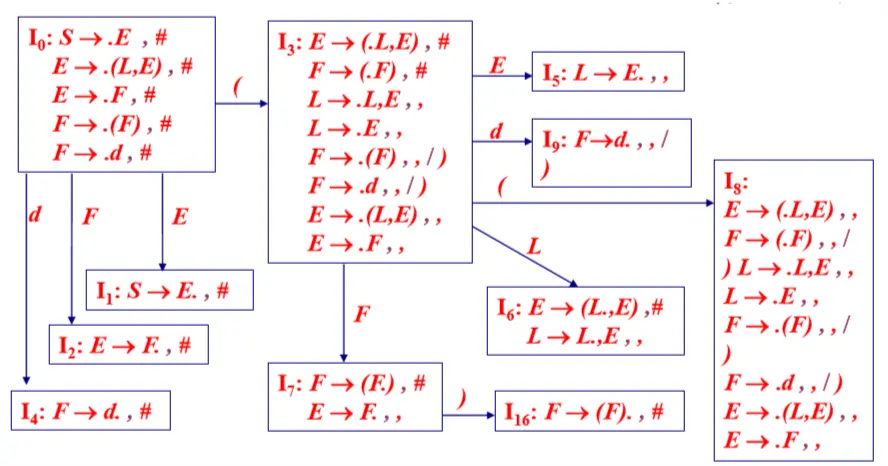
G’ [S] 的 LR(1)FSM(1)
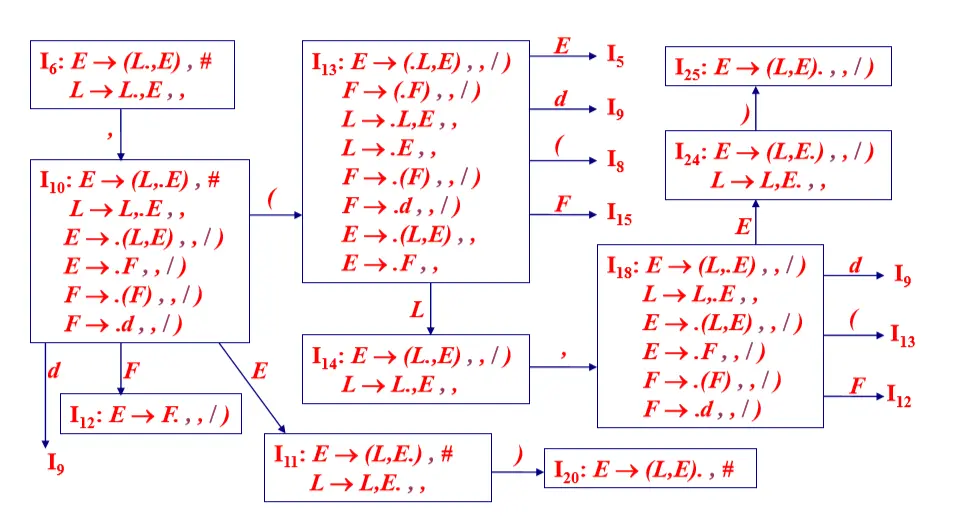
G’ [S] 的 LR(1)FSM(2)
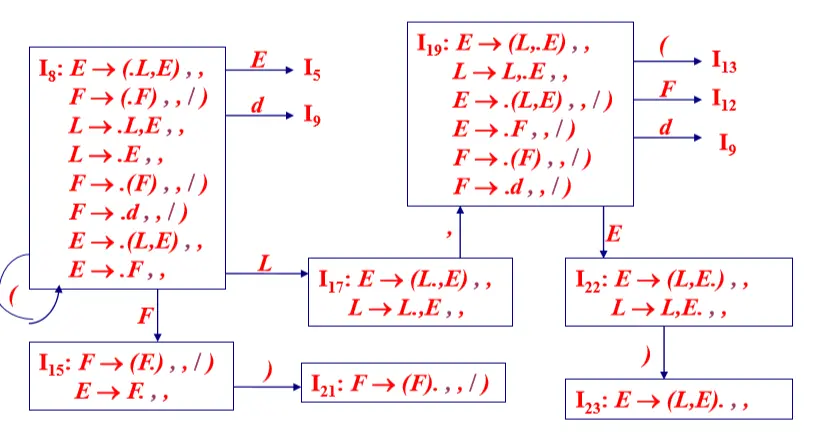
G’ [S] 的 LR(1)FSM(3)
LR(1)构建表
只有r的填写不同,只写到展望的符号的格子中
LR(k)分析
同理可推广到LR(k)分析:
形如: [A ->α . β , a1a2…ak ],其中a1a2…ak 为向前搜索符号串。
移进项目形如:[ A ->α . aβ, a1 a2 … ak] ;待约项目形如:[A ->α . Bβ, a1 a2 … ak]; 归约项目形如:[A ->α . ,a1 a2 … ak] 。
但LR(k)分析只有理论意义,因为LR(1)FSM 的状态数已经很大,k>1 的情形难以想象。
LALR(1)分析(会引入RR冲突)
lec_14-split
LALR是Lookahead LR,是LR(1)和SLR(1)的折中
合并LR(1)中的相似状态(相似状态是:core相同,展望不同,展望就是LR(1)新加入的逗号后的部分,需要根据first集来求的)
LALR的特点是FSM形式上与LR(1)相同,大小上与LR(0)/SLR相当,分析能力介于SLR和LR(1)二者之间 \(SLR<LALR(1)<LR(1)\) 合并后的展望符集合仍为FOLLOW集的子集,LALR相对于LR(1)会延迟错误的发现,因此其分析能力会低于LR(1)分析法。但其对信息的划分比SLR分析法更细致,因此它延迟发生的错误要比SLR分析要少分析能力也就比SLR分析要强。
1.基本概念
-
LR(1)项目的“心”(core):
LR(1)项目
[A -> α . β , a]中的A -> α . β部分称为该项目的“心“ 。 -
同心集:
-
对于LR(1)FSM 的两个状态,如果只考虑每个项目的 “心”,它们是完全相同的项目集合,那么这两个状态互为同心集。
2.LALR(1)分析法原理
我们可以发现LR(1)分析的有限状态机中,项目集的数量十分的多。这是因为许多在LR(0)分析中循环的项目集在LR(1)分析中由于·的位置变化导致向前搜索集也产生了变化,从而产生了许多同心集。而LALR(1)分析法正是对这些同心集进行了合并。
暴风(Brute Force)算法:
- 构造增广文法的 LR(1)FSM 状态 。(FSM=有限状态机)
- 合并“同心”的状态(同心项目的搜索符集合相并) 得到LALR(1) FSM 的状态 。
- LALR(1) FSM 状态由 GO 函数得到的后继状态是所有被合并的“同心”状态的后继状态之并 。
注意:
-
合并同心状态后,不会产生新的移进-归约冲突,但==可能产生新的归约-归约冲突==。
-
一个LR(1)文法,==如果将其LR(1)FSM的 同心状态合并后所得到的新状态无归约-归约 冲突,则该文法是一个 LALR(1)文法 。==
例:增广文法 G’ [ S ]: (0) S -> E (1) E -> (L , E ) (2) E -> F (3) L -> L , E (4) L -> E (5) F -> ( F ) (6) F -> d
构造增广文法G’ [S] 的 LALR(1) FSM
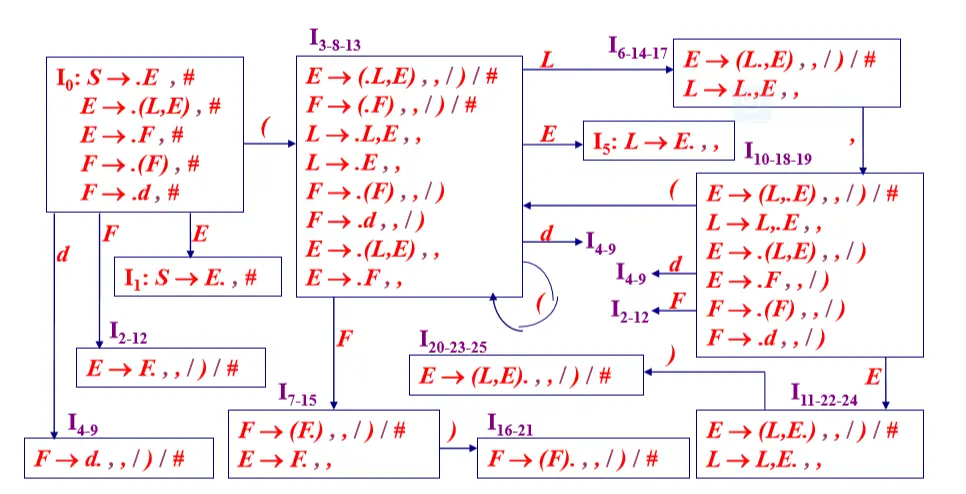
G’ [S] 的 LALR(1) FSM
合并的例子:

(a)
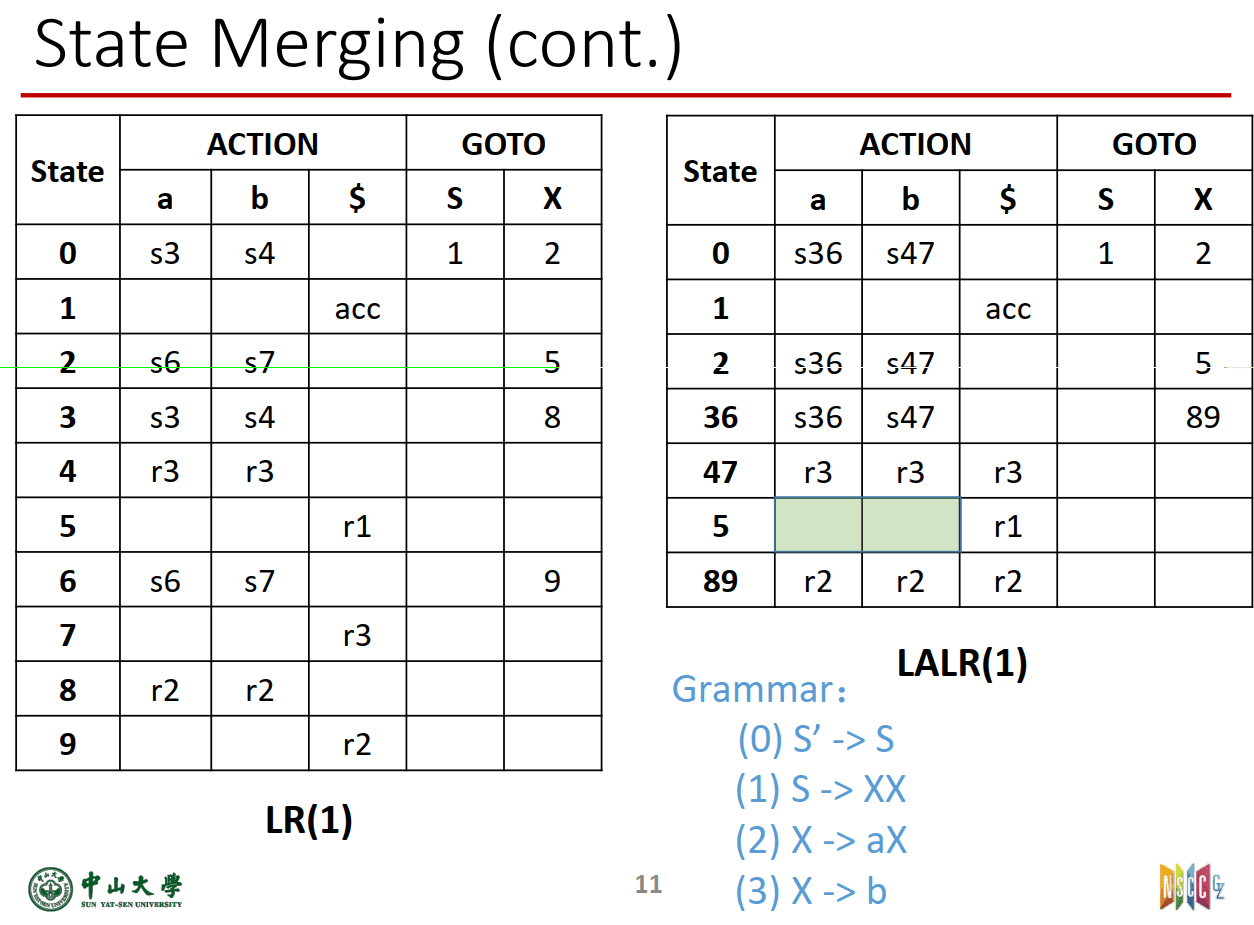
(b)
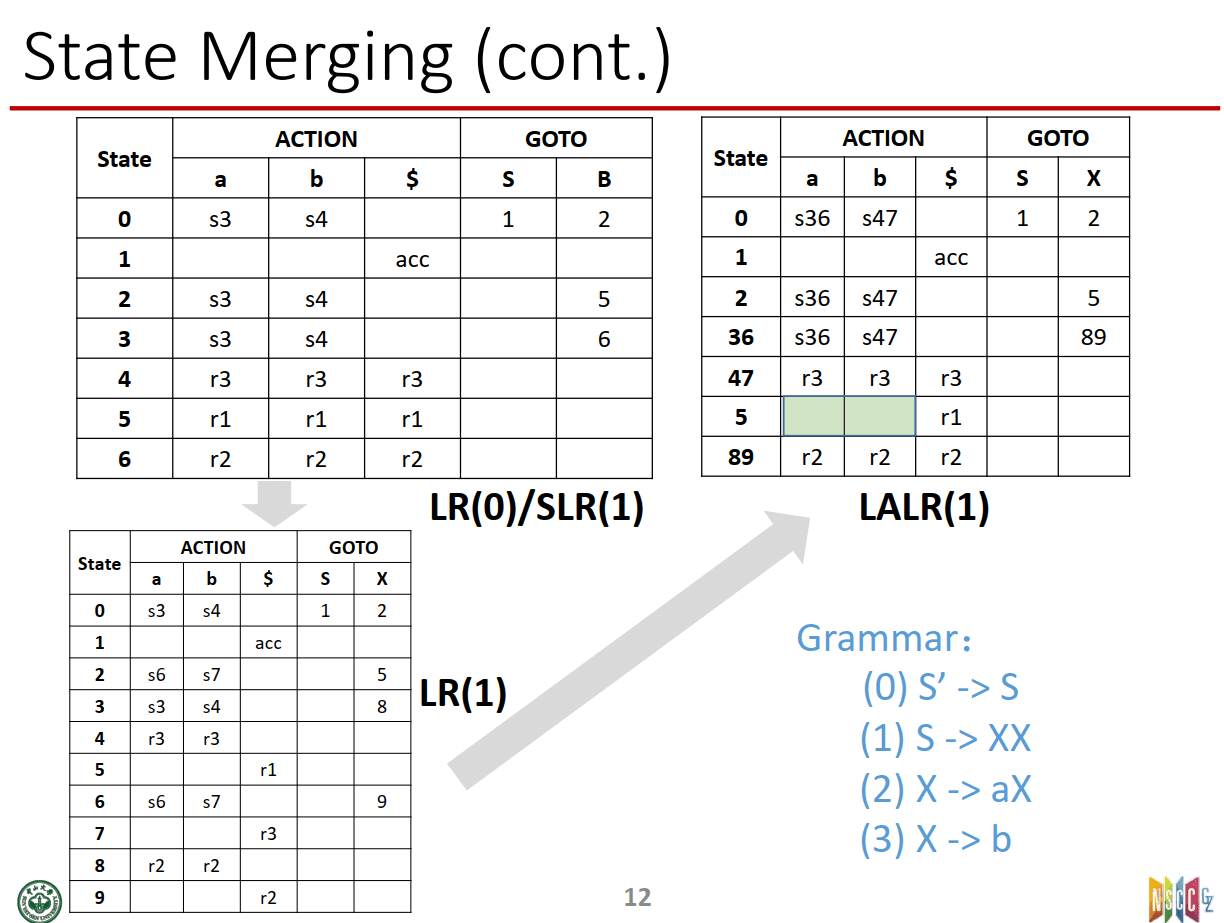
==合并状态后,不会产生新的移进-归约冲突(SR),但可能产生新的归约-归约冲突(RR),只有不产生冲突时才符合LALR(1)==

(a)为什么不会有SR冲突

(b)RR冲突的例子
虽然合并同心项目可能会产生归约-归约冲突,但不会产生移入-归约冲突,是因为同心项目集在合并时只是合并展望符集合,而展望符只在归约时起作用在移入是不起作用的,因此只要合并前项目不存在移入-归约冲突的话合并后也不存在移入-归约冲突。
合并同心项集后,虽然不产生冲突,但可能==会推迟错误的发现==
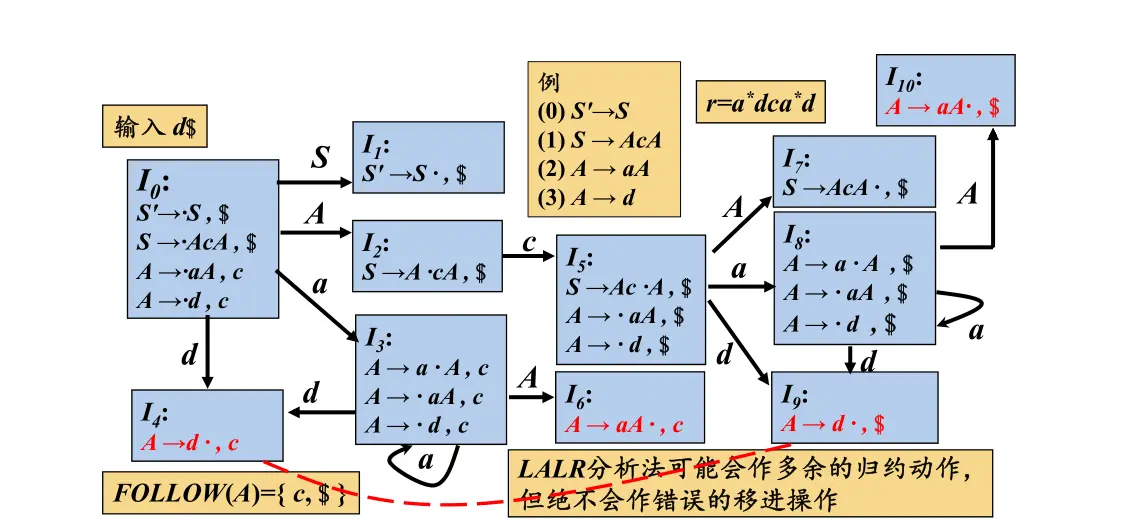
过程:
- 因为状态9合并至状态4,当输入d$时d移入栈后会进入状态4。
- d归约成A后,d跟状态4出栈,A进栈,状态栈露出状态0。
- 0状态遇到A后进入状态2,状态2进栈。
- 接着$进栈,状态2遇到$后报错。
可见如果状态4在跟状态9合并前,在进入状态4前就已经报错。而合并后却进行额外的操作直至进入状态2才报错。可见合并同心项目集后确实推迟了错误的发现。
实际上合并同心项目时合并的其实是对应项的展望符集合,而移入动作与展望符没有任何关系,因此合并展望符集合不会影响移入操作的正确性。
LALR小结

总结
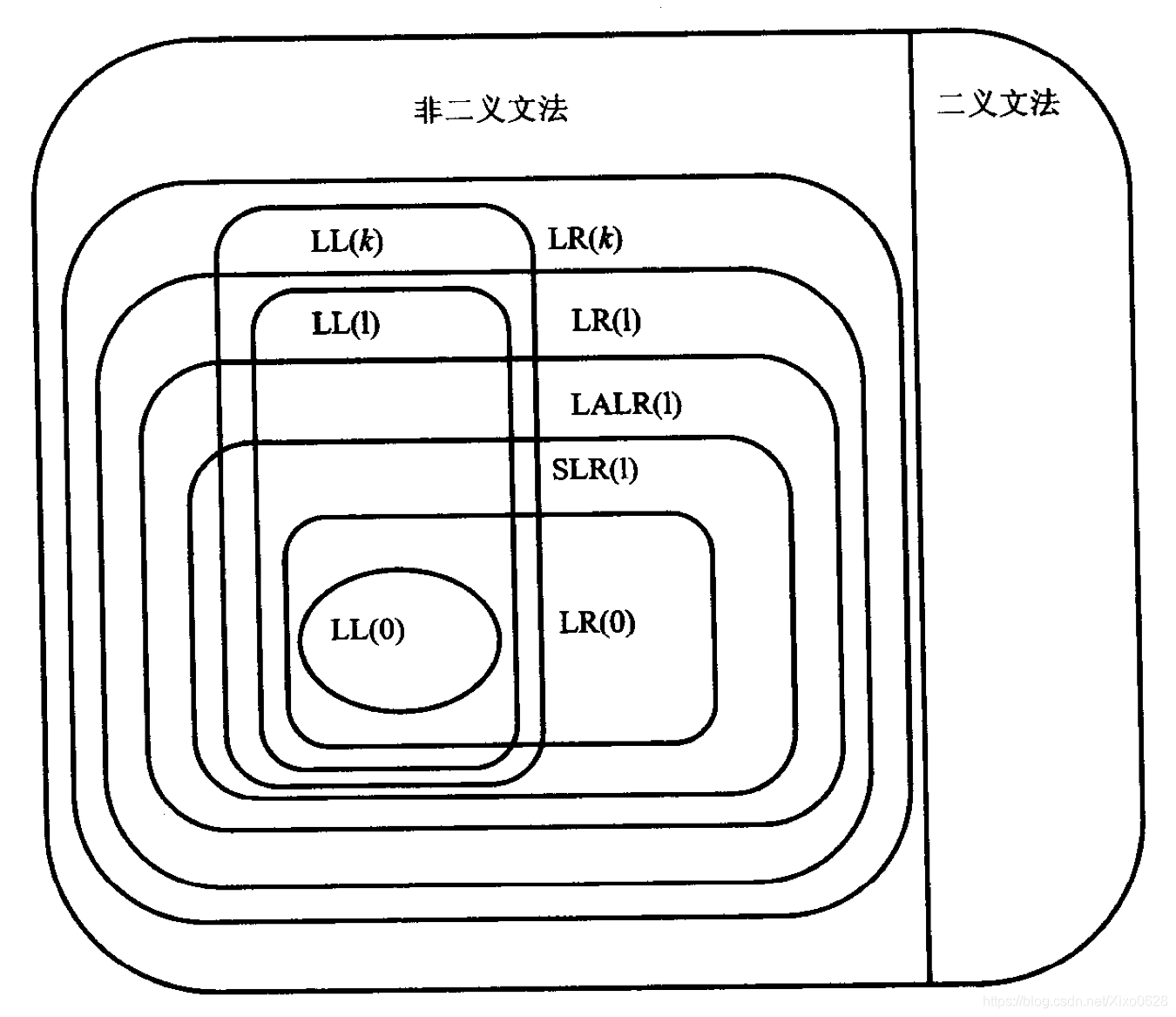
(a)
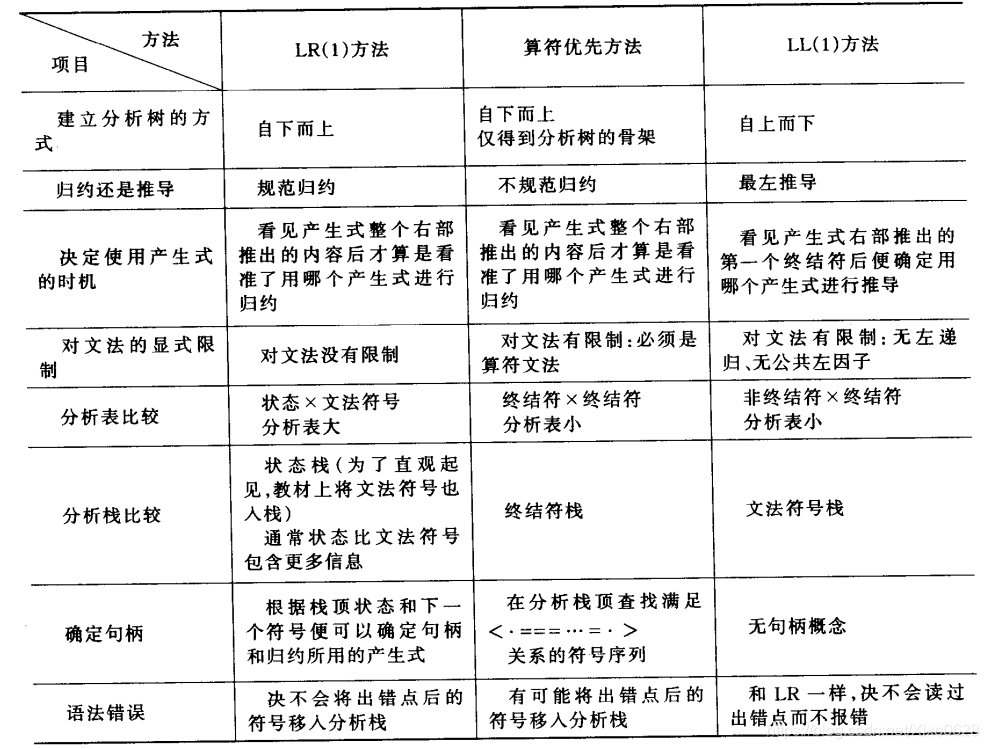
(b)