
Artificial Neural Networks
Final-term Homework:
中-英机器翻译
Student ID: 21307381 Student Name: LJW
Date: 2024.6.22
Lectured by: Xiaojun Quan
Artificial Neural Networks Course
Sun Yat-sen University
实验介绍
数据集简介
数据集说明:压缩包中共有 4 个 jsonl 文件,分别对应着训练集(小)、训练集(大)、验证集和测试集,它们的大小分别是 100k、 10k、 500、 200。 jsonl 文件中的每一行包含一个平行语料样本。模型的性能以测试集的结果为最终标准。
若计算设备受限,可以仅使用训练集(小)中的 10k 平行语料进行训练;鼓励探索使用训练集(大);
数据预处理
数据清洗:非法字符(#,$),稀少字词的过滤;过长句子的过滤或截断。
分词:将输入句子切分为 tokens,每个子串相对有着完整的语义,便于学习 embedding 表达
- 英文: 词语之间存在天然的分隔 (空格、标点符号),可以直接利用 NLTK 或 BPE、 WordPiece (后两个更细粒度)等统计方法分词
- 中文:可以借助分词工具,诸如 Jieba(轻量型), HanLP(大体量但效果好)
构建词典:利用分词后的结果构建统计词典,可以过滤掉出现频次较低的词语,防止词典规模过大
建议用预训练词向量初始化,在训练的过程中允许更新
NMT 模型
- 自行构建基于 GRU 或者 LSTM 的 Seq2Seq 模型 (编码器和解码器各 2 层;单向)
- 自行实现 attention 机制
- 自行探索 attention 机制中不同对齐函数 (dot product,multiplicative, additive) 的影响
训练和推理
-
定义损失函数(例如交叉熵损失)和优化器(例如 Adam)。
- 将双语平行语料库处理成中译英数据,训练模型的中译英能力。
- 在训练过程中,对比 Teacher Forcing 和 Free Running 策略的效果。
- 对比 greedy 和 beam-search 解码策略;
评估指标
BLEU
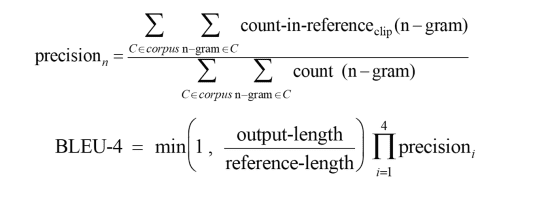
重点考查
-
搭建 Seq2Seq 模型
-
Attention 机制的实现
-
训练 Seq2Seq 模型的技巧
-
分类结果性能评估
-
Attention 可视化(少量案例进行分析)
提交
- 源代码和训练好的 checkpoint
- 文档( PDF)(至少包含方法、实验结果分析以及心得体会)
基础知识
RNN
我们做的大多数决策不只是基于当前获取的信息,也会参考之前存储的先验信息,比如文章、音频和视频都是连续的序列。基于此,我们就不可以使用之前期中使用的卷积神经网络CNN了,因为它的输出只是由当前的输入决定。
这时候就引入了递归神经网络RNN,它是一种专门处理序列信息的具有时间依赖的网络。
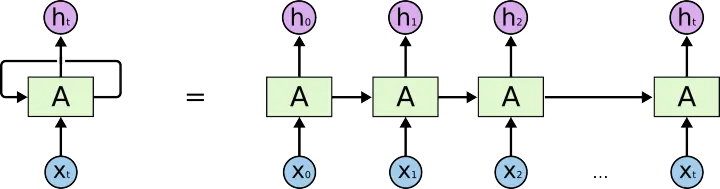
这种链式结构表示了递归神经网络用于序列形式的数据,每一步就输入序列的不同元素,即执行一个cell。序列数据可以是音频(语音识别),文本(翻译)等。而且很明显我们可以看出,输入输出的序列是具有相同的时间长度的,其中的每一个权值都是共享的(不要被链式形状误导,本质上只有一个cell)。
但是RNN存在着梯度消息/爆炸以及对长期信息不敏感(长期依赖)的问题,所以LSTM就被提出来了。
LSTM
在标准的RNN中,这个重复复制的模块只有一个非常简单的结果。
LSTM也有这样的链式结构,但是这个重复的模块和上面RNN重复的模块结构不同:LSTM之所以能够解决RNN的长期依赖问题,是因为LSTM引入了门(gate)机制用于控制特征的流通和损失。包括以下三个门:
- 输出门(output gate)用来从单元中输出条目。
- 输入门(input gate)用来决定何时将数据读入单元。
- 遗忘门(forget gate)用来重置单元的内容,能够通过专用机制决定什么时候记忆或忽略隐状态中的输入。
同时还有一个候选记忆单元。
三个门由三个具有sigmoid激活函数的全连接层处理, 以计算输入门、遗忘门和输出门的值。 因此,这三个门的值都在(0,1)的范围内。候选记忆元使用tanh函数作为激活函数,函数的值范围为(−1,1)。
输入门$𝐼_𝑡$控制采用多少来自候选记忆$\tilde{𝐶}𝑡$的新数据,而遗忘门$𝐹_𝑡$控制保留多少过去的记忆元$𝐶{𝑡−1}$的内容。 使用按元素乘法,得出:
\[𝐶_𝑡=𝐹_𝑡⊙𝐶_{𝑡−1}+𝐼_𝑡⊙\tilde{𝐶}_𝑡.\]如果遗忘门始终为1且输入门始终为0, 则过去的记忆元$𝐶_{𝑡−1} $将随时间被保存并传递到当前时间步。 引入这种设计是为了缓解梯度消失问题, 并更好地捕获序列中的长距离依赖关系。
计算完最右边的$C_t$,接下来需要定义如何计算图中最右边的隐状态 $𝐻_𝑡$, 这就是输出门发挥作用的地方。LSTM中,它仅仅是记忆元的tanh的门控版本。 这就确保了$𝐻_𝑡$的值始终在区间(−1,1)内:
\[𝐻_𝑡=𝑂_𝑡⊙tanh(𝐶_𝑡).\]只要输出门接近1,我们就能够有效地将上一次所有隐状态记忆信息传递给预测部分, 而对于输出门接近0,我们只保留记忆元内的所有信息,而不需要更新隐状态。
GRU
门控循环单元(gated recurrent unit,GRU)是LSTM的简化变体。GRU通常能够提供同等的效果, 并且计算的速度明显更快。
输入是由当前时间步的输入和前一时间步的隐状态
GRU中只有两个门,两个门的输出是由使用sigmoid激活函数的两个全连接层给出:
- 重置门(reset gate):控制“可能还想记住”的过去状态的数量
- 更新门(update gate):控制新状态中有多少个是旧状态的副本
接下来会将重置门$𝑅_𝑡 $与中的常规隐状态更新机制集成, 得到在时间步𝑡的候选隐状态(candidate hidden state) $\tilde{𝐻}_𝑡$。符号⊙表示Hadamard积(按元素乘积),使用tanh非线性激活函数来确保候选隐状态中的值保持在区间(−1,1)中。
\[\tilde{\mathbf{H}}_t=\tanh(\mathbf{X}_t\mathbf{W}_{xh}+(\mathbf{R}_t\odot\mathbf{H}_{t-1})\mathbf{W}_{hh}+\mathbf{b}_h),\]$𝑅_𝑡$和$𝐻_{𝑡−1} $的元素相乘可以减少以往状态的影响。 每当重置门$𝑅_𝑡$中的项接近1时, 也就是普通的RNN网络。 对于重置门$𝑅_𝑡$中所有接近0的项, 候选隐状态是以$𝑋_𝑡$作为输入的多层感知机的结果。 因此,任何预先存在的隐状态都会被重置为默认值。
计算出候选隐状态后就可以根据更新门$𝑍_𝑡$的效果。 就可以进一步确定新的隐状态$H_t$了。这一步确定新的隐状态$𝐻_𝑡$在多大程度上来自旧的状态$𝐻_{𝑡−1}$和 新的候选状态$\tilde{𝐻}𝑡$。 更新门$𝑍_𝑡$仅需要在 $𝐻{𝑡−1}$和$\tilde{𝐻}_𝑡 $之间进行按元素的乘法就可以实现这个目标。 这就得出了门控循环单元的最终更新公式:
\[\mathbf{H}_t=\mathbf{Z}_t\odot\mathbf{H}_{t-1}+(1-\mathbf{Z}_t)\odot\tilde{\mathbf{H}}_t.\]每当更新门$𝑍_𝑡$接近1时,模型就倾向只保留旧状态。 此时,来自$𝑋_𝑡$的信息基本上被忽略, 从而有效地跳过了依赖链条中的时间步𝑡。 相反,当$𝑍_𝑡$接近0时, 新的隐状态$𝐻_𝑡$就会接近候选隐状态$\tilde{𝐻}_𝑡$。 这些设计可以帮助我们处理循环神经网络中的梯度消失问题, 并更好地捕获时间步距离很长的序列的依赖关系。 例如,如果整个子序列的所有时间步的更新门都接近于1, 则无论序列的长度如何,在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。
总结:
- 重置门有助于捕获序列中的短期依赖关系;
- 更新门有助于捕获序列中的长期依赖关系。
Attention
Attention是一种用于提升基于RNN(LSTM或GRU)的Encoder + Decoder模型的效果的的机制。Attention给模型赋予了区分辨别的能力,例如,在机器翻译中,为句子中的每个词赋予不同的权重,使神经网络模型的学习变得更加灵活(soft),同时Attention本身可以做为一种对齐关系,解释翻译输入/输出句子之间的对齐关系,通过Attention可视化即可解释模型到底学到了什么知识。
RNN网络本身缺点:
- RNN具有的梯度消失问题,随着所需翻译句子的长度的增加,这种结构的效果会显著下降。
- RNN结构得到的hidden vector虽然包含了整句话的全部信息,但是这个全部信息具有局部依赖的特性,也就是说越近的句子对hidden vector的贡献越大,很多时候hidden vector其实只学到了每句话最后几个词的信息
- RNN不能够支持并行计算,因为依赖于前一时刻输出,训练起来会很慢,每个词向量对应的导数依赖后续的词的导数,这样递归求导也是梯度消失问题的主要原因。
引入attention机制能够解决前两个问题,self-attention可以解决第三个问题。
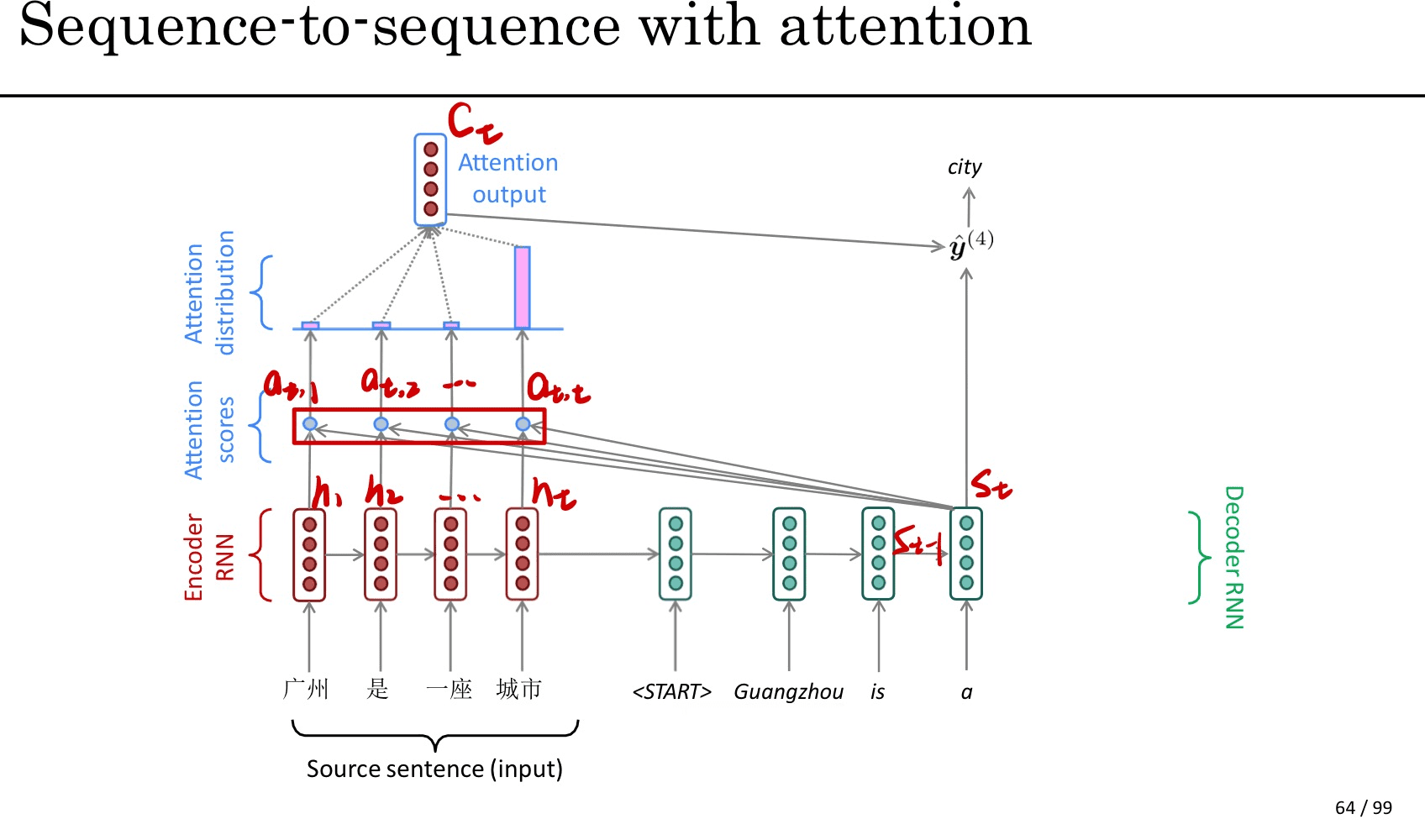
首先我们利用RNN结构得到encoder中的hidden state $h_1$到$h_t$ ,假设当前decoder的hidden state 是$s_{t-1}$,我们可以计算每一个输入位置j的hidden vector与当前输出位置的关联性$similarity(s_{t-1},h_j)$,这个有很多种计算方式,其实就是相似度的计算方式。(也叫对齐函数)
对于所有的$similarity(s_{t-1},h_j)$进行softmax操作后将其normalize得到attention的分布,这一步得到的就是图中的$a_{t,1}$到$a_{t,t}$,也就是decoder的下一层输出与所有输入之间的权重关系。
\[\alpha_{t,j}={e^{similarity(s_{t-1},h_j)}\over{\sum_{k=1}^{T}e^{similarity(s_{t-1},h_k)}}}\]利用$\alpha_{t,j}$我们可以进行加权求和得到相应的context vector $c_t=\sum_{j=1}^{T}\alpha_{t,j}h_j$。
由此,我们可以计算decoder的下一个hidden $s_t=f(s_{t-1},y_{t-1},c_t)$以及该位置的输出$p(y_t\mid y_1,…,y_{t-1},x)=g(y_{i-1},s_t,c_t)$
直观上看,Attention层其实类似于一个非常复杂的全连接神经网络
实验过程
简单介绍
Seq2Seq模型由两个主要的循环神经网络(RNN)组件构成:编码器(encoder)和解码器(decoder)。在机器翻译领域,这两个组件协同工作以实现语言之间的转换。
- 在训练阶段:
encoder接收输入的英文句子,将其分解为一系列的token向量,并按顺序处理这些向量。每个token经过LSTM或GRU单元后,最终在encoder的最后一个时间步生成隐状态( h )和细胞状态( c )。这两个状态随后作为decoder的初始状态。decoder以特定的起始符号SOS为输入,并逐步生成目标语言中的单词序列。每一步生成的单词都作为下一步的输入,同时更新decoder的状态。最终,decoder的输出通过一个全连接层转化为单词的概率分布,该分布与目标句子的one-hot编码形式进行比较,计算损失函数,并据此反向传播更新模型参数。
- 在预测阶段:
预测过程与训练阶段相似,encoder首先处理输入句子并生成最终状态( h )和( c )。这些状态被用作decoder的初始状态。decoder从起始符号开始,根据模型的预测逐步生成单词序列,并将预测的单词作为下一步的输入,以此循环直至生成终止符号,完成翻译序列的输出。
- 引入注意力机制(Attention):
Seq2Seq模型中的注意力机制是对传统模型的重要补充。它允许decoder在每次状态更新时,不仅考虑encoder的最终状态,而是计算与encoder所有时间步的隐状态的相关性。这种机制使得模型能够更加灵活地关注输入序列中的不同部分,从而克服仅依赖最终状态可能带来的信息丢失问题。没有attention机制会只使用encoder的最后时刻的状态来更新decoder的状态,有可能其遗忘掉了在比较靠前的单词的信息。
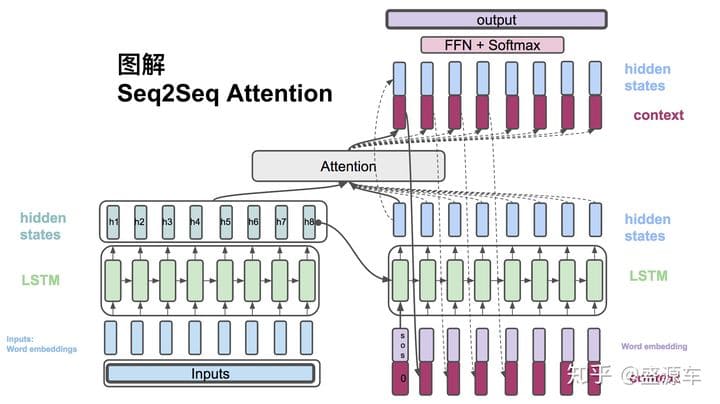
准备数据
准备数据的完整流程是:
-
读取文本文件并分成行,将行分成对
在词统计的类中:
英文分词选择nltk的word_tokenize
中文选择使用jieba分词(根据中文分词技术小结中总结,jieba效果并不是最好的,但是是最容易使用的)
-
标准化文本,按长度和内容过滤
- 英文统一转为Ascii
- 去掉中文中的多余空格
- 去掉中文中多余符号,例如连续的多个“-”、“!”等符号减少为1个
- 长度大于30的句子切分为两句而不是删掉
-
从成对的句子中制作单词列表
参考pytorch中seq2seq模型,构建词典代码如下:
以下是基本代码,我尝试了很多个版本代码,详情见具体代码,以下是尝试过的方法:
尝试深度学习进阶中提到的反转输入的方法加强seq2seq模型的性能并加速训练
尝试先将句子切分为token,然后组合为pair,而不是先根据maxlen截断再切分
尝试使用下面方法:
分词和词形还原:确保分词的准确性,并且在英文处理部分引入词形还原(Lemmatization),以处理单词的不同形式。
停用词去除:在英文和中文处理过程中去除常见的停用词,以减少噪声。
词汇对齐与扩充:在构建词典时,可以采用预训练的词向量(例如,Word2Vec、GloVe)进行词汇对齐与扩充,以提高词典的覆盖度和表示能力。
句子清理和标准化:进一步优化句子清理和标准化步骤,确保处理后的文本更加干净和一致。
数据增强:使用数据增强技术(如同义词替换、随机插入、删除等)来增加训练数据的多样性和丰富性。
长度大于30的句子切分为两句而不是直接删掉
将出现次数少于2次的低频率标记视为相同的未知(”
")标记
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
SOS_token = 0
EOS_token = 1
UNK_token = 2
MAX_LENGTH = 30
class Lang:
def __init__(self, name):
self.name = name
self.word2index = {"<UNK>": UNK_token}
self.word2count = {}
self.index2word = {0: "SOS", 1: "EOS", UNK_token: "<UNK>"}
self.n_words = 3 # Count SOS, EOS and UNK
def addSentence(self, sentence):
if self.name == "chin":
words = jieba.cut(sentence)
else:
words = sentence.split(' ')
for word in words:
# print(word)
self.addWord(word)
def addWord(self, word):
if word not in self.word2index:
self.word2index[word] = self.n_words
self.word2count[word] = 1
self.index2word[self.n_words] = word
self.n_words += 1
else:
self.word2count[word] += 1
然后分别对中文和英文构建词典:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 定义一个函数prepareData,用于准备训练数据。
def prepareData(filepath, reverse=False):
print("Preparing training data...")
# 调用readLangs函数读取语言数据,返回输入语言、输出语言和句子对。
input_lang, output_lang, pairs = readLangs(filepath, reverse)
print("Read %s sentence pairs" % len(pairs))
# 使用filterPairs函数过滤掉无效的句子对。
pairs = filterPairs(pairs)
print("Trimmed to %s sentence pairs" % len(pairs))
print("Counting words...")
# 遍历所有句子对,对输入语言和输出语言的每个句子进行单词计数。
for pair in pairs:
input_lang.addSentence(pair[0])
output_lang.addSentence(pair[1])
print("Counted words:")
print(input_lang.name, input_lang.n_words)
print(output_lang.name, output_lang.n_words)
return input_lang, output_lang, pairs
结果如下(展示前10个词典中词汇):
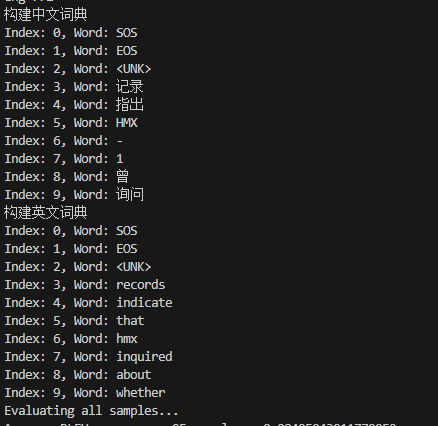
模型搭建
整个模型分为3个代码块:Encoder、Attention、Decoder。
-
Encoder层负责处理输入数据,并输出$ s_0$和$ [h_1,…,h_m]$;
-
Attention层负责根据Encoder层的输出,生成$a_1,…,a_m$和$ c_i$;
-
Decoder层负责处理Attention层的输出,解码得到$s_i$;
seq2seq + attention总体概览
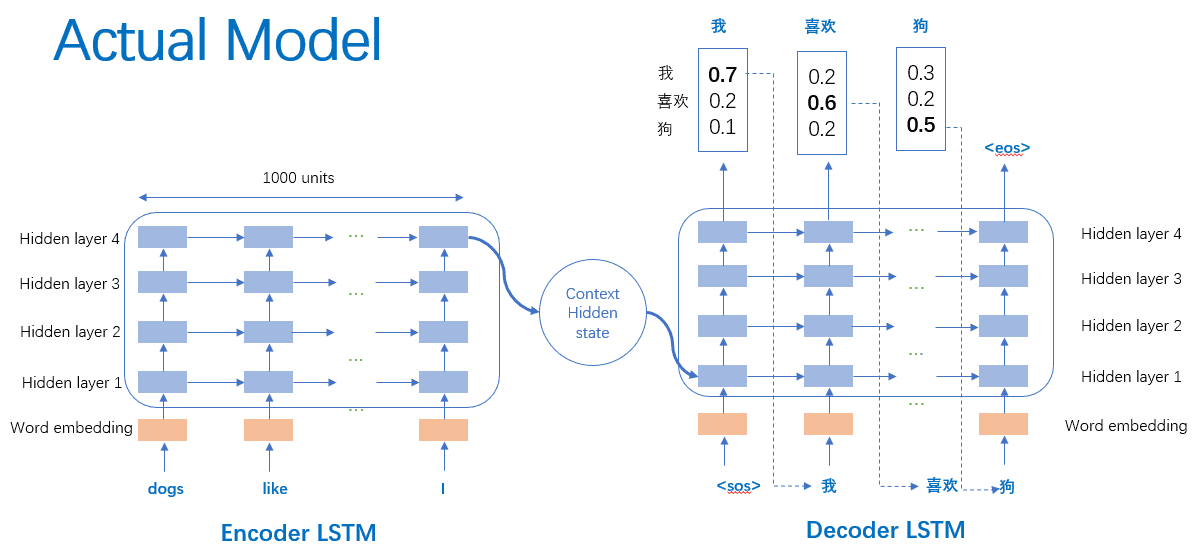
encoder
Encoder是一种将输入序列转换为一个包含其重要信息的固定大小向量的机制。在自然语言处理中,句子是由多个单词组成的序列。例如,句子 “I love programming” 包含三个单词。为了使计算机能够处理这个句子,我们需要将每个单词转换为一个向量,这个向量包含了单词的语义信息。然后,我们将这些向量传递给一个神经网络,使其能够理解整个句子。
Encoder的主要任务是将输入的序列数据转换为一个包含其重要信息的固定大小向量。它通过嵌入层将单词转换为向量,然后通过GRU处理这些向量,得到序列的输出和最终的隐藏状态。这些输出和隐藏状态将被传递给解码器(Decoder),用于生成目标序列。
可以通过以下代码来实现一个Encoder:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class EncoderRNN(nn.Module):
def __init__(self, input_size, hidden_size, num_layers=2, dropout_p=0.1):
super(EncoderRNN, self).__init__()
# 定义隐藏层的大小。
self.hidden_size = hidden_size
# 定义循环神经网络的层数。
self.num_layers = num_layers
# 创建一个嵌入层,用于将输入序列中的单词转换为固定大小的向量。
# input_size是词汇表的大小,hidden_size是嵌入向量的维度。
self.embedding = nn.Embedding(input_size, hidden_size)
# 创建一个门控循环单元(GRU)层,用于处理序列数据。
# hidden_size是GRU层的隐藏层大小,num_layers是堆叠的层数。
# batch_first=True表示输入和输出的张量中第一个维度是批次大小。
# dropout=dropout_p用于在不同层之间添加dropout以防止过拟合,如果num_layers只有1层,则不添加dropout。
self.gru = nn.GRU(hidden_size, hidden_size, num_layers=num_layers, batch_first=True, dropout=dropout_p if num_layers > 1 else 0)
# forward方法定义了数据通过网络的前向传播过程。
def forward(self, input):
# 将输入序列通过嵌入层,得到嵌入后的序列向量。
embedded = self.embedding(input)
# 将嵌入后的序列通过GRU层进行处理,得到输出和最终的隐藏状态。
# output是序列在每个时间步的输出,hidden是序列处理完后的最终隐藏状态。
output, hidden = self.gru(embedded)
# 返回序列的输出和最终的隐藏状态。
return output, hidden
- 嵌入层(Embedding Layer)
嵌入层的作用是将输入序列中的单词转换为固定大小的向量。可以将其想象为一个查找表,每个单词都有一个对应的向量表示。
1
self.embedding = nn.Embedding(input_size, hidden_size)
这里,input_size 是词汇表的大小,也就是我们模型所能识别的单词数量。hidden_size 是每个单词向量的维度。例如,如果 input_size 为10000,hidden_size 为256,那么嵌入层将每个单词转换为一个256维的向量。
- 循环神经网络(GRU)
GRU(门控循环单元)是一种处理序列数据的神经网络。它能够记住序列中的信息,并且在长序列中效果很好。我们用GRU来处理嵌入后的单词向量。
对比LSTM后发现10k数据集上GRU的效果更好,100k的数据集上LSTM的效果更好。
1
self.gru = nn.GRU(hidden_size, hidden_size, num_layers=num_layers, batch_first=True, dropout=dropout_p if num_layers > 1 else 0)
这里,hidden_size 决定了GRU每一层的隐藏状态的大小。num_layers 是GRU的层数,batch_first=True 表示输入和输出的张量的第一个维度是批次大小。dropout_p 是一个防止过拟合的技术,在训练时会随机忽略一些GRU单元的输出。
- 前向传播(Forward Pass)
前向传播是指数据通过神经网络进行处理的过程。在这个过程中,我们将输入序列通过嵌入层,得到嵌入后的序列向量。然后,将嵌入后的序列向量传递给GRU进行处理,得到输出和最终的隐藏状态。
1
2
3
4
def forward(self, input):
embedded = self.embedding(input)
output, hidden = self.gru(embedded)
return output, hidden
attention
计算注意力权重是通过另一个前馈层 attn 完成的,使用解码器的输入和隐藏状态作为输入。因为训练数据中有各种大小的句子,所以要实际创建和训练该层,我们必须选择它可以应用的最大句子长度(输入长度,用于编码器输出)。最大长度的句子将使用所有注意力权重,而较短的句子将仅使用前几个。
Bahdanau 注意,又称加法注意,是序列到序列模型中常用的一种注意机制,尤其是在神经机器翻译任务中。这种注意力机制采用学习的对齐模型来计算编码器和解码器隐藏状态之间的注意力分数。它利用前馈神经网络来计算对齐分数。
相似度计算:
\[\mathrm{a(s_{i-1},h_j)=V_a^T\tanh(W_as_{i-1}+U_ah_j)}\\\]之前介绍attention中介绍到的:一个输入位置j的hidden vector与当前输出位置的关联性$similarity(s_{t-1},h_j)$,这个有很多种计算方式,其实就是相似度的计算方式(也叫对齐函数),Bahdanau 注意用上面这个函数作为对齐函数
注意力分数(注意力权重):
\[\mathrm{\alpha_i=softmax(a(s_{i-1},h_1),a(s_{i-1},h_2),...a(s_{i-1},h_l))}\]不难发现计算完$W_as_{i-1} + U_ah_j$ ,其维度固定成$[hiddenSize ,1]$,所以我们也称其为对齐,具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 使用additive attention
class BahdanauAttention(nn.Module):
def __init__(self, hidden_size):
super(BahdanauAttention, self).__init__()
# 定义一个线性层Wa,将输入的隐藏状态映射到hidden_size维度的空间
self.Wa = nn.Linear(hidden_size, hidden_size)
# 定义一个线性层Ua,将输入的键(keys)映射到hidden_size维度的空间
self.Ua = nn.Linear(hidden_size, hidden_size)
# 定义一个线性层Va,将上一步的和映射到1维空间,用于计算注意力分数
self.Va = nn.Linear(hidden_size, 1)
# 前向传播函数,计算注意力机制的输出
def forward(self, query, keys):
# 使用线性层Wa处理查询(query),然后使用tanh激活函数
# 将处理后的查询与线性层Ua处理的键(keys)相加
# 然后使用线性层Va将结果映射到1维,得到注意力分数的初步计算结果
scores = self.Va(torch.tanh(self.Wa(query) + self.Ua(keys)))
# 将分数的维度调整为适合softmax操作的形状,即(batch_size, seq_len, 1)
scores = scores.squeeze(2).unsqueeze(1)
# 应用softmax函数计算权重,这些权重表示每个键在生成当前输出时的重要性
weights = F.softmax(scores, dim=-1)
# 使用计算出的权重和键(keys)进行矩阵乘法,得到加权的上下文信息
context = torch.bmm(weights, keys)
# 返回加权的上下文信息和对应的权重
return context, weights
- 这里初始化了三个线性层,其实也就是上面公式中的$W_a$、$U_a$和$V_a$矩阵,是待学习的参数:
1
2
3
self.Wa = nn.Linear(hidden_size, hidden_size)
self.Ua = nn.Linear(hidden_size, hidden_size)
self.Va = nn.Linear(hidden_size, 1)
- 计算相似度
1
scores = self.Va(torch.tanh(self.Wa(query) + self.Ua(keys)))
这里首先使用Wa和Ua分别处理query和keys,然后将它们的输出相加。接着,将这个和通过tanh激活函数,最后通过Va生成注意力分数。数学上,如果我们将query表示为( q ),将keys表示为( k ),那么注意力分数的计算可以表示为:
这里的q是decoder的上一次输出$s_{i-1}$,k是隐藏层$h_j$。
- 计算注意力分数
1
weights = F.softmax(scores, dim=-1)
之后用使用softmax函数对调整后的分数应用,计算每个位置的权重。这将确保所有权重的和为1,表示对keys的归一化注意力分布。这里的dim=-1表示沿着最后一个维度(即新增加的维度)应用softmax。
- 计算加权上下文信息:
1
context = torch.bmm(weights, keys)
这一步通过矩阵乘法计算加权的上下文信息。weights是归一化的注意力权重,keys是decoder的输出。这里使用的是二维矩阵乘法bmm,它将weights的最后一个维度和keys的第一个维度进行广播和乘法操作。数学上,如果我们将权重矩阵表示为( w ),那么加权上下文的计算可以表示为:
其中,( w )的每一行是对应于keys中每个元素的注意力权重。
函数返回两个值:加权的上下文信息context和对应的注意力权重weights。上下文信息可以用于后续的解码步骤,而注意力权重可以用于分析模型的注意力分布。
decoder
Decoder的任务是将Encoder生成的固定大小向量转换回原始的序列数据。在序列到序列的模型中,比如翻译或者对话生成中,Decoder使用来自Encoder的输出向量以及前一步生成的单词来预测下一个单词。如下图,decoder要将attention层的上下文向量context于上一次的输出s拼接到一起作为RNN网络的输入。
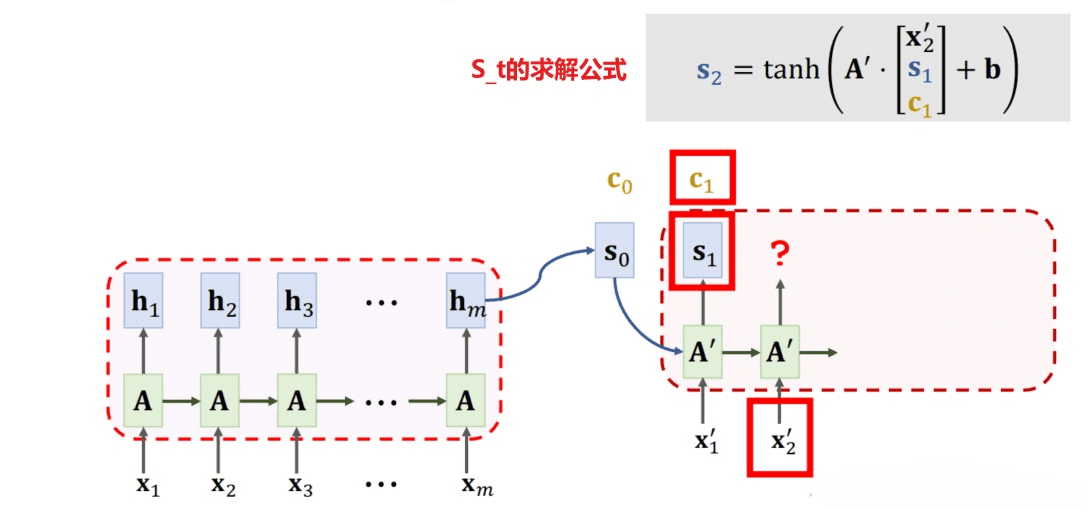
Decoder就是一个解码器,它根据编码器提供的信息一步一步地生成输出。假设我们已经用Encoder将一个英文句子转换成了一个固定大小的向量作为中间表示,现在我们要用Decoder将这个向量转换回一个中文句子。
Decoder的主要任务是将Encoder生成的固定大小向量转换回原始的序列数据。它通过嵌入层将输入的单词转换为向量,通过GRU处理这些向量,然后通过线性层和Softmax层生成下一个单词的概率分布。通过结合Attention机制,Decoder可以在生成每个单词时动态地关注Encoder输出的不同部分,从而生成更加准确和流畅的序列。为了使Decoder更加高效,可以使用Attention机制。Attention机制可以让Decoder在生成每个单词时关注Encoder输出的不同部分,从而生成更加准确的结果。
下面是基于attention机制的Decoder的实现代码(之后还会在此基础上实现beam search):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class AttnDecoderRNN(nn.Module):
def __init__(self, hidden_size, output_size, num_layers=2, dropout_p=0.1):
super(AttnDecoderRNN, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.embedding = nn.Embedding(output_size, hidden_size)
# self.attention = BahdanauAttention(hidden_size)
self.attention = LuongAttention(hidden_size)
self.gru = nn.GRU(2 * hidden_size, hidden_size, num_layers=num_layers, batch_first=True, dropout=dropout_p if num_layers > 1 else 0)
#经过全连接层输出,映射成单词的概率分布形式
self.out = nn.Linear(hidden_size, output_size)
self.dropout = nn.Dropout(dropout_p)
def forward(self, encoder_outputs, encoder_hidden, target_tensor=None):
batch_size = encoder_outputs.size(0)
decoder_input = torch.empty(batch_size, 1, dtype=torch.long, device=device).fill_(SOS_token)
decoder_hidden = encoder_hidden
decoder_outputs = []
attentions = []
for i in range(MAX_LENGTH):
decoder_output, decoder_hidden, attn_weights = self.forward_step(
decoder_input, decoder_hidden, encoder_outputs
)
decoder_outputs.append(decoder_output)
attentions.append(attn_weights)
if target_tensor is not None:
decoder_input = target_tensor[:, i].unsqueeze(1) # Teacher forcing
#推理时默认用贪心搜索greedy search
else:
_, topi = decoder_output.topk(1)
decoder_input = topi.squeeze(-1).detach() # detach from history as input
decoder_outputs = torch.cat(decoder_outputs, dim=1)
decoder_outputs = F.log_softmax(decoder_outputs, dim=-1)
attentions = torch.cat(attentions, dim=1)
return decoder_outputs, decoder_hidden, attentions
def forward_step(self, input, hidden, encoder_outputs):
embedded = self.dropout(self.embedding(input))
query = hidden[-1].unsqueeze(1) # Use the last layer's hidden state for attention
context, attn_weights = self.attention(query, encoder_outputs)
input_gru = torch.cat((embedded, context), dim=2)
output, hidden = self.gru(input_gru, hidden)
output = self.out(output)
return output, hidden, attn_weights
- 嵌入层(Embedding Layer)
嵌入层的作用是将Decoder的输入(通常是前一步生成的单词)转换为向量。
1
self.embedding = nn.Embedding(output_size, hidden_size)
output_size 是词汇表的大小,也就是我们模型所能生成的单词数量。hidden_size 是每个单词向量的维度。例如,如果 output_size 为10000,hidden_size 为256,那么嵌入层将每个单词转换为一个256维的向量。
- 循环神经网络(GRU)
GRU在Decoder中用来处理嵌入后的单词向量,并生成新的隐藏状态和输出。
1
self.gru = nn.GRU(hidden_size, hidden_size, num_layers=num_layers, batch_first=True, dropout=dropout_p if num_layers > 1 else 0)
这里,hidden_size 决定了GRU每一层的隐藏状态的大小。num_layers 是GRU的层数,batch_first=True 表示输入和输出的张量的第一个维度是批次大小。dropout_p 是一个防止过拟合的技术,在训练时会随机忽略一些GRU单元的输出。
- 线性层和Softmax层
线性层将GRU的输出转换为词汇表大小的向量,Softmax层将这个向量转换为概率分布,用于预测下一个单词。
1
2
self.out = nn.Linear(hidden_size, output_size)
self.softmax = nn.LogSoftmax(dim=1)
- Attention层
Attention层会计算Decoder当前时间步的隐藏状态与Encoder输出的每个时间步的隐藏状态之间的相关性,从而决定Decoder应该关注Encoder输出的哪些部分。
1
2
3
self.attn = BahdanauAttention(hidden_size)
或者
self.attention = LuongAttention(hidden_size)
- 前向传播
在前向传播过程中,我们首先将Decoder的输入通过嵌入层和GRU处理,然后通过Attention层计算上下文向量,最后将GRU的输出和上下文向量拼接起来,通过线性层和Softmax层生成下一个单词的概率分布。多次重复以上步骤,直到输出为EOS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 执行解码器的单个前向传播步骤
def forward_step(self, input, hidden, encoder_outputs):
# 将输入通过嵌入层,并通过dropout层
embedded = self.dropout(self.embedding(input))
# 使用上一步的隐藏状态作为查询,计算注意力权重和上下文向量
query = hidden[-1].unsqueeze(1) # Use the last layer's hidden state for attention
context, attn_weights = self.attention(query, encoder_outputs)
# 将嵌入的输入和上下文向量在最后一个维度上进行拼接
input_gru = torch.cat((embedded, context), dim=2)
# 将拼接后的输入传递给GRU层,并获取输出和新的隐藏状态
output, hidden = self.gru(input_gru, hidden)
# 将GRU的输出通过全连接层
output = self.out(output)
# 返回当前步骤的输出、隐藏状态和注意力权重
return output, hidden, attn_weights
不同的对齐函数
在注意力机制中,对齐函数(alignment function)是用来计算当前解码器隐藏状态和编码器隐藏状态之间的相关性。不同的对齐函数可以有不同的计算方式,并会对最终模型的性能产生影响。在这里,我们比较Bahdanau注意力(也称为加法注意力)和Luong注意力(也称为乘法注意力)的区别,并分析为什么在本次实验中,Luong注意力效果更好。
Bahdanau注意力(加法注意力)
Bahdanau注意力的对齐函数通过一个前馈神经网络计算解码器隐藏状态和编码器隐藏状态之间的相关性。其计算公式如下:
\[a(s_{i-1}, h_j) = V_a^T \tanh(W_a s_{i-1} + U_a h_j)\]其中,$V_a$、$W_a$ 和 $U_a$ 都是可学习的参数矩阵。这个方法的优点是能够更灵活地捕捉解码器和编码器隐藏状态之间的复杂关系。
Luong注意力(乘法注意力)
Luong注意力的对齐函数有三种变体:dot、general 和 concat。它们的共同点是都通过乘法计算相关性,其中 dot 和 general 是乘法计算,而 concat 是先拼接再通过前馈神经网络计算。其计算公式如下:
\[\mathrm{score}(h_t, \bar{h}_s) = \begin{cases} h_t^\top \bar{h}_s & \text{dot} \\ h_t^\top W_a \bar{h}_s & \text{general} \\ v_a^\top \tanh\left(W_a [h_t; \bar{h}_s] \right) & \text{concat} \end{cases}\]在本次实验中,我们使用了general变体,其具体实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class LuongAttention(nn.Module):
def __init__(self, hidden_size):
super(LuongAttention, self).__init__()
# 初始化一个线性层Wa,用于将键(keys)的维度从hidden_size映射到hidden_size
self.Wa = nn.Linear(hidden_size, hidden_size)
def forward(self, query, keys):
# 将查询query与键keys通过线性层Wa进行变换
keys_transformed = self.Wa(keys)
# 计算查询query与变换后的键keys_transformed的点积,得到注意力分数
# 使用矩阵乘法torch.bmm,query的维度为[batch_size, 1, hidden_size]
# keys_transformed.transpose(1, 2)的维度为[batch_size, hidden_size, seq_len]
# 点积结果scores的维度为[batch_size, 1, seq_len]
scores = torch.bmm(query, keys_transformed.transpose(1, 2))
# 对得到的分数应用softmax函数,得到归一化的注意力权重
# softmax沿着最后一个维度进行计算,确保每个位置的权重和为1
weights = F.softmax(scores, dim=-1)
# 使用得到的注意力权重weights和原始的键keys进行矩阵乘法
# 计算加权求和,得到上下文向量context
# weights的维度为[batch_size, 1, seq_len],keys的维度为[batch_size, seq_len, hidden_size]
# 上下文向量context的维度为[batch_size, 1, hidden_size]
context = torch.bmm(weights, keys)
return context, weights
理论分析:
-
计算效率:Bahdanau注意力需要对每个解码时间步和编码时间步计算一次前馈神经网络的输出,这在计算上是昂贵的。尤其是在长序列情况下,计算复杂度较高。而Luong注意力的dot和general变体仅仅是矩阵乘法,计算复杂度较低,更加高效。
-
性能:在实际应用中,尤其是像本次实验的机器翻译这样的任务中,Luong注意力的表现通常优于Bahdanau注意力。这是因为乘法注意力(dot和general)能够更直接地捕捉到解码器和编码器隐藏状态之间的相似性,而不用通过复杂的前馈神经网络。
-
对齐效果:Luong注意力的general变体通过一个线性变换($W_a$)调整了编码器隐藏状态的表示,使其更好地与解码器隐藏状态匹配。这种直接的相似性计算在很多情况下能够提供更精确的对齐效果。
在本次实验中,使用Luong注意力相比Bahdanau注意力效果确实好了很多。并且Luong注意力的参数较少,相比Bahdanau注意力更容易训练和优化。在本次实验中,这可能使得模型更快地达到最佳状态。
Teacher Forcing 和 Free Running
在循环神经网络(RNN)的训练初期,模型的预测能力通常较弱,难以生成高质量的输出。在这一阶段,如果某个单元产生了低质量的预测结果,这种不良效应可能会沿着时间序列传播,对后续单元的学习造成负面影响。
为了解决这一问题,引入了一种称为”教师强制”(Teacher Forcing)的训练策略。该方法在深度学习领域,特别是在开发用于机器翻译、文本摘要、图像字幕等任务的语言模型中发挥着至关重要的作用。在教师强制策略下,模型在每个时间步并不是简单地使用前一状态的输出作为当前状态的输入,而是采用训练数据集中的ground truth(即真实值)作为下一个状态的输入。这种策略通过直接提供正确的信息,有助于加速模型的收敛过程,并提高其学习效率。通过这种方式,模型能够在训练过程中更快地学习到数据的内在规律,从而在实际应用中生成更加准确和可靠的结果。
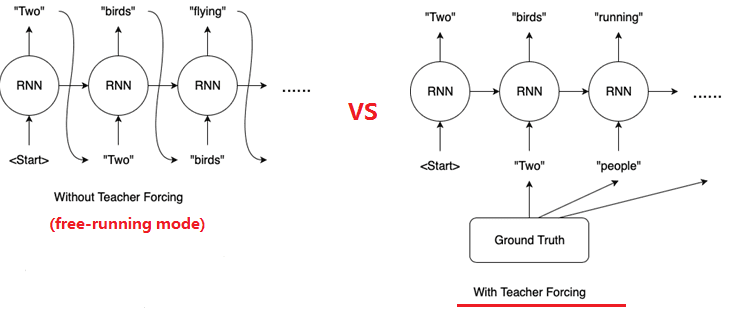
核心代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
def forward(self, encoder_outputs, encoder_hidden, target_tensor=None):
...
for i in range(MAX_LENGTH):
...
if target_tensor is not None:
decoder_input = target_tensor[:, i].unsqueeze(1) # Teacher forcing
#推理时默认用贪心搜索greedy search
else:
_, topi = decoder_output.topk(1)
decoder_input = topi.squeeze(-1).detach() # detach from history as input
...
return decoder_outputs, decoder_hidden, attentions
教师强制(Teacher Forcing)虽然在训练阶段能够显著提高模型的效率和性能,但它也存在一些固有的局限性。正如俗话所说,“依赖老师带领的孩子难以独立远行”,这一比喻同样适用于教师强制策略。在这种策略下,模型在训练过程中过度依赖于标签数据,即标准答案(ground truth),这可能导致模型在面对未知或与训练数据分布不一致的测试数据时,表现出脆弱性。
具体来说,模型在训练时由于总是获得正确的前一个状态作为输入,可能会形成对这种理想化情况的依赖。然而,在实际应用或测试阶段,模型无法获得这种ground truth的支持,而必须依赖自身生成的序列进行迭代预测。如果当前生成的序列与训练数据存在显著差异,模型的预测能力可能会急剧下降,导致性能的不稳定。
此外,教师强制策略可能会限制模型的跨领域(cross-domain)泛化能力。当测试数据集与训练数据集分属不同的领域时,模型由于缺乏对多样化数据分布的适应性,其性能可能会受到较大影响。这是因为模型在训练过程中未能充分学习到如何从自身预测的错误中恢复并继续生成合理的序列。
为了保持Teacher Forcing的优势并克服困难,我在训练前期保持使用Teacher Forcing,后期则Teacher Forcing和Free Running一起使用,加速训练的同时保证其泛化能力。
不同的Teacher Forcing比率(teacher_forcing_ratio)会对模型的收敛速度和最终性能产生显著影响。下面详细分析在teacher_forcing_ratio分别设置为0、0.5和1时,对模型收敛速度的影响。
Teacher Forcing Ratio为0
当teacher_forcing_ratio设置为0时,模型在训练过程中完全依赖自身生成的序列作为下一步的输入。这种情况下,模型的收敛速度较慢,但有助于提高模型的鲁棒性,因为模型在训练过程中面临更多的不确定性和挑战。
训练表现:
- 在第60个epoch时,loss下降到1以下。
- 训练200个epoch后,最低的loss为0.1930。
1
2
3
4
5
6
7
8
9
epoch:55 5m 2s (- 13m 18s) (27%) loss:1.0172
save the best model successful!
epoch:60 5m 30s (- 12m 50s) (30%) loss:0.9323
save the best model successful!
...
epoch:190 17m 35s (- 0m 55s) (95%) loss:0.1930
save the best model successful!
epoch:195 18m 3s (- 0m 27s) (97%) loss:0.1931
epoch:200 18m 30s (- 0m 0s) (100%) loss:0.1989
Teacher Forcing Ratio为0.5
当teacher_forcing_ratio设置为0.5时,模型在一半的情况下使用真实目标序列,另一半情况下使用自身生成的序列作为输入。这种平衡的策略既能加速模型收敛,又能提高模型的鲁棒性。
训练表现:
- 在第55个epoch时,loss下降到1以下。
- 训练200个epoch后,最低的loss为0.1675。
1
2
3
4
5
6
7
8
9
10
epoch:50 4m 51s (- 14m 34s) (25%) loss:1.0618
save the best model successful!
epoch:55 5m 18s (- 14m 0s) (27%) loss:0.9681
save the best model successful!
...
epoch:180 16m 19s (- 1m 48s) (90%) loss:0.1562
epoch:185 16m 45s (- 1m 21s) (92%) loss:0.1618
epoch:190 17m 12s (- 0m 54s) (95%) loss:0.1617
epoch:195 17m 38s (- 0m 27s) (97%) loss:0.1625
epoch:200 18m 4s (- 0m 0s) (100%) loss:0.1675
Teacher Forcing Ratio为1
当teacher_forcing_ratio设置为1时,模型在训练过程中始终使用真实的目标序列作为输入。这种策略可以显著加速模型的收敛,但可能导致模型对真实序列的依赖过强,在测试时性能可能不如训练时表现好。
训练表现:
- 在第30个epoch时,loss下降到1以下。
- 训练200个epoch后,最低的loss为0.0465。
1
2
3
4
5
6
7
8
9
10
epoch:25 2m 5s (- 14m 37s) (12%) loss:1.0931
save the best model successful!
epoch:30 2m 31s (- 14m 16s) (15%) loss:0.8800
save the best model successful!
...
epoch:180 15m 8s (- 1m 40s) (90%) loss:0.0465
epoch:185 15m 34s (- 1m 15s) (92%) loss:0.0466
epoch:190 15m 59s (- 0m 50s) (95%) loss:0.0502
epoch:195 16m 24s (- 0m 25s) (97%) loss:0.0492
epoch:200 16m 49s (- 0m 0s) (100%) loss:0.0494
总结
通过对比不同teacher_forcing_ratio下的训练表现,可以得出以下结论:
- Teacher Forcing Ratio为0:模型完全依赖自身生成的序列,收敛速度最慢,但最终的鲁棒性较高,避免了过度依赖真实序列。
- Teacher Forcing Ratio为0.5:模型在使用真实序列和自身生成序列之间找到平衡,既能较快收敛,又能保持一定的鲁棒性。
- Teacher Forcing Ratio为1:模型完全依赖真实序列,收敛速度最快,但可能导致对真实序列的依赖过强,在实际应用中表现可能不稳定。
在实际应用中,选择合适的teacher_forcing_ratio需要综合考虑模型的收敛速度和最终性能。通常情况下,0.5是一个较为理想的选择,能够在收敛速度和模型鲁棒性之间取得平衡。
greedy 和 beam-search 解码策略
在机器翻译或序列生成任务中,解码策略是决定如何从解码器中生成序列的关键步骤。以下是两种常见的解码策略:贪婪解码(Greedy Decoding)和束搜索解码(Beam Search Decoding)。
贪婪解码(Greedy Decoding)
贪婪解码是一种简单直观的解码策略,它在每一步都选择概率最高的词作为输出。具体来说:
- 初始化:使用一个特殊的起始符号(如
<SOS>)作为序列的开始。 - 迭代解码:在每一步,解码器生成一个词的概率分布。
- 选择最高概率词:从这个分布中选择概率最高的词作为当前步骤的输出。
- 终止条件:当生成序列达到最大长度或生成了结束符号(如
<EOS>)时,解码结束。
贪婪解码的优点是实现简单,计算效率高。但它的主要缺点是可能会错过更好的序列,因为它只考虑当前步骤的最高概率词,而不考虑这个词对后续步骤的影响。
贪心的实现也就是每次选最好的那个
1
2
3
4
5
6
7
8
9
10
11
def forward(self, encoder_outputs, encoder_hidden, target_tensor=None):
...
for i in range(MAX_LENGTH):
...
#推理时默认用贪心搜索greedy search
else:
_, topi = decoder_output.topk(1)
decoder_input = topi.squeeze(-1).detach() # detach from history as input
...
return decoder_outputs, decoder_hidden, attentions
束搜索解码(Beam Search Decoding)
束搜索解码是一种更复杂的解码策略,它在每一步都考虑多个候选词,以提高生成序列的整体质量。具体步骤如下:
- 初始化:与贪婪解码相同,使用起始符号开始序列。
- 维护多个候选:在每一步,解码器生成所有可能的词的概率分布,然后选择概率最高的
k个词作为候选(这里的k被称为束宽,即同时考虑的候选序列的数量)。 - 扩展序列:将每个候选词添加到当前序列的末尾,形成新的候选序列。
- 重新排序:根据新生成的候选序列的概率重新排序,选择概率最高的
k个序列作为下一步的候选。 - 终止条件:当所有候选序列都生成了结束符号或达到最大长度时,选择概率最高的序列作为最终输出。
束搜索解码的优点是可以找到更优的序列,因为它考虑了当前步骤的多个候选词对后续步骤的影响。然而,它的缺点是计算成本较高,因为需要同时维护多个候选序列。
实现代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
def beam_search_decode(self, encoder_outputs, encoder_hidden, beam_width=3, max_length=MAX_LENGTH):
# 获取编码器输出的批量大小
batch_size = encoder_outputs.size(0)
# 初始化解码器输入为序列的起始标记SOS_token
decoder_input = torch.empty(batch_size, 1, dtype=torch.long, device=device).fill_(SOS_token)
# 将编码器的隐藏状态作为解码器的初始隐藏状态
decoder_hidden = encoder_hidden
# 使用优先队列管理束搜索,每个元素是一个元组,包含(对数概率,序列,隐藏状态,注意力权重)
beams = [(0, [SOS_token], decoder_hidden, [])]
# 循环直到达到最大长度或所有序列都结束
for _ in range(max_length):
new_beams = []
# 遍历当前所有束
for log_prob, seq, hidden, attn_weights in beams:
# 如果序列以结束标记EOS_token结束,则将其添加到新的束中,不进行扩展
if seq[-1] == EOS_token:
new_beams.append((log_prob, seq, hidden, attn_weights))
continue
# 将上一个预测的单词作为当前步的输入
decoder_input = torch.tensor([seq[-1]], device=device).view(1, 1)
# 执行解码器的单个步骤前向传播,获取当前步的输出、隐藏状态和注意力权重
decoder_output, hidden, attn_weight = self.forward_step(decoder_input, hidden, encoder_outputs)
# 从解码器输出中获取概率最高的k个候选单词
topk_log_probs, topk_indices = decoder_output.topk(beam_width)
# 遍历概率最高的k个候选单词
for k in range(beam_width):
new_token = topk_indices[0][0][k].item()
# 跳过起始标记SOS_token,因为它不应该被重复添加到序列中
if new_token == SOS_token:
continue
# 计算新的对数概率,即当前对数概率加上新单词的对数概率
new_log_prob = log_prob + topk_log_probs[0][0][k].item()
# 构建新的序列,包含新预测的单词
new_seq = seq + [new_token]
# 将新步的注意力权重添加到序列的注意力权重列表中
new_attn_weights = attn_weights + [attn_weight]
# 将新构建的束添加到新的候选束列表中
new_beams.append((new_log_prob, new_seq, hidden, new_attn_weights))
# 从所有新的候选束中选择概率最高的beam_width个束
beams = heapq.nlargest(beam_width, new_beams, key=lambda x: x[0])
# 选择概率最高的序列作为最佳序列
best_seq = beams[0][1]
# 如果存在注意力权重,将它们在序列长度维度上进行拼接
attentions = torch.cat([attns for attns in beams[0][3]], dim=1) if beams[0][3] else None
发现在简单的模型中使用束搜索解码可以大幅提升准确率,但是同时也发现一个问题,就是推理所需时间大大增加。
BLEU模型评估
BLEU(Bilingual Evaluation Understudy),即双语评估替补。所谓替补就是代替人类来评估机器翻译的每一个输出结果。Bleu score 所做的,给定一个机器生成的翻译,自动计算一个分数,衡量机器翻译的好坏。取值范围是[0, 1],越接近1,表明翻译质量越好。
计算公式如下:
\[BLEU=BP*exp(\frac1n\sum_{i=1}^NP_n)\]其中,BP是简短惩罚因子,惩罚一句话的长度过短,防止训练结果倾向短句的现象,其表达式为:
\[BP=\begin{cases}1,&\mathrm{if~}MT\text{output length}>\text{reference output length}\\exp(1-MToutputlength/referenceoutputlength),&\mathrm{otherwise}&\end{cases}\]Pn,是基于n-gram的精确度,其表达公式为:
\[P_n=\frac{\sum_{n-gram\in y\text{ CounterClip(n-gram)}}}{\sum_{n-gram\in y\text{ Counter(n-gram)}}}\]实现时可以调用nltk的sentence_bleu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from nltk.translate.bleu_score import sentence_bleu
def evaluateAll(encoder, decoder, input_lang, output_lang, pairs, method="default",n=10, beam_width=3):
print('Evaluating all samples...')
total_bleu_score = 0.0
for pair in pairs:
if method == 'beam_search':
output_words, _ = evaluateBeamSearch(encoder, decoder, pair[0], input_lang, output_lang, beam_width)
else:
output_words, _ = evaluate(encoder, decoder, pair[0], input_lang, output_lang)
output_sentence = ' '.join(output_words)
# Calculate BLEU score
reference = [pair[1].split()]
candidate = output_sentence.split()
bleu_score = sentence_bleu(reference, candidate)
total_bleu_score += bleu_score
avg_bleu_score = total_bleu_score / len(pairs)
print('Average BLEU score over {} samples = {}'.format(len(pairs), avg_bleu_score))
attention可视化
在此部分,我们通过对Attention权重矩阵的可视化展示,可以更好地理解模型在翻译任务中的工作机制。通过随机抽取BLEU分数较高的结果,我们能够观察Attention权重矩阵的变化,并了解哪部分翻译对应哪部分源文字。以下是代码示例以及具体的可视化分析。
可视化代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import matplotlib.pyplot as plt
import jieba
from matplotlib import ticker
def showAttention(input_sentence, output_words, attentions):
# 设置图形和颜色条
fig = plt.figure()
ax = fig.add_subplot(111) # 创建一个子图,111表示1行1列的第一个
# 转置注意力矩阵以旋转90度,以便行列与输入输出序列对齐
# 使用'bone'颜色映射,浅色表示高注意力权重,深色表示低注意力权重
cax = ax.matshow(attentions.cpu().numpy().transpose(), cmap='bone')
fig.colorbar(cax) # 为图形添加颜色条
# 使用结巴分词对输入句子进行分词,并在末尾添加结束标记'<EOS>'
input_tokens = list(jieba.cut(input_sentence)) + ['<EOS>']
output_tokens = output_words # 输出序列的单词列表
# 设置x轴和y轴的刻度位置和标签
# 将输出序列的单词设置为x轴标签,并将输入序列的分词结果设置为y轴标签
ax.set_xticks(range(len(output_tokens)))
ax.set_xticklabels(output_tokens, rotation=90) # 将x轴标签旋转90度,便于阅读
ax.set_yticks(range(len(input_tokens)))
ax.set_yticklabels(input_tokens) # y轴标签为输入序列的分词结果
# 确保每个刻度处都有标签显示
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
# 显示图形
plt.show()
以下展示了随机抽取的几组BLEU分数较高的翻译结果的Attention权重矩阵的可视化图,并对每个图进行了详细分析。
可视化结果1
1
2
3
4
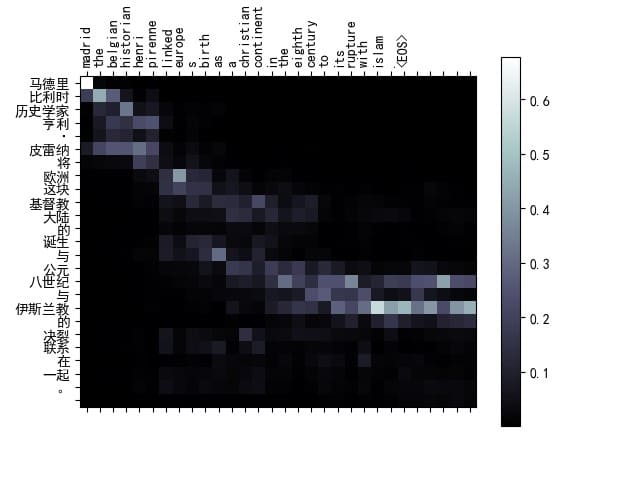
input= 马德里比利时历史学家亨利·皮雷纳将欧洲这块基督教大陆的诞生与公元八世纪与伊斯兰教的决裂联系在一起。
target= madrid the belgian historian henri pirenne linked europe s birth as a christian continent in the eighth century to its rupture with islam .
output= madrid the belgian historian henri pirenne linked europe s birth as a christian continent in the eighth century to its rupture with islam . <EOS>
BLEU score = 1
从Attention矩阵图中可以看出,模型在翻译过程中对于输入句子的关键部分给予了较高的注意力权重。例如,对于“欧洲这块基督教大陆的诞生”部分,模型能够准确地将其对应到输出中的“Europe’s birth”、“christian”和“continent”。这种精确的对齐关系说明模型在处理长句子和复杂结构时具有较高的翻译准确度。
可视化结果2
1
2
3
4
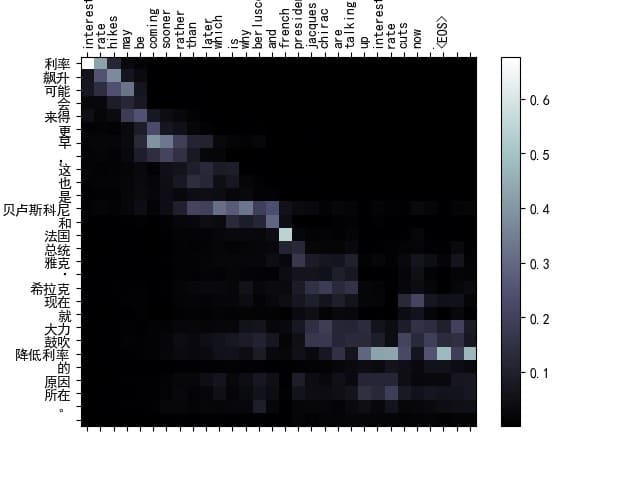
input= 利率飙升可能会来得更早,这也是贝卢斯科尼和法国总统雅克·希拉克现在就大力鼓吹降低利率的原因所在。
target= interest rate hikes may be coming sooner rather than later which is why berlusconi and french president jacques chirac are talking up interest rate cuts now .
output= interest rate hikes may be coming sooner rather than later which is why berlusconi and french president jacques chirac are talking up interest rate cuts now . <EOS>
BLEU score = 1
从Attention矩阵图中可以看出,模型能够准确地将输入句子的核心内容与输出对齐,尤其是在涉及人名和特定术语时。比如,“雅克·希拉克”和“Jacques Chirac”在模型的注意力矩阵中被正确地对齐,说明模型在处理人名和术语翻译时表现良好。
可视化结果3
1
2
3
4
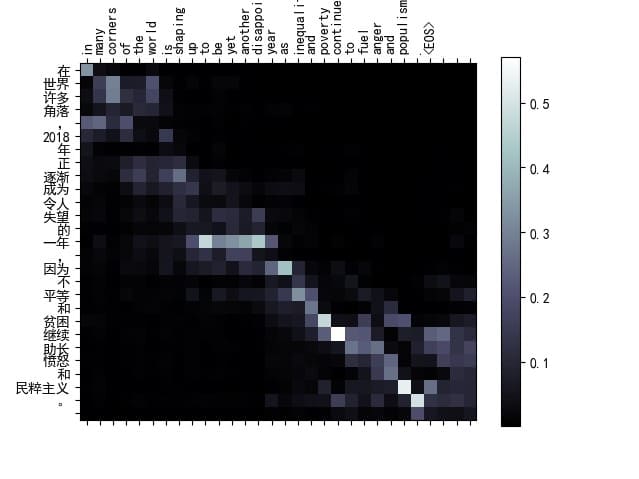
input= 在世界许多角落,2018年正逐渐成为令人失望的一年,因为不平等和贫困继续助长愤怒和民粹主义。
target= in many corners of the world is shaping up to be yet another disappointing year as inequality and poverty continue to fuel anger and populism .
output= in many corners of the world is shaping up to be yet another disappointing year as inequality and poverty continue to fuel anger and populism . <EOS>
BLEU score = 1
该示例展示了模型在处理复杂句子结构时的优秀表现。注意力矩阵显示,模型能够在多个短语之间准确地分配注意力。例如,“不平等”和“inequality”之间的对应关系,以及“愤怒和民粹主义”和“anger and populism”之间的对应关系,都显示出较高的注意力权重
可视化结果4
1
2
3
4
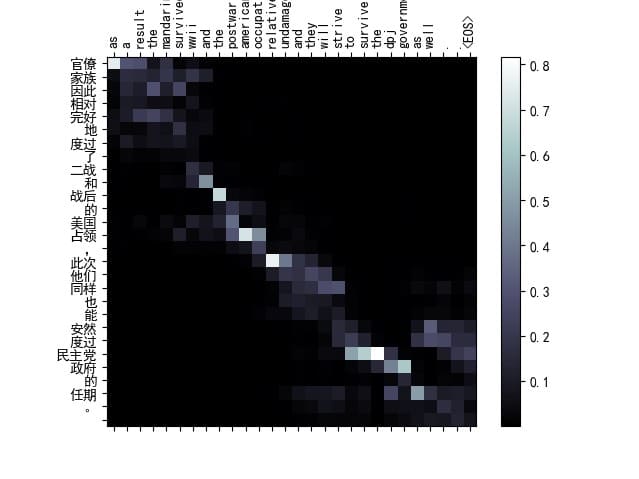
input= 官僚家族因此相对完好地度过了二战和战后的美国占领,此次他们同样也能安然度过民主党政府的任期。
target= as a result the mandarins survived wwii and the postwar american occupation relatively undamaged and they will strive to survive the dpj government as well .
output= as a result the mandarins survived wwii and the postwar american occupation relatively undamaged and they will strive to survive the dpj government as well . <EOS>
BLEU score = 1
这个例子中可以明显的看到由于中英文的语序不同,模型在对齐时并不是每个词语都能精确对应,然而,可以看到,对于关键词语(如“战后-postwar”、“美国-America”)以及它们的周围词,注意力权重较高,说明模型在捕捉这些重要信息时具有较好的表现。
一个自然的疑问是,Attention机制如此有效,那么我们可不可以去掉模型中的RNN部分,仅仅利用Attention呢? 谷歌在Attention is All you need中提出的self-attention机制及Transformer架构回答了这个问题
训练seq2seq模型技巧
-
初始化用Xaiver不如用kaiming初始化好
-
选择合适的优化器: 使用SGD(随机梯度下降)时,训练的loss很难降下来。即使训练了300个epoch,loss仍保持在4左右。然而,使用Adam优化器时,训练到40个epoch时,loss已经下降到1以下。Adam优化器结合了动量和自适应学习率,能够更快地找到全局最优解。
-
动态调整学习率: 可以在训练初期使用较大的学习率,加快模型收敛速度,然后逐渐降低学习率,避免在接近最优解时出现震荡。例如,可以使用学习率调度器(如学习率衰减策略)或自适应学习率算法(如Adam)。
- 使用教师强制训练: 教师强制(Teacher Forcing)在训练过程中将真实的目标序列作为输入给解码器,可以加速模型收敛。同时可以逐步减少其使用,转向自由运行Free Running,以提高模型的鲁棒性。
- 应用L2正则化和Dropout: 为了防止模型过拟合,可以应用L2正则化(权重衰减)和Dropout技术。在RNN中,使用变分Dropout(Variational Dropout)可以进一步增强模型的泛化能力。
- 使用预训练的词向量(如Word2Vec、GloVe或FastText)进行词向量初始化,可以提高模型的表示能力和性能。
- 通过网格搜索或随机搜索进行超参数调优,找到最优的超参数组合,如隐藏层大小、批量大小、学习率等。
结果
由于训练集较小,BLEU>0.03 就被视作正常分数,以下黑色加粗为超过0.03的模型,以下都为训练300个epoch时结果。 100k的数据在300个epoch时loss其实还没收敛,还可以继续训练
GRU_T_G_Bah表示模型使用GRU,训练时用==T==eacher Forcing,解码时用==Greedy== Search,注意力是==Bah==danau attention
LSTM_F_B_Luong表示模型使用LSTM,训练时用==F==ree Running,解码时用==B==eam Search,注意力是==Luong== attention
| 模型 | 测试集BLEU | 训练集BLEU |
|---|---|---|
| GRU_T_G_Bah | 0.07 | 0.31 |
| GRU_T_B_Bah | 0.11 | 0.39 |
| GRU_F_G_Bah | 0.009 | 0.24 |
| GRU_F_B_Bah | 0.012 | 0.28 |
| GRU_T_G_Luong | 0.12 | 0.62 |
| ==GRU_T_B_Luong== | ==0.14== | ==0.66== |
| GRU_F_G_Luong | 0.008 | 0.04 |
| GRU_F_B_Luong | 0.014 | 0.11 |
| LSTM_T_G_Luong | 0.01 | 0.02 |
| LSTM_T_B_Luong | 0.02 | 0.05 |
| GRU_T_G_Luong_100k | 0.095 | 0.34 |
| GRU_T_B_Luong_100k | 0.11 | 0.36 |
| LSTM_T_G_Luong_100k | 0.082 | 0.28 |
| LSTM_T_B_Luong_100k | 0.087 | 0.32 |
可以发现都需要Teacher ForcingBLEU分数才比较高
由于所有的checkpoints加起来有1G多,所以压缩包中只保留了部分checkpoints,所有已训练的checkpoints可在下面这里找到: 链接:https://pan.baidu.com/s/1mfE_ukjrGlU9a69DmbP6bQ?pwd=SYSU 提取码:SYSU
心得体会
在本次实验中,首先需要搭建一个基础的Seq2Seq模型,并在此基础上实现了attention机制。虽然模型搭建过程相对简单,但理解Seq2Seq与attention的核心思想是关键。在数据预处理方面,我遇到了一些挑战。最初的方法效果并不理想,经过多次尝试和改进,最终在训练集上的BLEU分数才提升到0.1以上。
模型训练过程中,我应用了Teacher Forcing策略,这大大加快了模型的收敛速度。Teacher Forcing策略在训练时使用真实的目标序列作为下一步的输入,而不是模型自身预测的结果,这样可以有效缓解梯度消失问题,提升模型性能。然而,过高的Teacher Forcing Ratio可能导致模型过度依赖真实序列,在实际应用中表现不稳定。因此,我在实验中选择了适中的Teacher Forcing Ratio,以在收敛速度和模型鲁棒性之间取得平衡。
此外,我还尝试了不同的解码策略,包括贪婪解码(Greedy Decoding)和束搜索解码(Beam Search)。贪婪解码虽然实现简单且计算效率高,但容易错过更优的序列。相比之下,束搜索解码通过在每一步保留多个最优候选,可以获得更好的解码效果,但计算复杂度较高。
在整个实验过程中,我不仅深入理解了Seq2Seq和attention机制,还实践了许多NLP中的常见方法,例如Teacher Forcing和Beam Search。通过亲身实践课堂上学习的理论知识,我对这些方法的理解和掌握都得到了显著提升。
文档写得比较详细,便于日后的自我复盘与温习。学期结束后整理时会将本篇文章发表于个人博客,作为学习旅程的印记。
参考资料
seq2seq 机器翻译教程 (来自 pytorch 官方教程,需对数据预处理方式进行更改)
分词工具使用:
参考论文 :
Bahdanau 原版 seq2seq+attention 论文 (ICLR2015):Neural Machine Translation by Jointly Learning to Align and Translate
真正的完全图解Seq2Seq Attention模型_seq-seq-CSDN博客
NLP+词法系列(一)︱中文分词技术小结、几大分词引擎的介绍与比较_词法分析技术的选择与比较-CSDN博客


