
Pattern Recognition
HW3 半监督图像分类
Mixmatch & Fixmatch
Student ID: 21307381 Student Name: LJW
Date: 2024.6.18
Lectured by: Jinhua Ma
Pattern Recognition
Sun Yat-sen University
作业介绍
实验目的
关于半监督学习
神经网络模型通常需要大量标记好的训练数据来训练模型。然而,在许多情况下,获取大量标记好的数据可能是困难、耗时或昂贵的。这就是半监督学习的应用场景。 半监督学习的核心思想是利用无标记数据的信息来改进模型的学习效果。在半监督学习中,我们使用少量标记数据进行有监督学习,同时利用大量无标记数据的信息。通过充分利用无标记数据的潜在结构和分布特征,半监督学习可以帮助模型更好地泛化和适应未标记数据。 关于深度学习中半监督学习更全面的总结,可以参考深度学习半监督学习综述[1]
半监督图像分类
半监督学习在图像分类取得了非常大的进步,涌现了许多经典的半监督图像分类算法,如:π Model[2], Mean Teacher[3], MixMatch[4], FixMatch[5]等。这些算法都取得了非常好的结果,能够在仅使用少量标注数据的情况下,实现高精度的图像分类,在 ImageNet, CIFAR-10, CIFAR-100 等数据集上都有非常不错的效果。 TorchSSL[6]是微软发布的一个用于半监督深度学习的库,其中提供了许多半监督学习算法的实现,如下图所示:
实验内容
一、基于 MixMatch 的 CIFAR-10 数据集半监督图像分类
MixMatch 采用两种方式来利用无标注数据,即熵最小化和一致性正则化。 具体来说, MixMatch 首先对无标注数据进行 K 次增强,并获得对应的 K 个输出,并计算模型平均的预测分布,之后, MixMatch 使用一个”sharpening”函数来对无标注数据的平均预测进行锐化,并把锐化后的预测分布作为该无标注数据的标签。获得对无标注数据的标签后,将标注数据和无标注数据结合起来,通过 Mixup 的方式完成新数据集的构建,最后使用新的数据集进行训练。
二、基于 FixMatch 的 CIFAR-10 数据集半监督图像分类
FixMatch 结合了伪标签和一致性正则化来实现对无标注数据的高效利用, 训练过程包括两个部分,有监督训练和无监督训练。有标注的数据,执行有监督训练,和普通分类任务训练没有区别。没有标注的数据,首先将其经过弱增强之后送到模型中推理获取伪标签,然后再将其经过强增强送到模型中进行预测,并利用生成的伪标签监督模型对强增强数据的预测。模型对弱增强数据的预测,只有大于一定阈值条件时才执行伪标签的生成,并使用该伪标签来进行无标注图像的训练。
实验要求
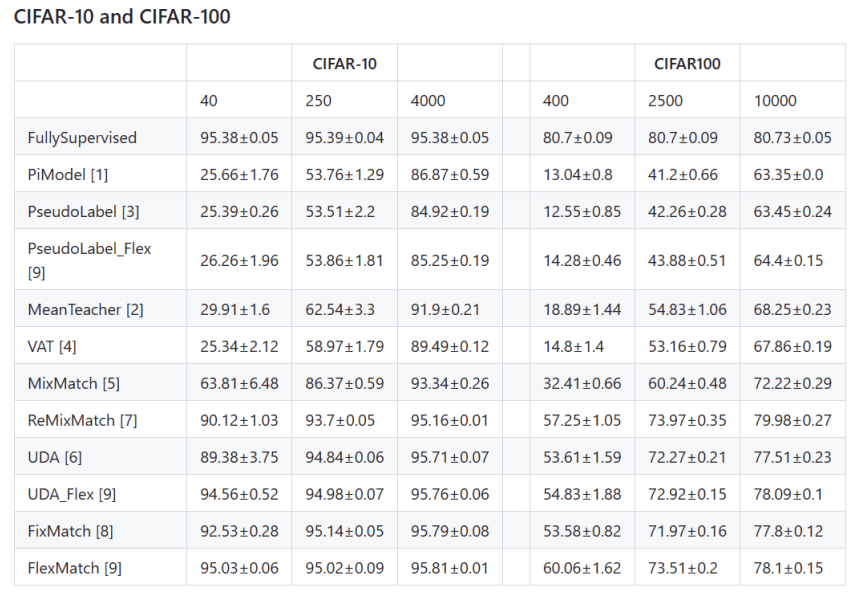
- 阅读原始论文和相关参考资料,基于 Pytorch 分别实现 MixMatch 和 FixMatch半监督图像分类算法, 按照原始论文的设置, MixMatch 和 FixMatch 均使用WideResNet-28-2 作为 Backbone 网络,即深度为 28,扩展因子为 2, 在CIFAR-10 数据集上进行半监督图像分类实验, 报告算法在分别使用 40, 250,4000 张标注数据的情况下的图像分类效果(标注数据随机选取指定数量)
- 使用 TorchSSL[6]中提供的 MixMatch 和 FixMatch 的实现进行半监督训练和测试, 对比自己实现的算法和 TorchSSL 中的实现的效果
- 提交源代码, 不需要包含数据集, 并提交实验报告, 实验报告中应该包含代码的使用方法, 对数据集数据的处理步骤以及算法的主要实现步骤,并分析对比 MixMatch 和 FixMatch 的相同点和不同点
硬性要求 :
- 鉴于部分同学没有GPU可以使用,统一要求训练的迭代数为20000和batch大小为64,所有报告结果都是基于此设置。
- 报告中必须包含对MixMatch和FixMatch方法的解读(结合代码)
- 上述要求内容全部完成
加分项
- 可以完成GPU环境的配置,并成功用于加速训练(需要CPU,GPU训练时长比较与截图)
- 对方法中的组件进行细致的分析,采取不同超参数对准确率的影响
数据处理
Mixmatch和Fixmatch中的数据抽取方式如下:
每个类带标签数据的个数是均衡的,每个类带标签的数据个数 = 带标签数据总个数//类数。所以,使用一个循环(10个类):对于每一个类,找出它们在总数据(labels)中的数据索引,并用Sampler随机选择label_per_class个数据,它们加入到带标签的数据索引labeled_idx中。对于不带标签的数据,使用了所有的数据(包含带标签的数据),所以它的索引为全部数据的索引。
1
2
sampler_x = RandomSampler(ds_x, replacement=True, num_samples=n_iters_per_epoch * batch_size)
batch_sampler_x = BatchSampler(sampler_x, batch_size, drop_last=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def load_data_train(L, dspth='./data'):
"""
加载训练数据集并进行预处理
参数:
L (int): 标签数量
dspth (str): 数据集路径
返回:
data_x, label_x, data_u, label_u: 已处理的训练数据和标签
"""
# 构建训练数据文件列表
datalist = [
osp.join(dspth, 'cifar-10-batches-py', 'data_batch_{}'.format(i+1))
for i in range(5)
]
data, labels = [], []
# 逐个读取数据文件并加载数据
for data_batch in datalist:
with open(data_batch, 'rb') as fr:
entry = pickle.load(fr, encoding='latin1')
lbs = entry['labels'] if 'labels' in entry.keys() else entry['fine_labels']
data.append(entry['data'])
labels.append(lbs)
data = np.concatenate(data, axis=0) # 合并数据
labels = np.concatenate(labels, axis=0) # 合并标签
n_labels = L // 10 # 每个类别的标签数量
data_x, label_x, data_u, label_u = [], [], [], []
for i in range(10): # 遍历每个类别
indices = np.where(labels == i)[0]
np.random.shuffle(indices) # 随机打乱索引
inds_x, inds_u = indices[:n_labels], indices[n_labels:]
data_x += [
data[i].reshape(3, 32, 32).transpose(1, 2, 0)
for i in inds_x
]
label_x += [labels[i] for i in inds_x]
data_u += [
data[i].reshape(3, 32, 32).transpose(1, 2, 0)
for i in inds_u
]
label_u += [labels[i] for i in inds_u]
return data_x, label_x, data_u, label_u # 返回处理后的数据和标签
Mixmatch
数据集:CIFAR-10 数据集由 10 个类别的 60000 个 32x32 彩色图像组成,每个类别包含 6000 个图像。有 50000 个训练图像和 10000 个测试图像。 数据集下载地址:CIFAR-10 and CIFAR-100 datasets (toronto.edu)
MixMatch抓住了半监督算法的三个重要观点:第一是熵最小化;第二是一致性正则化,第三是一般正则化。结合这三个观点的算法就形成了MixMatch。一般正则化也就是使用L2范数,下面介绍熵最小化和一致性正则化。
熵最小化:
在许多半监督学习方法中,一个常见的基本假设是分类器的决策边界不应通过边缘数据分布的高密度区域。这句话简单的理解可以想象一个聚类模型,其决策边界一定是在簇与簇之间的稀疏边界上,不可能穿过一个簇的中心(高密度区域)。而实现这一点的一种方法就是要求分类器对未标记数据输出低熵预测。MixMatch中使用一个”sharpening”函数来隐式实现熵最小化。所谓熵最小化、低熵预测,都是指使输出概率分布比较有“偏向性”,而不希望输出一个“平均的预测”。熵在信息论中是不确定度的度量,根据离散模型的熵最大定理,可知在均匀分布时熵取得最大值,换句话说,出现一个确定的分布,即某一类的概率是1,其余类的概率是0时,熵为0。也就是说想要得到熵最小,就得使分类器输出后的模型预测概率集中分配给某一类。后面再介绍“sharpening”函数如何实现这一点。
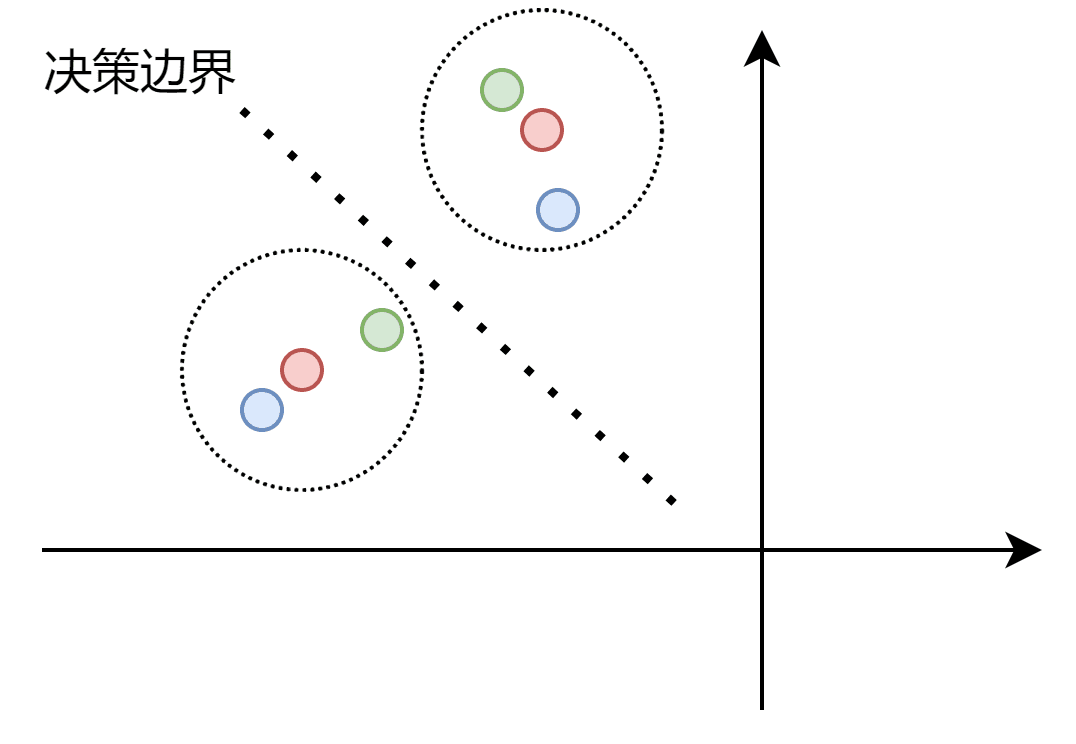
一致性正则化: 一致性正则化也是一个常见的半监督假设。VAT、MeanTeacher等其实都或多或少使用了这种假设。其核心在于,我们希望一个样本和其加扰版本(通常图像中称为Augment)通过分类器后,得到相似的输出。其实也就是说分类边界不应该穿过数据分布的高密度区域。如下图,红色点是原始样本,蓝色和绿色为其扰动版本,红色同心圆的虚线圆是我们期望的容差范围,即在这个区间类的都应该认为和其中心数据点为同一类。通过扰动数据点的加入,将决策边界推到合适的位置,使分类器的鲁棒性更强。
MixMatch 还使用了 Mixup,也就是会将图像拼接在一起,例如我们输入一张一半是猫一半是狗的图像(通过叠加图像或将它们并排放置在图像中),并期望模型产生 p(dog)=.5、p(cat)=.5 以及其余类别的概率 0。可以这样理解:MixMatch 是对之前来出现的几种技术的组合和改进。我认为 MixMatch 论文的神奇之处在于他们找到了一种合理的方法来组合使用以上之前已经提出的思想!
接下来我将先大致说明主要算法流程,然后结合我实现的代码详细分析。
- 数据增强
- 标签猜测生成伪标签
- Mixup
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def mixmatch():
model, Loss_x, Loss_u = set_model(device)
n_iters_per_epoch = n_imgs_per_epoch // batchsize
# 第一步:对数据进行增强
dataloader_train_x, dataloader_train_x = LoadAndAugment_Val(
batchsize, n_iters_per_epoch, L=n_labels, K=n_guesses, root=data_path
)
# 第二步:标签猜测 + Sharpening
lb_guessor = GuessAndSharpening(model, T=temperature)
# 第三步:MixUp,将有标签数据和无标签数据进行混合
mixuper = MixUp(mixup_alpha)
# 第四步:论文中参考Mean Teacher的EMA方法,我也模仿论文中的EMA方法,使用EMA方法进行参数更新
ema = EMA(model, ema_alpha) # 创建EMA对象
...
...
第一步:数据增强
第一步,正如许多SSL方法中的典型做法一样,对数据进行数据增强(Augment)。分别在有标记数据集$X$和无标记数据集$U$上进行增强,分别记为$\hat{X}=Augument(X)$ 和$ \hat{U} =Augument(U)$。对$X$中每一个数据$x_b$进行一次数据增强,对$U$中每个数据$u_b$进行$K$次数据增强,文章中取$ K=2$。之后还会使用这些单独的增强为每个$u_b$生成一个“猜测标签”$q_b$,但这都是后话了。
具体到代码上
1
2
3
4
# 第一步:对数据进行增强
dataloader_train_x, dataloader_train_x = LoadAndAugment_Val(
batchsize, n_iters_per_epoch, L=n_labels, K=n_guesses, root=data_path
)
其中对数据进行增强部分如下:
首先定义数据增强的方法(具体的函数例如RandomHorizontalFlip可见Fixmatch的数据增强部分):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Cifar10Augment(Dataset):
"""
CIFAR-10数据集的自定义Dataset类。
"""
def __init__(self, data, labels, n_guesses=1, is_train=True):
super(Cifar10Augment, self).__init__()
self.data, self.labels = data, labels
self.n_guesses = n_guesses
assert len(self.data) == len(self.labels)
assert self.n_guesses >= 1
# 数据预处理和增强
mean, std = (-0.0172, -0.0356, -0.1069), (0.4940, 0.4869, 0.5231) # [-1, 1]
if is_train:
self.trans = T.Compose([
T.Resize((32, 32)),
T.PadandRandomCrop(border=4, cropsize=(32, 32)),
T.RandomHorizontalFlip(p=0.5),
T.Normalize(mean, std),
T.ToTensor(),
])
else:
self.trans = T.Compose([
T.Resize((32, 32)),
T.Normalize(mean, std),
T.ToTensor(),
])
def __getitem__(self, idx):
im, lb = self.data[idx], self.labels[idx]
ims = []
# 对每个样本进行n_guesses次预处理和增强
for _ in range(self.n_guesses):
im_trans = self.trans(im)
ims.append(im_trans)
return ims, lb
之后对$X$中每一个数据$x_b$进行一次数据增强,对$U$中每个数据$u_b$进行$K$次 数据增强
1
2
3
4
5
6
7
8
9
10
11
12
13
# 创建有标签数据集和无标签数据集
dataset_x = Cifar10Augment(
data=data_x,
labels=label_x,
n_guesses=1, #有标记只进行一次增强
is_train=True
)
dataset_u = Cifar10Augment(
data=data_u,
labels=label_u,
n_guesses=K,
is_train=True
)
第二步:进行标签猜测生成伪标签
1
2
# 第二步:标签猜测 + Sharpening
lb_guessor = GuessAndSharpening(model, T=temperature)
对于U中每个未标记的示例,MixMatch使用模型的预测为该示例的标签生成一个“猜测”。为此,我们通过$u_b$ 的所有K个增量计算模型的预测类分布的平均值。通过如下公式计算,其中$ (\hat{u_{b,k}},y)$是$ \hat{U} $ 的一个Batch:
\[\bar{q_b}=\frac{1}{K}\sum_kP_{model}(y|\hat{u_{b,k}};\theta)\]值得注意的是,$P_{model}(y\mid \hat{u_{b,k}};\theta)$是Softmax之后的预测概率分布。
具体到代码上即为
1
2
3
4
5
6
7
8
9
10
11
...
# guess
all_probs = [] # 用于存储所有样本的类别概率
for im in ims: # ims (list of torch.Tensor): 输入的图像数据列表
if use_gpu:
im = im.cuda() # 将图像数据移动到GPU上
logits = self.guessor(im) # 使用模型进行前向传播,得到logits
probs = torch.softmax(logits, dim=1) # 对logits进行softmax操作,得到预测类别概率
all_probs.append(probs) # 将类别概率添加到列表中
qb = sum(all_probs) / len(all_probs) # 对所有样本的类别概率进行求和并取平均
...
之后给定对增幅$q_b$的平均预测,我们应用锐化函数来减少标签分布的熵:
\[Sharpen(p,T)_i=\frac{p_i^{\frac{1}{T}}}{\sum^L_{j=1}p_j^{\frac{1}{T}}}\]当超参数$ T\to 0$时,$Sharpen(p,T)$趋向于one-hot分布,即其中一个类别的概率为1,其余概率为0;锐化后的概率分布作为$\hat{U} $的数据伪标签(pseudo label)。
具体到代码上:
1
2
3
4
5
...
# sharpen
lbs_tem = torch.pow(qb, 1. / self.T) # 对概率进行温度调节
lbs = lbs_tem / torch.sum(lbs_tem, dim=1, keepdim=True) # 对概率进行归一化,得到伪标签
...
结合起来得到完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import torch
# 这个标签猜测器通过对无标签样本的预测结果进行温度调节,生成伪标签,用于无监督学习中的训练。
use_gpu = False # 设置是否使用GPU
class GuessAndSharpening(object):
def __init__(self, model, T):
"""
初始化标签猜测器
参数:
- model (torch.nn.Module): 用于进行标签猜测的模型
- T (float): softmax温度参数
"""
self.T = T # softmax温度参数
self.guessor = model # 用于进行标签猜测的模型
@torch.no_grad()
def __call__(self, model, ims):
"""
进行标签猜测
参数:
- model (torch.nn.Module): 要进行标签猜测的模型
- ims (list of torch.Tensor): 输入的图像数据列表
返回:
- lbs (torch.Tensor): 伪标签,形状为[batch_size, num_classes]
"""
# guess
org_state = {
k: v.clone().detach()
for k, v in model.state_dict().items()
} # 备份模型当前状态
is_train = self.guessor.training # 记录模型当前是否处于训练状态
self.guessor.train() # 将模型设置为训练模式
all_probs = [] # 用于存储所有样本的类别概率
for im in ims:
if use_gpu:
im = im.cuda() # 将图像数据移动到GPU上
logits = self.guessor(im) # 使用模型进行前向传播,得到logits
probs = torch.softmax(logits, dim=1) # 对logits进行softmax操作,得到类别概率
all_probs.append(probs) # 将类别概率添加到列表中
qb = sum(all_probs) / len(all_probs) # 对所有样本的类别概率进行求和并取平均
# sharpen
lbs_tem = torch.pow(qb, 1. / self.T) # 对概率进行温度调节
lbs = lbs_tem / torch.sum(lbs_tem, dim=1, keepdim=True) # 对概率进行归一化,得到伪标签
self.guessor.load_state_dict(org_state) # 恢复模型之前的状态
if is_train:
self.guessor.train() # 如果之前处于训练状态,则重新设置为训练模式
else:
self.guessor.eval() # 如果之前处于评估状态,则设置为评估模式
return lbs.detach() # 返回伪标签,使用detach()方法使其与计算图脱离,避免梯度传播
第三步:Mixup
1
2
# 第三步:MixUp,将有标签数据和无标签数据进行混合
mixuper = MixUp(mixup_alpha)
第三步,通过MixUp完成新数据集的构建。先将第一步增强后的$\hat{X} $和$\hat{U} $进行拼接再打乱顺序,得到$W=Shuffle(Concat(\hat{X},\hat{U}))$,然后再将$W$分为两部分,第一部分大小与$\hat{X}$ 相同(也与$X$相同),记为$ W_x$;第二部分大小与$\hat{U} $相同(也与U UU相同),记为$W_u$ 。然后将$W_x$和$\hat{X}$ 进行MixUp,$W_u$和$\hat{U}$ 进行MixUp,得到$X’$和$ U’$。MixUp步骤如下:
\[λ ∼ Beta ( α , α ) \\ λ ′ = max ( λ , 1 − λ ) \\ x ′ = λ ′ x 1 + ( 1 − λ ′ ) x 2 \\ p ′ = λ ′ p 1 + ( 1 − λ ′ ) p 2\]其中α是超参数,具体到代码上即为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import torch
use_gpu = False # 设置是否使用GPU
class MixUp(object):
def __init__(self, alpha):
"""
- alpha (float): MixUp参数,控制混合程度
"""
self.beta_generator = torch.distributions.beta.Beta(alpha, alpha)
def __call__(self, ims, lbs):
bs = ims.size(0) # 获取batch_size
if use_gpu:
lam = self.beta_generator.sample([bs, 1, 1, 1]).cuda() # 从Beta分布中采样生成混合比例lam
else:
lam = self.beta_generator.sample([bs, 1, 1, 1])
lam = torch.where(lam > (1. - lam), lam, (1. - lam)) # 将lam限制在[0.5, 1.0]之间
indices = torch.randperm(bs) # 生成随机排列的索引
ims = lam * ims + (1. - lam) * ims[indices] # 进行MixUp操作,线性插值
lam = lam.view(-1, 1) # 将lam转换成[batch_size, 1]的形状
lbs = lam * lbs + (1. - lam) * lbs[indices] # 对标签进行MixUp操作,线性插值
return ims.detach(), lbs.detach() # 返回增强后的图像数据和标签数据,使用detach()方法使其与原数据脱离计算图,避免梯度传播
第四步:计算半监督损失函数
第四步是计算半监督损失函数后反向传播,分为在标记数据集$ X’$上的损失函数$L_x$和在无标记数据集$U’$ 上的损失函数$ L_u$,公式如下:
\[\mathrm{L_{x}=\frac{1}{|X^{\prime}|}\sum_{x,p\in X^{\prime}}H(p,P_{model}(y|x;\theta))}\\\mathrm{L_{u}=\frac{1}{L|U^{\prime}|}\sum_{u,q\in U^{\prime}}||q-P_{model}(y|u;\theta)||_{2}^{2}}\\\mathrm{L=L_{x}+\lambda_{U} L_{u}}\]其中$H(\cdot)$是CorssEntropyLoss;$L_u$是MSE Loss,反向梯度传播即可完成整个MixMatch算法。
具体到代码上即为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
...
Loss_x = CrossEntropyLoss().to(device) # 使用交叉熵损失函数
Loss_u = nn.MSELoss().to(device) # 使用均方误差损失函数
...
optim.zero_grad() # 梯度清零
logits = model(ims) # 输入模型进行前向传播
logits_x = logits[:batchsize] # 获取有标签数据的输出结果
lbs_x = lbs[:batchsize] # 获取有标签数据的标签
logits_u = logits[batchsize:] # 获取无标签数据的输出结果
preds_u = torch.softmax(logits_u, dim=1) # 对无标签数据进行softmax操作
lbs_u = lbs[batchsize:] # 获取无标签数据的标签
loss_x = Loss_x(logits_x, lbs_x) # 计算有标签数据的损失
loss_u = Loss_u(preds_u, lbs_u) # 计算无标签数据的损失
lam_u = lambda_u + lambda_u_once * it # 计算无标签数据的损失权重
loss = loss_x + lam_u * loss_u # 计算总损失
loss.backward() # 反向传播
optim.step() # 更新模型参数
do_weight_decay(model, wd) # 权重衰减
ema.update_params() # 更新EMA参
EMA指数平均
虽然论文中算法描述没有具体提到使用EMA,但是Ablation Study消融学习的时候提到using an exponential moving average (EMA) of model parameters when producing guessedlabels, as is done by Mean Teacher [44]
所以我也参考论文中方法实现了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
import torch
import torch.distributed as dist
'''
这个类实现了指数移动平均(EMA)方法,用于在训练过程中平滑模型参数。
它会记录模型参数的当前状态,并根据衰减率将其更新到影子副本中,
然后在训练过程中使用影子副本来计算损失和梯度,以减少参数更新的方差,从而提高模型的泛化能力。
'''
class EMA(object):
def __init__(self, model, alpha):
"""
初始化EMA对象
参数:
- model (torch.nn.Module): 要应用EMA的模型
- alpha (float): EMA的衰减率,控制新旧参数的权重
"""
self.step = 0 # 当前训练步数
self.model = model # 要应用EMA的模型
self.alpha = alpha # EMA的衰减率
self.shadow = self.get_model_state() # 创建模型参数的影子副本
self.backup = {} # 用于备份模型参数的字典
self.param_keys = [k for k, _ in self.model.named_parameters()] # 获取模型参数的键列表
self.buffer_keys = [k for k, _ in self.model.named_buffers()] # 获取模型缓冲区的键列表
def update_params(self):
"""
更新EMA的参数
"""
decay = min(self.alpha, (self.step + 1) / (self.step + 10)) # 计算衰减因子
state = self.model.state_dict() # 获取模型的当前状态
for name in self.param_keys:
# 使用EMA公式更新参数的影子副本
self.shadow[name].copy_(
decay * self.shadow[name] + (1 - decay) * state[name]
)
self.step += 1 # 更新步数
def update_buffer(self):
"""
更新EMA的缓冲区
"""
state = self.model.state_dict() # 获取模型的当前状态
for name in self.buffer_keys:
# 使用当前状态更新缓冲区的影子副本
self.shadow[name].copy_(state[name])
def apply_shadow(self):
"""
将EMA的参数应用到模型中
"""
self.backup = self.get_model_state() # 备份模型当前的参数状态
self.model.load_state_dict(self.shadow) # 将EMA的影子副本加载到模型中
def restore(self):
"""
恢复模型参数为备份状态
"""
self.model.load_state_dict(self.backup) # 将模型的参数恢复为备份状态
def get_model_state(self):
"""
获取模型当前状态的副本
"""
return {
k: v.clone().detach() # 使用clone()方法创建参数的副本,并使用detach()方法使其与计算图脱离,避免梯度传播
for k, v in self.model.state_dict().items() # 遍历模型参数的字典,并创建副本
}
实验结果
所有运行的log文件都在附录文件中
为了节约计算资源,对于CPU版本只给出训练一个epoch的时间(1个epoch是1000个iteration),根据一个epoch的时间即可大致推断出完整训练20000个iteration的时间。
训练时间
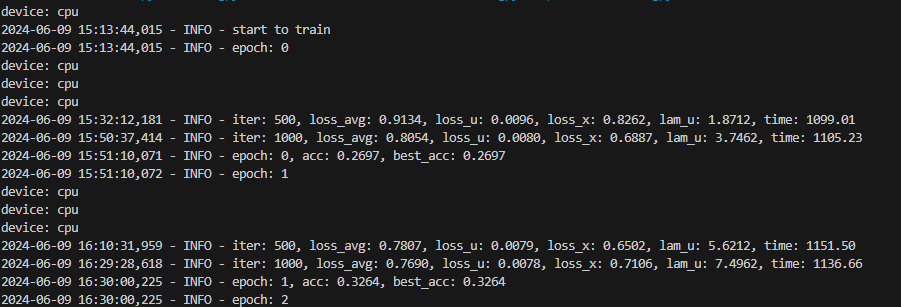
CPU
CPU计算时间:大约2210s一个epoch,训练完20000个iteration(20个epoch)大约需要44200秒=736.6667分钟=12.2778小时:cry:
GPU
GPU计算时间:大约125s一个epoch,训练完20000个iteration(20个epoch)大约需要2500秒=41.6667分钟,相比CPU计算节约了1750%的时间。

TorchSSL
python mixmatch.py –c config/mixmatch/mixmatch_cifar10_250_0.yaml
使用TorchSSL,直接使用给出的默认参数,得到结果如下:
标注数据数量为40时

标注数据数量为250时

标注数据数量为4000时

超参数调整
文中发现 $\alpha = 0.75$ 和 $ \lambda_{\mathcal{U}}=100$是调整的良好起点。
截取TorchSSL中参数设置
mixup_alpha(ulb_loss_ratio) : 0.5
weight_decay: 0.0005
lr: 0.03
temperature(T) : 0.5
lam_u(ulb_loss_ratio) : 100
优化器:SGD
如果我的模型的超参数设置为和TorchSSL一样,那么训练20000iteration时结果与TorchSSL中基本一致,调节之后超参数的结果要优于TorchSSL。
超参数调节
mixup_alpha = 0.75
weight_decay = 0.02
lr = 0.002
temperature = 0.5
lam_u = 75 #无标签数据的损失权重
优化器:Adam
kaiming初始化,且a=0.1时效果远远好于a=0时情况,a=0.1时在第一个epoch就可以达到a=0时8个epoch的情况,且第3个epoch时就可以达到a=0时第18个epoch的情况
最终结果
| 版本/标注数据数量 | 40 | 250 | 4000 |
|---|---|---|---|
| 我的实现(与Torch超参一致) | 0.3379 | 0.6702 | 0.8521 |
| 我的实现 | 0.3998 | 0.7360 | 0.8780 |
| TorchSSL | 0.3159 | 0.6891 | 0.8817 |
之后为了探究我的实现能达到的精度,在标注数据数量为40时进行了探究,参考精度是$63.81\pm6.48$。
-
我用自己实现的版本训练了100个epoch(100 000个iteration),在第53个epoch(53 000个iteration)就达到了0.5833的精度,最终在第70个epoch达到了最高的0.6539(尝试了3次取平均)
-
与之对比的是TorchSSL在标注数据数量为40时,在100 000个iteration时准确率为0.5779,最终在705 000个iteration时达到了最高的0.7。
可以看到我实现的mixmatch是可以达到论文中描述的精度的。
Fixmatch
FixMatch 是 SSL 两种方法的组合: 一致性正则化和伪标签。它的新颖之处在于这两种方法的组合以及在执行一致性正则化时使用单独的弱增强和强增强。一致性正则化就如MixMatch中描述那样。
伪标记(pseudo label)是一种常用的半监督算法。代表算法是self-training。简单地说就是通过训练的模型对无标记样本打标签,这个标签有对有错,通过一些方法筛选标签后,选择一部分无标记样本和模型打的标签一起送入模型继续训练。伪标记的方法最大问题在于,如何保证伪标记的正确性。因为当模型打的标签提供了较多的错误信息时,会使模型的训练结果更劣。一般常见的筛选方式是将模型输出的预测结果(Softmax之后)进行阈值判断,其argmax的概率大于阈值,才认为是有效标记,否则将此无标记样本丢弃。
FixMatch算法并不复杂,由其论文中的流程图就可以很好的理解:将弱增强图像输入模型, 当某一预测类别概率高于阈值(虚线)时,预测将转换为 one-hot 伪标签。 然后,计算模型对同一图像的强增强的预测。计算强增强的预测与伪标签之间的交叉熵损失。
简单而言,Fixmatch的流程可以分为以下五步:
1)计算有标记数据集上的交叉熵损失 $L_s$
2)对无标签样本进行数据增强,增强分为强增强和弱增强。
3)对每一个 $ \mu B$batch, 计算弱增强无标签数据集上的预测分布及伪标签 $q_b$, $\hat{q}_b$
4)计算无标签数据交叉熵损失 $ L_u$
5)得到目标函数总损失 $L_s+\lambda L_u$
接下来我将结合代码具体描述每一个步骤。
第一步:有标记样本训练
对于有标记样本,进行正常的监督学习,损失函数为CrossEntropyLoss,得到$L_s$
\[L_\mathrm{s} = \frac{1}{\mathrm{B}} \sum_{\mathrm{b}=1}^\mathrm{B} \mathrm{B}(\mathrm{p}_\mathrm{b} ,\mathrm{p}_\mathrm{m} (\mathrm{y} |\alpha(\mathrm{x}_\mathrm{b} )))\]1
2
3
4
5
...
logits_x, logits_u = logits_x_u[:n_x], logits_x_u[n_x:]
lbs_x = lbs_x.long()
loss_x = Loss_x(logits_x, lbs_x) # 计算有标签数据的损失
...
第二步 数据增强
对于无标记样本,参照上图,共四步。
第一步,先对无标记样本进行增强(Augment),增强分为强增强和弱增强。
弱增强是一种标准的翻转和移位增强策略。 例如在数据集上以 50% 的概率随机水平翻转图像, 并且在垂直和水平方向上随机平移。
这里的弱增强代码与mixmatch中一致,直接复用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
class PadandRandomCrop(object):
'''
将输入张量期望为形状为(H, W, 3)
'''
def __init__(self, border=4, cropsize=(32, 32)):
self.border = border
self.cropsize = cropsize
def __call__(self, im):
# 添加边界
borders = [(self.border, self.border), (self.border, self.border), (0, 0)]
canvas = np.pad(im, borders, mode='reflect')
H, W, C = canvas.shape
h, w = self.cropsize
# 计算裁剪范围
dh, dw = max(0, H - h), max(0, W - w)
sh, sw = np.random.randint(0, dh), np.random.randint(0, dw)
# 随机裁剪
out = canvas[sh:sh + h, sw:sw + w, :]
return out
class RandomHorizontalFlip(object):
def __init__(self, p=0.5):
self.p = p
def __call__(self, im):
# 随机水平翻转
if np.random.rand() < self.p:
im = im[:, ::-1, :]
return im
class Resize(object):
def __init__(self, size):
self.size = size
def __call__(self, im):
# 调整大小
im = cv2.resize(im, self.size)
return im
class Normalize(object):
'''
输入为像素值范围在[0, 255]之间,通道顺序为'rgb'
'''
def __init__(self, mean, std):
self.mean = np.array(mean, np.float32).reshape(1, 1, -1)
self.std = np.array(std, np.float32).reshape(1, 1, -1)
def __call__(self, im):
if len(im.shape) == 4:
mean, std = self.mean[None, ...], self.std[None, ...]
elif len(im.shape) == 3:
mean, std = self.mean, self.std
# 将像素值归一化到[0, 1]
im = im.astype(np.float32) / 255.
# 像素值标准化
im -= mean
im /= std
return im
class ToTensor(object):
def __init__(self):
pass
def __call__(self, im):
if len(im.shape) == 4:
# 将NumPy数组转换为张量并转置通道
return torch.from_numpy(im.transpose(0, 3, 1, 2))
elif len(im.shape) == 3:
# 将NumPy数组转换为张量并转置通道
return torch.from_numpy(im.transpose(2, 0, 1))
class Compose(object):
def __init__(self, ops):
self.ops = ops
def __call__(self, im):
# 应用所有操作
for op in self.ops:
im = op(im)
return im
对于强增强, 文中尝试了两种基于 AutoAugment 的方法, 然后是 Cutout。AutoAugment 使用强化学习来查找包含来自 Python Imaging Library 的转换的增强策略。这需要标记数据来学习增强策略,这使得在可用标记数据有限的 SSL 设置中使用存在问题。因此, 使用不需要利用标记数据学习增强策略的 AutoAugment 变体,例如 RandAugment 和 CTAugment。RandAugment 和 CTAugment 都没有使用学习策略,而是为每个样本随机选择转换。 对于 RandAugment, 控制所有失真严重程度的幅度是从预定义的范围内随机采样的。具有随机幅度的 RandAugment 也被用于 UDA。而对于 CTAugment,单个变换的幅度是即时学习的。
Cutout
这种增强会随机删除图像的正方形部分,并用灰色或黑色填充。
PyTorch没有内置的Cutout函数,于是我实现代码如下:
1
2
3
4
5
6
7
8
9
10
11
def cutout_func(img, pad_size, replace=(0, 0, 0)):
replace = np.array(replace, dtype=np.uint8)
H, W = img.shape[0], img.shape[1]
rh, rw = np.random.random(2)
pad_size = pad_size // 2
ch, cw = int(rh * H), int(rw * W)
x1, x2 = max(ch - pad_size, 0), min(ch + pad_size, H)
y1, y2 = max(cw - pad_size, 0), min(cw + pad_size, W)
out = img.copy()
out[x1:x2, y1:y2, :] = replace
return out
RandAugment
Random Augmentation(RandAugment) 思想是非常简单的。首先,有一个14种可能的增强的列表,以及一系列可能的幅度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 图像增强函数字典
func_dict = {
'Identity': identity_func,
'AutoContrast': autocontrast_func,
'Equalize': equalize_func,
'Rotate': rotate_func,
'Solarize': solarize_func,
'Color': color_func,
'Contrast': contrast_func,
'Brightness': brightness_func,
'Sharpness': sharpness_func,
'ShearX': shear_x_func,
'TranslateX': translate_x_func,
'TranslateY': translate_y_func,
'Posterize': posterize_func,
'ShearY': shear_y_func,
}
# 默认参数字典
translate_const = 10
MAX_LEVEL = 10
replace_value = (128, 128, 128)
arg_dict = {
'Identity': none_level_to_args,
'AutoContrast': none_level_to_args,
'Equalize': none_level_to_args,
'Rotate': rotate_level_to_args(MAX_LEVEL, replace_value),
'Solarize': solarize_level_to_args(MAX_LEVEL),
'Color': enhance_level_to_args(MAX_LEVEL),
'Contrast': enhance_level_to_args(MAX_LEVEL),
'Brightness': enhance_level_to_args(MAX_LEVEL),
'Sharpness': enhance_level_to_args(MAX_LEVEL),
'ShearX': shear_level_to_args(MAX_LEVEL, replace_value),
'TranslateX': translate_level_to_args(
translate_const, MAX_LEVEL, replace_value
),
'TranslateY': translate_level_to_args(
translate_const, MAX_LEVEL, replace_value
),
'Posterize': posterize_level_to_args(MAX_LEVEL),
'ShearY': shear_level_to_args(MAX_LEVEL, replace_value),
}
然后从这个列表里随机选出N个增强和选择一个随机的幅度M,从1到10。这里我们从列表里选出两种,选择一个幅度10,这意味着以百分比表示的幅度为100%(RandomAugment(2, 10))。
最后,将所选的增强应用于序列中的图像。每种增强都有100%的可能性被应用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class RandomAugment(object):
def __init__(self, N=2, M=10):
self.N = N
self.M = M
# 随机选择N个增强操作
def get_random_ops(self):
sampled_ops = np.random.choice(list(func_dict.keys()), self.N)
return [(op, 0.5, self.M) for op in sampled_ops]
def __call__(self, img):
ops = self.get_random_ops()
for name, prob, level in ops:
if np.random.random() > prob: continue
args = arg_dict[name](level)
img = func_dict[name](img, *args)
img = cutout_func(img, 16, replace_value)
return img
最终弱增强和强增强代码封装如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Cifar10Augment(Dataset):
"""
自定义CIFAR-10数据集类
"""
def __init__(self, data, labels, is_train=True):
super(Cifar10Augment, self).__init__()
self.data, self.labels = data, labels
self.is_train = is_train
assert len(self.data) == len(self.labels) # 确保数据和标签数量相等
mean, std = (0.4914, 0.4822, 0.4465), (0.2471, 0.2435, 0.2616)
# mean, std = (-0.0172, -0.0356, -0.1069), (0.4940, 0.4869, 0.5231) # [-1, 1]
if is_train:
self.trans_weak = T.Compose([
T.Resize((32, 32)),
T.PadandRandomCrop(border=4, cropsize=(32, 32)),
T.RandomHorizontalFlip(p=0.5),
T.Normalize(mean, std),
T.ToTensor(),
])
self.trans_strong = T.Compose([
T.Resize((32, 32)),
T.PadandRandomCrop(border=4, cropsize=(32, 32)),
T.RandomHorizontalFlip(p=0.5),
RandomAugment(2, 10), # 强增强
T.Normalize(mean, std),
T.ToTensor(),
])
else:
self.trans = T.Compose([
T.Resize((32, 32)),
T.Normalize(mean, std),
T.ToTensor(),
])
第三步:对弱增强样本预测生成伪标签
第二步,对增强后的样本进行预测。对于弱增强的样本,输出的预测结果(Softmax之后的)最高预测概率(即argmax的结果)大于阈值(图中的虚线),则认为是有效的样本,将其预测结果转换为one-hot编码作为标签(这就是pseudo label)。
1
lbs_u, valid_u = lb_guessor(model, ims_u_weak) # 使用LabelGuessor预测未标记数据的标签
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import torch
class LabelGuessor(object):
def __init__(self, thresh):
self.thresh = thresh # 设置阈值,用于筛选高置信度的标签
def __call__(self, model, ims):
# 备份模型的当前状态
org_state = {
k: v.clone().detach()
for k, v in model.state_dict().items()
}
# 记录模型当前的训练模式(训练或评估)
is_train = model.training
with torch.no_grad(): # 禁用梯度计算
model.train() # 切换模型到训练模式,以确保BatchNorm和Dropout层的行为一致
all_probs = [] # 初始化一个空列表,用于存储所有的概率
logits = model(ims) # 前向传播,计算模型的输出
probs = torch.softmax(logits, dim=1) # 计算每个类别的概率
scores, lbs = torch.max(probs, dim=1) # 获取每个样本的最高概率和对应的标签
idx = scores > self.thresh # 根据阈值筛选高置信度的样本
lbs = lbs[idx] # 仅保留高置信度样本的标签
# 恢复模型的原始状态
model.load_state_dict(org_state)
if is_train:
model.train() # 恢复训练模式
else:
model.eval() # 恢复评估模式
return lbs.detach(), idx # 返回高置信度样本的标签和索引
第四步:对强增强样本计算交叉熵损失(一致性正则化)
第三步:对强增强的样本,输出的预测结果和对应弱标记样本得到的伪标签做CrossEntropyLoss,得到损失函数$ L_u$ 其公式表达为:
\[L_u=\frac{1}{\mu B}\sum^{\mu B}_{b=1}\mathcal(max(q_b)\geq \tau )H(\hat{q_b},p_m(y|\mathcal{A}(u_b))) \\\]$p_m(y∣x) $为预测类别分布,$\tau$为阈值,鼓励模型的预测是对未标记数据的低熵,或者说是高置信度。μ是一个超参数,它决定批中未标注图像的相对大小,μ=2意味着我们使用的未标注图像数量是标注图像的两倍。我取得是μ=7。
| 结合第三第四步,也就是选择$max(q_b)\geq \tau$的$H(\hat{q_b},p_m(y | \mathcal{A}(u_b)))$作为$L_u$ 的组成成分,参与反向梯度传播更新。 |
1
2
3
4
5
6
logits_x_u = model(ims_x_u)
logits_x, logits_u = logits_x_u[:n_x], logits_x_u[n_x:]
lbs_x = lbs_x.long()
loss_x = Loss_x(logits_x, lbs_x) # 计算有标签数据的损失
loss_u = Loss_u(logits_u, lbs_u) # 计算无标签数据的损失
第五步:最终损失函数
在前面已经使用交叉熵损失在标注的图像上训练了监督模型。对于每个未标注的图像,使用弱增强和强增强获得两个图像。弱增强图像被传递到我们的模型中,我们得到了关于类的预测。将最有信心的类别的概率与阈值进行比较。如果它高于阈值,那么我们将该类作为ground truth的标签,即伪标签。然后,将经过强增强的图像传递到我们的模型中,获取类别的预测。使用交叉熵损失将此概率分布与ground truth伪标签进行比较。两种损失组合起来进行模型的更新。所以最终损失函数为$Loss = L_s+\lambda L_u$,$\lambda$是超参数。对Loss反向梯度传播完成整个算法模型更新。
1
loss = loss_x + lambda_u * loss_u # 总损失
实验结果
所有运行的log文件都在附录文件中
训练时间
CPU
CPU计算时间:大约4200s一个epoch,训练完20000个iteration(20个epoch)大约需要84 000秒= 1400分钟= 23.34小时:cry:

GPU
GPU计算时间:大约400秒一个epoch,训练完20000个iteration(20个epoch)大约需要8000秒=133.34分钟=2.22小时,相比CPU计算节约了1050%的时间。与mixmatch相比时间增加了320%。
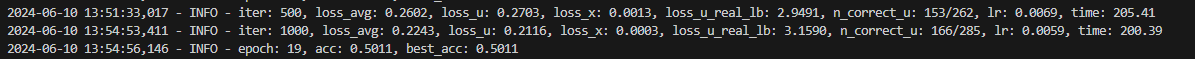
Torch
python fixmatch.py –c config/fixmatch/fixmatch_cifar10_40_0.yaml
标注数据数量为40时:

标注数据数量为250时:
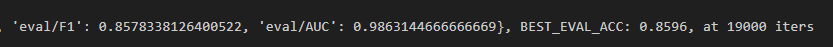
标注数据数量为4000时:
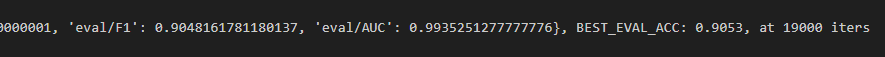
超参数调整
Fixmatch论文发现使用 Adam 优化器会导致更差的性能, 而使用 SGD 则没有这种情况, 另外, 使用 SGD 和使用 Nesterov 之间没有存在实质性差异。
TorchSSL中超参数,括号中是在TorchSSL中命名
mu(uratio) = 7
lam_u(ulb_loss_ratio) = 1.0 # 无标签数据的损失权重
ema_alpha(ema_m) = 0.999 # EMA参数的衰减率
lr = 0.03
weight_decay = 5e-4
momentum = 0.9
我的(经过多番尝试发现修改超参数和TorchSSL一样时性能最好,使用kaiming_normal_时选fan_in比fan_out好很多,a=0比a=0.1)
mu = 7 # μ=2意味着我们使用的未标注图像数量是标注图像的两倍
lam_u = 1.0 # 无标签数据的损失权重
ema_alpha = 0.999 # EMA参数的衰减率
lr = 0.03
weight_decay = 5e-4
momentum = 0.9
初始化方式发现下面这个比较好:
最终结果
| 版本/标注数据数量 | 40 | 250 | 4000 |
|---|---|---|---|
| 我的实现 | 0.5011 | 0.7357 | 0.8939 |
| TorchSSL | 0.4497 | 0.8596 | 0.9053 |
由于Fixmatch训练时间比较久,就不像Mixmatch一样探究最终性能了。(而且发现了标注数据数量大的时候训练时间反而小,不知道是不是因为设备的原因)
MixMatch 和 FixMatch 的相同点和不同点
MixMatch 和 FixMatch 都是半监督学习(SSL)领域的算法,旨在利用少量标记数据和大量未标记数据来训练模型。下面是对这两种算法的相同点和不同点的分析:
相同点:
- 半监督学习目标:两者都旨在解决半监督学习问题,即在有限的标记数据情况下提高模型性能。
- 数据增强:两种方法都使用了数据增强技术来增加数据的多样性,帮助模型学习更鲁棒的特征表示。
- 伪标签:MixMatch 和 FixMatch 都利用了伪标签的概念,即用模型自身的预测结果作为未标记数据的标签,并以此进行训练。
不同点:
- 标签生成策略:
- MixMatch:通过对未标记数据进行多次数据增强,然后取模型预测的均值,并使用一个“锐化”函数来生成低熵的伪标签。
- FixMatch:使用弱增强和强增强的数据样本,只有当弱增强样本的预测概率超过某个阈值时,才会生成伪标签。
- 损失函数设计:
- MixMatch:结合了交叉熵损失和MSE损失,对标记数据和未标记数据分别计算损失,并将它们结合起来。
- FixMatch:使用了交叉熵损失,对未标记数据的损失计算中加入了一个掩码,只更新那些预测概率超过阈值的样本。
- 一致性正则化:
- MixMatch:通过MixUp技术,将标记和未标记数据混合,增强模型的泛化能力。
- FixMatch:虽然也强调了一致性正则化的重要性,但在具体实现上与MixMatch有所不同,见Fixmatch的第四步
- 算法流程:
- MixMatch:算法流程包括数据增强、标签猜测、MixUp混合以及损失函数的计算。
- FixMatch:算法流程则更侧重于伪标签的生成和筛选,以及强、弱增强样本的损失计算。
- 实现复杂度:
- MixMatch:实现相对复杂,涉及到多次数据增强、锐化函数和MixUp操作。
- FixMatch:实现相对简化,重点在于伪标签的生成和筛选过程。
- 超参数:
- MixMatch:有多个超参数,如MixUp中的Beta分布参数、锐化温度等。
- FixMatch:主要的超参数是伪标签生成的阈值和用于未标记样本损失的权重。
- 性能和效率:
- MixMatch:在多个数据集上取得了很好的性能,特别是在标记数据非常有限的情况下,且训练速度快(约120秒训练1000个iteration)。
- FixMatch:效果要优于Mixmatch,但是训练时间要更长,约380秒训练1000个iteration。
如何运行代码
配置好Pytorch环境后,修改下面超参数后运行fixmatch.py或者mixmatch.py即可,主要修改的是data_path和use_gpu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 超参数设置
wresnet_k = 2
wresnet_n = 28
n_classes = 10
n_labeled = 250
n_epoches = 20
batchsize = 64
mu = 7
thr = 0.95
n_imgs_per_epoch = 64 * 1000
lam_u = 1.0
ema_alpha = 0.999
lr = 0.03
weight_decay = 5e-4
momentum = 0.9
seed = -1
sample_interval = 500 # 每500个迭代输出一次训练信息
data_path = '../../Mixmatch/data'
# 全局设置
use_gpu = True
device = torch.device('cuda' if use_gpu else 'cpu') # 设置设备为GPU或CPU
实验感想
本次实验我复现了MixMatch和FixMatch算法,过程充满了挑战和收获。以下是我对本次实验的一些详细感想和总结。
首先,这次实验的难度确实不小,从开始搭建基本结构到最终完成实验,我花费了整整一周时间。MixMatch和FixMatch作为半监督学习的代表算法,它们的实现涉及多个复杂的步骤,包括数据增强、伪标签生成以及损失函数的设计等。刚开始的时候,我对这些步骤的理解还不够深入,因此在代码实现上遇到了不少困难。
在搭建好基本结构之后,调参过程也颇为漫长。半监督学习算法对超参数比较敏感,如学习率、损失权重等都需要细致调整。每次参数调整都需要大量的实验验证,而实验结果的波动性也使得调参过程变得更加复杂。为了得到较好的实验结果,我尝试了多种不同的参数组合,并花费了大量时间进行验证和比较,最终才得到了相对满意的结果。
在实验期间,我还阅读了期末作业中关于开放词汇检测的相关论文,发现其与MixMatch和FixMatch有着异曲同工之妙。开放词汇识别旨在识别或分类训练集中未出现过的类别,这通常需要模型具备强大的泛化能力。在这一领域,伪标签技术同样扮演着关键角色,通过模型初步预测为未标记数据分配临时标签,再将这些数据融入训练过程中,以此迭代优化模型。这种自我训练或迭代增强的方法与MixMatch和FixMatch的核心思想不谋而合,都体现了半监督学习在资源有限情况下的强大适应性和学习能力。通过对比这些方法,我进一步加深了对半监督学习技术的理解。
MixMatch和FixMatch算法的创新之处在于它们如何生成和利用伪标签。例如,FixMatch通过使用强增强和弱增强的样本来生成更可靠的伪标签,而MixMatch则通过MixUp技术来增强模型对未标记数据的泛化能力。这种方法不仅在理论上具有创新性,在实际应用中也展现出了强大的效果。特别是FixMatch,其通过更加简单有效的方式生成伪标签,并在数据增强策略上进行了改进,使得模型在半监督学习任务中的表现更加优越。
总的来说,这次实验让我对半监督学习有了更深刻的认识。从理论学习到实践操作,每一个环节都让我受益匪浅。尽管实验过程中遇到了诸多困难,但正是这些困难促使我不断学习和思考,最终克服了挑战,完成了实验。通过这次实验,我不仅掌握了MixMatch和FixMatch的实现方法,还体会到了科学研究中坚持与探索的重要性。这将对我今后的学习和研究工作带来积极的影响。