
Pattern Recognition
HW2 基于 PCA/LDA 和 KNN 的人脸识别
Student ID: 21307381 Student Name: LJW
Date: 2024.5.25
Lectured by: Jinhua Ma
Pattern Recognition
Sun Yat-sen University
基于 PCA/LDA 和 KNN 的人脸识别
实验目的
-
熟悉并掌握 PCA、 LDA 的基本原理,并应用 PCA 和 LDA 实现数据降维
-
熟悉利用 KNN 分类器对样本进行分类
实验要求
- 提交实验报告,要求有适当步骤说明和结果分析
-
将代码和结果打包提交
- 不能直接调用现有的库函数提供的 PCA、 LDA、 KNN 接口
实验内容
- 自己实现 PCA 和 LDA 数据降维算法以及 KNN 分类器
- 利用实现的两种降维算法对数据进行降维
- 利用降维后的结果,用 KNN 进行训练和测试
实验过程
一. 实现 PCA 函数接口
实现一个你自己的 PCA 函数。 PCA 函数的主要流程是:先对计算数据的协方差矩阵,然后在对协方差矩阵进行 SVD 分解,得到对应的特征值和特征向量。
二. 实现 LDA 函数接口
实现一个你自己的 LDA 函数。 LDA 函数的主要流程是: 将样本数据按照类别进行分组,计算每个类别样本的均值向量。 计算类内散度矩阵与类间散度矩阵,利用二者得到投影矩阵,并用其进行数据降维。
三. 利用数据降维算法对输入数据进行降维
读取 yale face 数据集 Yale_64x64.mat,将数据集划分为训练和测试集,数据集读取划分代码如下。
1
2
3
4
5
6
7
8
from scipy import io
x=io.loadmat('Yale_64x64.mat')
ins_perclass,class_number,train_test_split = 11,15,9
input_dim=x['fea'].shape[1]
feat=x['fea'].reshape(-1,ins_perclass,input_dim)
label=x['gnd'].reshape(-1,ins_perclass)
train_data,test_data = feat[:,:train_test_split,:].reshape(-1,input_dim),feat[:,train_test_split:,:].reshape(-1,input_dim)
train_label,test_label = label[:,:train_test_split].reshape(-1),label[:,train_test_split:].reshape(-1)
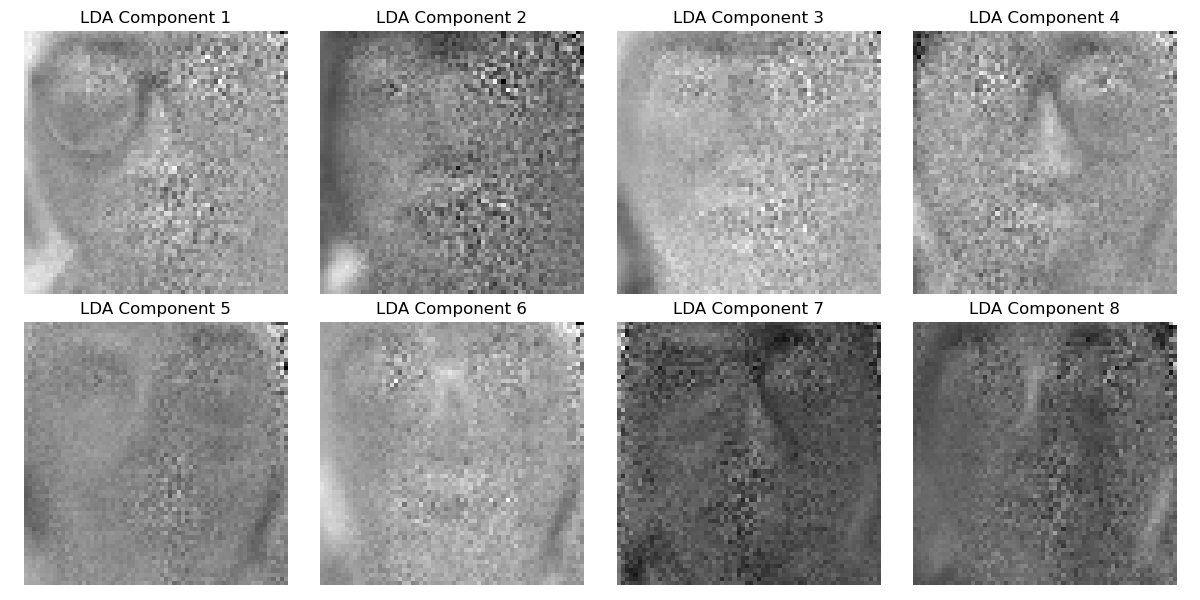
只用训练集数据来学习 PCA 和 LDA 算法中的投影矩阵,并分别将两个方法相应的前 8 个特征向量变换回原来图像的大小进行显示。
然后对训练和测试数据用 PCA 和 LDA 分别进行数据降维(使用所学习的投影矩阵) 。
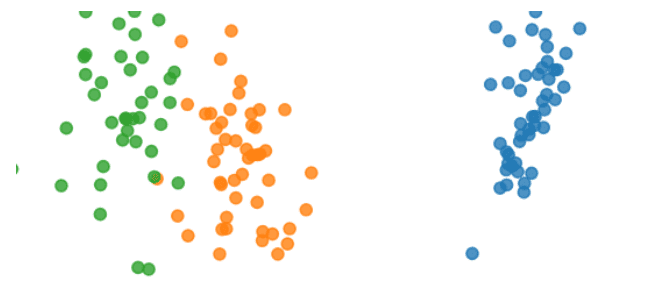
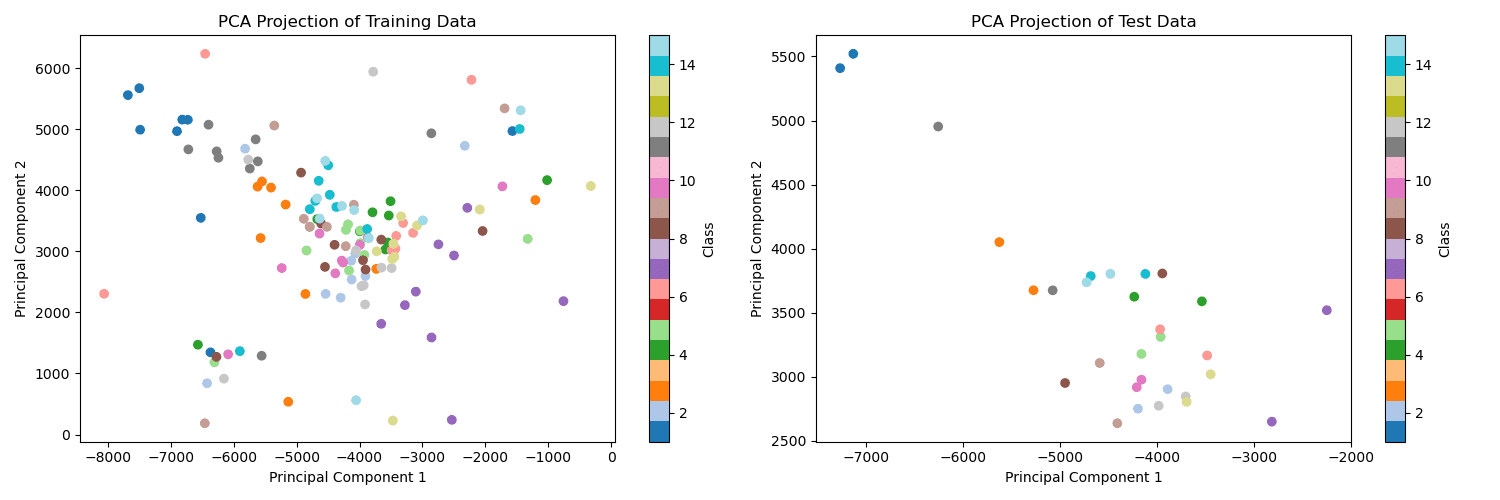
最后对采取 reduced_dim=2,即降维到 2 维后的训练和测试数据进行可视化,展示降维的效果(例如用第一维做 x,第二维做 y,不同类别采用不同颜色绘制散点图,这里只表示三类的情况,报告中应该是 15 个类)
四. 利用 KNN 算法进行训练和测试
利用降维后的训练数据作为 KNN 算法训练数据,降维后的测试数据作为评估 KNN 分类效果的测试集,分析在测试集上的准确率(压缩后的维度对准确率的影响,至少要给出压缩到 8 维的准确率)。
拓展:尝试利用不同的分类器,如 SVM 等达到更好的准确率。此部分允许调库。
实现PCA接口
介绍PCA
PCA(principal component analysis),主成分分析法是一种无监督学习的降维技术,它的目标是将高维数据投影到低维空间中,使得投影后的数据能够保留原始数据的大部分信息。也就是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分(方差最大的方向),是在原有n维特征的基础上重新构造出来的k维特征。
PCA的工作就是从原始的空间中顺序的找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大,第三个轴是与第1、2个轴正交的平面中方差最大的。以此类推,可以得到n个这样的坐标轴。
通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。
所以选择包含最大差异性的主成分方向,也就是计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值特征向量,选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中,实现数据特征的降维。
得到协方差矩阵的特征值特征向量有两种方法:
- 特征值分解协方差矩阵、
- 奇异值分解(SVD)协方差矩阵,
所以PCA算法有两种实现方法:
- 基于特征值分解协方差矩阵实现PCA算法
- 基于SVD分解协方差矩阵实现PCA算法。
接下来我们使用SVD分解实现PCA算法。
SVD的推导见【附录-前驱知识-SVD】
PCA算法流程
PCA可以通过以下几个步骤推导:
输入:数据集 $X={ x_{1},x_{2},x_{3},…,x_{n} }$ ,需要降到k维。
1) 对数据进行中心化处理,即每一位特征减去各自的平均值。
2) 计算数据的协方差矩阵。
3) 通过SVD计算协方差矩阵的特征值与特征向量。
4) 对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵,作为投影矩阵。
5) 将数据转换到k个特征向量构建的新空间中。
基于特征值分解协方差矩阵实现PCA算法时,我们需要找到样本协方差矩阵$ XX^T$ 的最大k个特征向量,然后用这最大的k个特征向量组成的矩阵来做低维投影降维。可以看出,在这个过程中需要先求出协方差矩阵$ XX^T$,当样本数多、样本特征数也多的时候,这个计算还是很大的。当我们用到SVD分解协方差矩阵的时候,SVD有两个好处:
1) 有一些SVD的实现算法可以先不求出协方差矩阵 $XX^T $也能求出我们的右奇异矩阵V。也就是说,我们的PCA算法可以不用做特征分解而是通过SVD来完成,这个方法在样本量很大的时候很有效。实际上,scikit-learn的PCA算法的背后真正的实现就是用的SVD,而不是特征值分解。 1) 注意到PCA仅仅使用了我们SVD的左奇异矩阵,没有使用到右奇异值矩阵,那么右奇异值矩阵有什么用呢?
假设我们的样本是$m\times n$的矩阵X,如果我们通过SVD找到了矩阵$ X^TX$ 最大的k个特征向量组成的$k\times n$的矩阵 $V^T$ ,则我们可以做如下处理:
\[X_{m*k}^{'}=X_{m*n}V_{n*k}^{T}\]可以得到一个$m\times k$的矩阵$X’$,这个矩阵和我们原来$m\times n$的矩阵$X$相比,列数从n减到了k,可见对列数进行了压缩。也就是说,
- 左奇异矩阵可以用于对行数的压缩;
- 右奇异矩阵可以用于对列(即特征维度)的压缩。
这就是我们用SVD分解协方差矩阵实现PCA可以得到两个方向的PCA降维(即行和列两个方向)。
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def PCA(data, n_components):
# 1.对数据进行中心化处理
mean = np.mean(data, axis=0)
centered_data = data - mean
# 2.计算数据的协方差矩阵
cov_matrix = np.cov(centered_data, rowvar=False)
# 3.通过SVD计算协方差矩阵的特征值与特征向量
U, S, Vt = np.linalg.svd(cov_matrix)
# 4.对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵,作为投影矩阵。
components = Vt[:n_components]
# 5. 将数据转换到k个特征向量构建的新空间中
projected_data = np.dot(centered_data, components.T)
return projected_data, components
实现LDA接口
介绍LDA
LDA(Linear Discriminant Analysis),线性判别分析。LDA是一种监督学习的降维技术(与PCA不同)。主要用于数据预处理中的降维、分类任务。LDA的目标是最大化类间区分度的坐标轴成分,将特征空间投影到一个维度更小的k维子空间中,同时保持区分类别的信息。简而言之,LDA投影后不同类别的数据在低维空间中类内方差最小,类间方差最大。
也就是我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
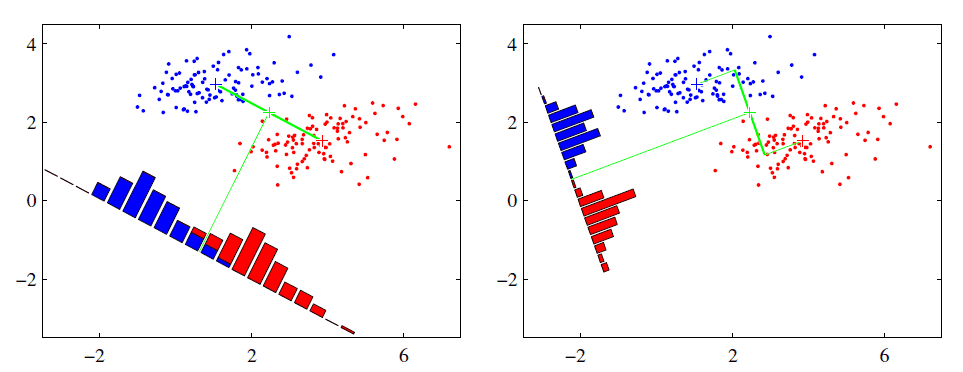
从直观上可以看出,右图要比左图的投影效果好,因为右图的黑色数据和蓝色数据各个较为集中,且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了,当然在实际应用中,我们的数据是多个类别的,我们的原始数据一般也是超过二维的,投影后的也一般不是直线,而是一个低维的超平面。
数学基础知识
瑞利商$R(A,x)$定义:
\[R(A,x) = \frac{x^HAx}{x^Hx}\]其中$x$为非零向量,而$A$为$n \times n$的Hermitan矩阵(自共轭矩阵,满足共轭转置矩阵和自己相等的矩阵,即$A^H=A$,矩阵中每一个第i行第j列的元素 都与 第j行第i列的元素的共轭相等)如果矩阵A是实矩阵,则满足$A^T=A$的矩阵即为Hermitan矩阵。
性质:瑞利商最大值等于矩阵A最大的特征值,最小值等于矩阵A的最小特征值
\[\lambda_{min} \leqslant \frac{x^HAx}{x^Hx} \leqslant \lambda_{max}\]广义瑞利商$R(A,B,x)$定义:
\[R(A,x) = \frac{x^HAx}{x^HBx}\]其中 $x$ 为非零向量,而$A,B$为$n \times n$的Hermitan矩阵。$B$为正定矩阵。
最大值为矩阵 $B^{-\frac{1}{2}}AB^{\frac{-1}{2}} $的最大特征值,或者说矩阵$ B^{-1}A $的最大特征值,最小值是其最小特征值
两类LDA原理
假设数据集$ D={(x_1,y_1),(x_2,y_2),……,(x_m,y_m)} $其中任意$ x_i $为n维向量
第j类样本的均值向量:
\[\mu_j = \frac{1}{n_j}\sum x(j=0,1)\]第j类样本的协方差矩阵:
\[\Sigma_j = \sum (x-\mu_j)(x-\mu_j)^T (j=0,1)\]由于是两类数据,因此我们只需要将数据投影到一条直线上即可,假设投影直线是向量 $\omega$ ,则对任意一个样本$ x_i$ ,它在直线$ \omega $的投影为$ \omega^Tx_i $,对于我们的两个类别的中心点 $\mu_0,\mu_1$ ,在在直线$ \omega $的投影为 $\omega^T\mu_0 , \omega^T\mu_1$ 。
-
由于LDA需要让不同类别的数据的类别中心之间的距离尽可能的大,也就是我们要最大化$\space \space \space \space \space \space$ $\parallel \omega^T\mu_0−\omega^T\mu_1\parallel _2^2 $
-
同时我们希望同一种类别数据的投影点尽可能的接近,也就是要同类样本投影点的协方差 $\omega^T\Sigma_0\omega$ 和 $\omega^T\Sigma_1\omega $尽可能的小,即最小化 $\omega^T\Sigma_0\omega+\omega^T\Sigma_1\omega $。
综上所述,我们的优化目标为:
\[arg max J(\omega) = \frac{||\omega^T\mu_0-\omega^T\mu_1||_2^2}{\omega^T\Sigma_0\omega+\omega^T\Sigma_1\omega} = \frac{\omega^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega}{\omega^T(\Sigma_0+\Sigma_1)\omega}\]类内散度矩阵 $S_\omega$ 为:
\[S_\omega = \Sigma_0 + \Sigma_1 = \sum(x-\mu_0)(x-\mu_0)^T+ \sum(x-\mu_1)(x-\mu_1)^T\]类间散度矩阵 $S_b$ 为:
\[S_b = (\mu_0-\mu_1)(\mu_0-\mu_1)^T\]优化目标重新定义:
\[argmax J(\omega) = \frac{\omega^TS_b\omega}{\omega^TS_\omega\omega}\]这就是广义瑞利商,最大值就是 $S_\omega^{-1}S_b $的最大特征值
多类LDA原理
优化目标:
\[argmax J(\omega) = \frac{\prod \omega^TS_b\omega}{\prod \omega^TS_\omega\omega} = \prod \frac{\omega^TS_b\omega}{\omega^TS_\omega\omega}\]特征向量最多有k-1个
优点
- 在降维过程中可以使用类别的先验知识经验,而像PCA这样的无监督学习则无法使用类别先验知识。
- LDA在样本分类信息依赖均值而不是方差的时候,比PCA之类的算法较优。
缺点
- LDA不适合对非高斯分布样本进行降维,PCA也有这个问题。
- LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1,则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
- LDA在样本分类信息依赖方差而不是均值的时候,降维效果不好。
- LDA可能过度拟合数据。
LDA算法流程
输入:数据集$D={(x_1,y_1), (x_2,y_2), …,((x_m,y_m))}$,其中任意样本$x_i$为n维向量,$y_i \in {C_1,C_2,…,C_k}$,降维到的维度d。
因为LDA是监督学习,所以与PCA相比需要输入标签
0) 中心化数据
1) 计算每个类别的均值向量。
2) 计算类间散度矩阵$S_b$和计算类内散度矩阵$S_w$
3) 计算类内散度矩阵的逆与类间散度矩阵的乘积$S_w^{-1}S_b$,求解特征值和特征向量矩阵
4) 计算$S_w^{-1}S_b$的最大的k个特征值和对应的k个特征向量$(w_1,w_2,…w_d)$,得到投影矩阵$W$
5) 对样本集中的每一个样本特征$x_i$,转化为新的样本$z_i=W^Tx_i$
6) 得到输出样本集$D’={(z_1,y_1), (z_2,y_2), …,((z_m,y_m))}$
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def LDA(X, Y, n_components):
# 1) 计算每个类别的均值向量。
class_means = []
unique_classes = np.unique(Y)
for c in unique_classes:
X_c = X[Y == c]
class_means.append(np.mean(X_c, axis=0))
# 2) 计算类间散度矩阵$S_b$和计算类内散度矩阵$S_w$
# 计算类内散度矩阵
within_class_scatter_matrix = np.zeros((X.shape[1], X.shape[1]))
for c, mean in zip(unique_classes, class_means):
X_c = X[Y == c]
scatter_matrix = np.zeros((X.shape[1], X.shape[1]))
for row in X_c:
row, mean = row.reshape(X.shape[1], 1), mean.reshape(X.shape[1], 1)
scatter_matrix += (row - mean).dot((row - mean).T)
within_class_scatter_matrix += scatter_matrix
# 计算类间散度矩阵
overall_mean = np.mean(X, axis=0)
between_class_scatter_matrix = np.zeros((X.shape[1], X.shape[1]))
for c, mean in zip(unique_classes, class_means):
n = X[Y == c].shape[0]
mean = mean.reshape(X.shape[1], 1)
overall_mean = overall_mean.reshape(X.shape[1], 1)
between_class_scatter_matrix += n * (mean - overall_mean).dot((mean - overall_mean).T)
# 3) 计算类内散度矩阵的逆与类间散度矩阵的乘积$S_w^{-1}S_b$,求解特征值和特征向量矩阵
eigvalues, eigvectors = np.linalg.eigh(np.linalg.inv(within_class_scatter_matrix) @ between_class_scatter_matrix)
eigvectors = eigvectors[:, np.argsort(eigvalues)[::-1]]
# 4) 计算$S_w^{-1}S_b$的最大的k个特征值和对应的k个特征向量$(w_1,w_2,...w_d)$,得到投影矩阵$W$
components = eigvectors[:, :n_components]
# 将数据投影到新的空间中
X_lda = np.dot(X, components)
return X_lda, components.T
利用数据降维算法对输入数据进行降维
只用训练集数据来学习 PCA 和 LDA 算法中的投影矩阵,并分别将两个方法相应的前 8 个特征向量变换回原来图像的大小进行显示。
展示所有图像:
 写一个转换的函数:
写一个转换的函数:
1
2
3
4
5
6
7
8
9
10
def transformToRaw(components):
fig, axes = plt.subplots(2, 4, figsize=(12, 6))
for i in range(8):
ax = axes[i // 4, i % 4]
eigenvector = components[i].reshape(64, 64)
ax.imshow(eigenvector, cmap='gray')
ax.set_title(f'PCA Component {i + 1}')
ax.axis('off')
plt.tight_layout()
plt.show()
只用训练集数据来计算 PCA 和 LDA 算法中的投影矩阵,然后调用即可:
1
2
3
4
5
6
7
8
9
# 使用PCA学习投影矩阵
projected_data_pca, components_pca = PCA(train_data, n_components=8)
# 将特征向量变换回原始图像的大小并显示
transformToRaw(components_pca)
# 使用LDA学习投影矩阵
projected_data_lda, components_lda = LDA(train_data, train_label, n_components=8)
# 将特征向量变换回原始图像的大小并显示
transformToRaw(components_lda)
PCA:

LDA:
然后对训练和测试数据用 PCA 和 LDA 分别进行数据降维(使用所学习的投影矩阵)。最后对采取 reduced_dim=2,即降维到 2 维后的训练和测试数据进行可视化,展示降维的效果(例如用第一维做 x,第二维做 y,不同类别采用不同颜色绘制散点图,这里只表示三类的情况,报告中应该是 15 个类)
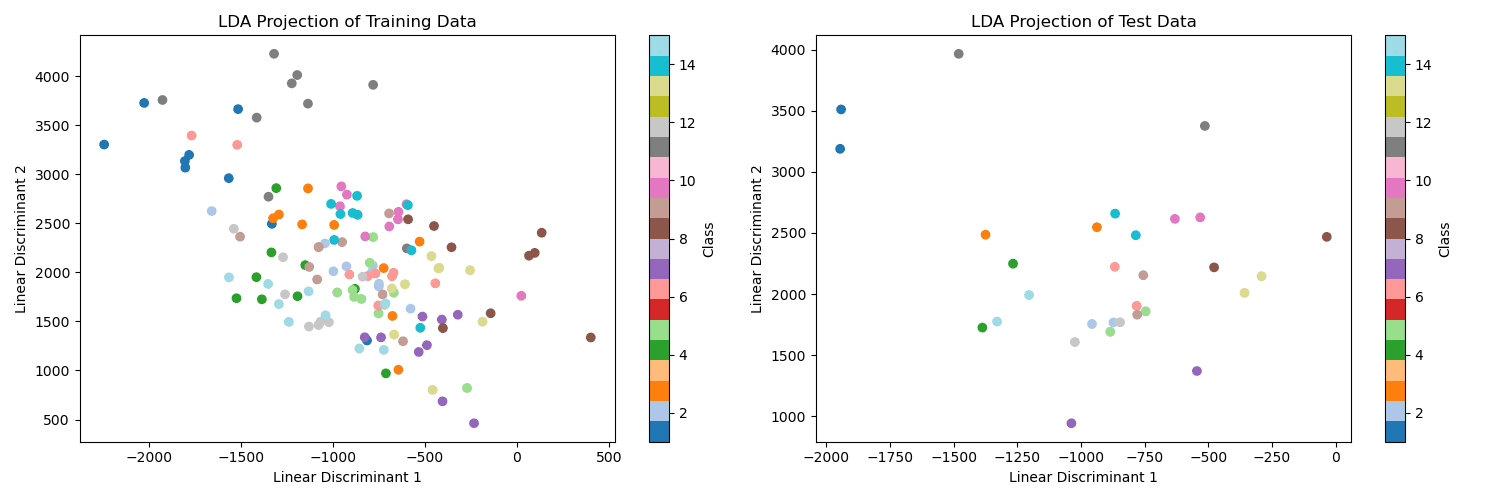
利用 KNN 算法进行训练和测试
利用降维后的训练数据作为 KNN 算法训练数据,降维后的测试数据作为评估 KNN 分类效果的测试集,分析在测试集上的准确率(压缩后的维度对准确率的影响,至少要给出压缩到 8 维的准确率)。
拓展:尝试利用不同的分类器,如 SVM 等达到更好的准确率。此部分允许调库。
介绍KNN
KNN,即K-Nearest Neighbors(K最近邻算法),是一种基于距离的监督学习算法,广泛应用于分类和回归问题。它的核心思想是:在特征空间中找到与目标点距离最近的K个点,根据这K个点的类别分布,来预测目标点的类别(分类问题),或者计算这K个点的属性值的平均值,来预测目标点的属性值(回归问题)。
KNN算法的特点:
- 简单直观:算法原理简单,容易理解和实现。
- 无需训练:KNN是一种惰性学习算法,它不需要在训练阶段建立模型,所有的计算都是在预测阶段进行。
- 对数据敏感:KNN对数据的分布非常敏感,因此对噪声和异常点比较敏感。
- 计算量大:在预测阶段需要计算目标点与训练集中每个点的距离,当训练集很大时,计算量会非常大。
- 存储空间大:需要存储全部数据集,对存储空间的需求较大。
- 维度灾难:当特征空间的维度很高时,KNN算法的性能会下降,可以通过降维技术来缓解这一问题。
KNN算法流程
- 距离度量:计算训练集中每个点与目标点之间的距离。常用的距离度量方法包括欧氏距离、曼哈顿距离等。
- 找到K个最近邻:根据距离度量结果,找出距离目标点最近的K个点。
- 决策规则(分类问题):
- 多数投票:统计这K个最近邻点中每个类别的数量,预测目标点属于数量最多的类别。
- 加权投票:根据距离的远近来加权,距离越近的点对预测结果的影响越大。
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def euclidean_distance(a, b):
"""计算两个点之间的欧几里得距离"""
return np.sqrt(np.sum((a - b) ** 2))
def knn_predict(X_train, y_train, X_test, k=3):
predictions = []
for x in X_test:
# 1.距离度量:计算未知样本与训练集中每个样本的距离
distances = [euclidean_distance(x, train_x) for train_x in X_train]
# 2.找出距离最近的K个邻居的索引
k_indices = np.argsort(distances)[:k]
# 获取这K个邻居的类别
k_nearest_labels = [y_train[i] for i in k_indices]
# 3.决策规则
# 统计邻居中每个类别的频率
label_counts = np.bincount(k_nearest_labels)
# 选择频率最高的类别作为未知样本的类别
most_common_label = np.argmax(label_counts)
predictions.append(most_common_label)
return predictions
结果
1
2
PCA压缩到8维的准确率: 0.9
LDA压缩到8维的准确率: 0.9333333333333333
调库使用KNN库的结果也是这样,说明KNN的实现没有问题,
进一步探索
同时使用其他的分类器,结果如下:
超参数选择默认,SVM的核函数选rbf
1
2
3
4
5
6
7
8
9
10
11
PCA压缩到8维的KNN准确率: 0.9
LDA压缩到8维的KNN准确率: 0.9333333333333333
PCA压缩到8维的SVM准确率: 0.7333333333333333
LDA压缩到8维的SVM准确率: 0.7666666666666667
PCA压缩到8维的决策树准确率: 0.6
LDA压缩到8维的决策树准确率: 0.6333333333333333
PCA压缩到8维的随机森林准确率: 0.8333333333333334
LDA压缩到8维的随机森林准确率: 0.8333333333333334
进一步,探索压缩到不同维度时的分类准确率
| 压缩技术 | 维度 | KNN准确率 | SVM准确率 | 决策树准确率 | 随机森林准确率 |
|---|---|---|---|---|---|
| PCA | 8 | 0.9 | 0.7333334 | 0.6 | 0.8333334 |
| LDA | 8 | 0.9333334 | 0.7666667 | 0.6333333 | 0.8333334 |
| PCA | 6 | 0.7666667 | 0.6666667 | 0.7333333 | 0.9 |
| LDA | 6 | 0.8 | 0.6666667 | 0.5666667 | 0.8 |
| PCA | 4 | 0.6333333 | 0.4 | 0.5333333 | 0.7666667 |
| LDA | 4 | 0.8 | 0.7333333 | 0.4333333 | 0.6666667 |
| PCA | 2 | 0.3 | 0.2 | 0.3333333 | 0.3 |
| LDA | 2 | 0.5 | 0.4 | 0.3666667 | 0.5 |
| PCA | 10 | 0.9333333 | 0.8 | 0.7666667 | 0.9 |
| LDA | 10 | 0.9333333 | 0.8 | 0.6666667 | 0.8666667 |
| PCA | 12 | 0.9333333 | 0.9 | 0.7 | 0.9666667 |
| LDA | 12 | 0.9666667 | 0.8333334 | 0.7 | 0.9666667 |
| PCA | 14 | 0.9333333 | 0.9 | 0.6666667 | 0.9666667 |
| LDA | 14 | 1.0 | 0.8333334 | 0.6666667 | 0.9333333 |
- KNN分类器的平均准确率为 0.8
- SVM分类器的平均准确率为 0.7
- 决策树分类器的平均准确率为 0.6222222
- 随机森林分类器的平均准确率为 0.8777778
不同维度平均准确率:
| 压缩技术 | KNN | SVM | 决策树 | 随机森林 |
|---|---|---|---|---|
| PCA | 0.77 | 0.64 | 0.58 | 0.84 |
| LDA | 0.86 | 0.73 | 0.55 | 0.81 |
综合分析:
- KNN:在PCA和LDA降维后,随着维度的增加,KNN的准确率先是提高,然后在较高维度时保持稳定。在LDA降维到14维时,准确率达到了1.0,这可能是由于LDA在降维时考虑了类别之间的判别信息,使得KNN能够在较低维空间中有效地进行分类。
- SVM:SVM在PCA降维后的性能不如LDA,特别是在低维空间中,SVM的准确率显著下降。这可能是因为PCA是一种无监督学习方法,不考虑类别信息,可能导致分类性能下降。然而,SVM在LDA降维后的性能有所提高,尤其是在较高维度时。
- 决策树:决策树在PCA和LDA降维后的性能都不如KNN和随机森林。随着维度的减少,决策树的准确率下降较快,这可能是因为决策树对特征的区分能力有限,需要更多的特征来辅助分类。
- 随机森林:随机森林在PCA和LDA降维后的性能都非常好,即使在低维空间中也能保持较高的准确率。这可能是因为随机森林作为一种集成学习算法,通过构建多个决策树并进行投票,提高了模型的泛化能力。
结论:
- 降维技术对分类器的性能有显著影响。PCA和LDA作为降维技术,它们对不同分类器的影响不同。LDA通常更适合分类问题,因为它考虑了类别之间的判别信息。
- 不同的分类器对降维后的特征空间敏感度不同,不是所有的分类器都适合在低维空间中工作。KNN和随机森林在较低维空间中仍然能够保持较好的分类性能,而SVM和决策树可能需要更多的特征维度来维持性能。
-
KNN和随机森林在较低维空间中表现较好,但也需要避免维度过低,以防丢失重要信息。
-
之后还尝试了更高维的数据,发现并不是保留维度越多分类越准确。
- 实验结果表明,降维并不是维度越低越好,需要根据具体算法和数据集特性来选择最合适的维度。
附录-前驱知识
特征值和特征向量
首先回顾下特征值和特征向量的定义如下:
\[Ax=\lambda x\]其中 A 是一个 $n\times n$ 矩阵, x 是一个 n 维向量,则 $\lambda $是矩阵 A 的一个特征值,而 x 是矩阵 A 的特征值$ \lambda $所对应的特征向量。
求出特征值和特征向量有什么好处呢? 就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的n个特征值$ \lambda_{1}\leq \lambda_{2}\leq… \leq \lambda_{n} $,以及这 n 个特征值所对应的特征向量 ${ w_{1},w_{2},…,w_{n} }$,
那么矩阵A就可以用下式的特征分解表示:
\[A=W\Sigma W^{-1}\]其中W是这n个特征向量所张成的n×n维矩阵,而$Σ$为这n个特征值为主对角线的n×n维矩阵。
一般我们会把W的这n个特征向量标准化,即满足$ \parallel w_{i} \parallel_{2}=1 $,或者$ w_{i}^{T}w_{i}=1$ ,此时W的n个特征向量为标准正交基,满足 $W^{T}W=I $,即 $W^{T}=W^{-1} $,也就是说W为酉矩阵。(酉矩阵是指其转置的共轭等于其逆,即$ 𝑊^𝑇=𝑊^{−1}$)
这样我们的特征分解表达式可以写成
\[A=W\Sigma W^{T}\]注意到要进行特征分解,矩阵A必须为方阵。
那么如果A不是方阵,即行和列不相同时,我们还可以对矩阵进行分解吗?答案是可以,此时就需要使用SVD了。
SVD的定义
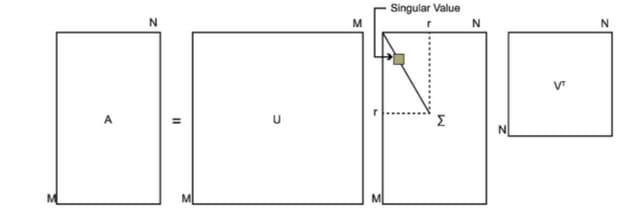
SVD也是对矩阵进行分解,但是和特征分解不同,SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵,那么我们定义矩阵A的SVD为:
\[A=U\Sigma V^{T}\]其中
- U 是一个$ m\times m$ 的矩阵
- $ \Sigma $是一个$ m\times n $的矩阵,除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值
- V 是一个$ n\times n$ 的矩阵。 U 和 V 都是酉矩阵,即满足$U^{T}U=I,V^{T}V=I $。
下图可以很形象的看出上面SVD的定义:
那么我们如何求出SVD分解后的U,Σ,V这三个矩阵呢?
如果我们将A的转置和A做矩阵乘法,那么会得到n×n的一个方阵 $A^{T}A $。既然$ A^{T}A $是方阵,那么我们就可以对$ A^{T}A $进行特征分解(将这个整体看为上一步的A),得到的特征值和特征向量满足下式:
\[(A^TA)v_i=\lambda_iv_i\]这样我们就可以得到矩阵 $A^{T}A $的n个特征值和对应的n个特征向量v了。将 $A^{T}A $的所有特征向量张成一个n×n的矩阵V,就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。
如果我们将A和A的转置做矩阵乘法,那么会得到m×m的一个方阵 $AA^{T}$ 。既然 $AA^{T} $是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
\[(AA^T)u_i = \lambda_iu_i\]这样我们就可以得到矩阵$ AA^{T}$ 的m个特征值和对应的m个特征向量u了。将$ AA^{T} $的所有特征向量张成一个m×m的矩阵U,就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。
U和V我们都求出来了,现在就剩下奇异值矩阵Σ没有求出了.
由于Σ除了对角线上是奇异值其他位置都是0,那我们只需要求出每个奇异值$σ$就可以了。
我们注意到:
\[A=U\Sigma V^T\Rightarrow AV=U\Sigma V^TV\Rightarrow AV=U\Sigma\Rightarrow Av_i=\sigma_iu_i\Rightarrow\sigma_i=Av_i/u_i\]这样我们可以求出我们的每个奇异值,进而求出奇异值矩阵$Σ$。
上面还有一个问题没有讲,就是我们说 $A^{T}A $的特征向量组成的就是我们SVD中的V矩阵,而
$AA^{T} $的特征向量组成的就是我们SVD中的U矩阵,这有什么根据吗?这个其实很容易证明,我们以V矩阵的证明为例。
\[A=U\Sigma V^T\Rightarrow A^T=V\Sigma U^T\Rightarrow A^TA=V\Sigma U^TU\Sigma V^T=V\Sigma^2V^T\]上式证明使用了 $U^{T}U=I,\Sigma^{T}\Sigma=\Sigma^2$ 。可以看出$ A^{T}A$ 的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到 $AA^{T}$ 的特征向量组成的就是我们SVD中的U矩阵。
进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足如下关系:
\[\sigma_{i}=\sqrt{\lambda_{i}}\]这样也就是说,我们可以不用 $\sigma_{i}=\frac{Av_{i}}{u_{i}} $来计算奇异值,也可以通过求出$ A^{T}A $的特征值取平方根来求奇异值。
tip:计算时不可以先算U V,再算中间矩阵,因为这样特征向量正负都无法确定,应该先算u或v再求中间矩阵推出v或u(奇异值分解(SVD)的评论区) 真正的U和V一定是$AA^T$和$A^TA$的特征向量组,但是直接求$AA^T$和$A^TA$的特征向量组不一定是U和V
理解:SVD是对数据进行有效特征整理的过程。首先,对于一个m×n矩阵A,我们可以理解为其有m个数据,n个特征,(想象成一个n个特征组成的坐标系中的m个点),然而一般情况下,这n个特征并不是正交的,也就是说这n个特征并不能归纳这个数据集的特征。SVD的作用就相当于是一个坐标系变换的过程,从一个不标准的n维坐标系,转换为一个标准的k维坐标系,并且使这个数据集中的点,到这个新坐标系的欧式距离为最小值(也就是这些点在这个新坐标系中的投影方差最大化),其实就是一个最小二乘的过程。进一步,如何使数据在新坐标系中的投影最大化呢,那么我们就需要让这个新坐标系中的基尽可能的不相关,我们可以用协方差来衡量这种相关性。$A^TA$中计算的便是n×n的协方差矩阵,每一个值代表着原来的n个特征之间的相关性。当对这个协方差矩阵进行特征分解之后,我们可以得到奇异值和右奇异矩阵,而这个右奇异矩阵则是一个新的坐标系,奇异值则对应这个新坐标系中每个基对于整体数据的影响大小,我们这时便可以提取奇异值最大的k个基,作为新的坐标,这便是PCA的原理。