
Pattern Recognition
HW1
Student ID: 21307381 Student Name: LJW
Date: 2024.4.30
Lectured by: Jinhua Ma
Pattern Recognition
Sun Yat-sen University
全景图拼接
实验目的
1、 熟悉 Harris 角点检测器的原理和基本使用
2、 熟悉 RANSAC 抽样一致方法的使用场景
3、 熟悉 HOG 描述子的基本原理
实验要求
1、 提交实验报告,要求有适当步骤说明和结果分析,对比
2、 将代码和结果打包提交
3、 实验可以使用现有的特征描述子实现
实验内容
1、使用 Harris 焦点检测器寻找关键点。
2、构建描述算子来描述图中的每个关键点,比较两幅图像的两组描述子,并进行匹配。
3、根据一组匹配关键点,使用 RANSAC 进行仿射变换矩阵的计算。
4、将第二幅图变换过来并覆盖在第一幅图上,拼接形成一个全景图像。
5、实现不同的描述子,并得到不同的拼接结果。
实验过程
Harris 角点算法
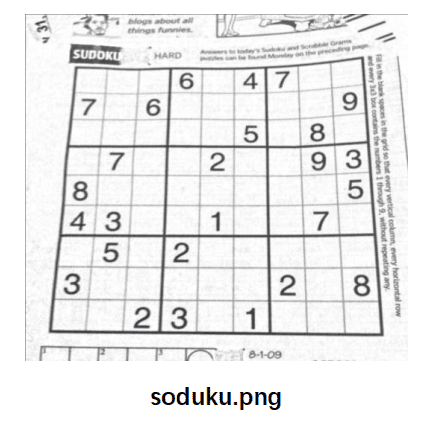
请实现 Harris 角点检测算法,并简单阐述相关原理,对 images/目录下的 sudoku.png 图像进行角点检测(适当进行后处理),输出对应的角点检测结果,保存到 results/目录下,命名为 sudoku_keypoints.png。
关键点描述与匹配
请使用实现的 Harris 角点检测算法提取 images/uttower1.jpg 和 images/uttower2.jpg 的关键点,并将提取的关键点检测结果保存到 results/目录下,命名为 uttower1_keypoints.jpg和 uttower2_keypoints.jpg。

分别使用 SIFT 特征和 HOG 特征作为描述子获得两幅图像的关键点的特征,使用欧几里得距离作为特征之间相似度的度量,并绘制两幅图像之间的关键点匹配的情况,将匹配结果保存到 results/目录下,命名为 uttower_match.png。
使用 RANSAC 求解仿射变换矩阵,实现图像的拼接,并将最后拼接的结果保存到 results/目录下,命名为 uttower_stitching_sift.png和 uttower_stitching_hog.png。并分析对比 SIFT 特征和 HOG 特征在关键点匹配过程中的差异。
请将基于 SIFT + RANSAC 的拼接方法用到多张图像上,对 images/yosemite1.png, images/yosemite2.png, images/yosemite3.png,images/yosemite4.png 进行拼接,并将结果保存到 results/目录下,命名为 yosemite_stitching.png。
拓展: HOG 相关内容参考: https://blog.csdn.net/hujingshuang/article/details/47337707
我的实验过程
Harris 角点算法
算法介绍
在现实世界中,角点对应于物体的拐角,道路的十字路口、丁字路口等。从图像分析的角度来定义角点可以有以下两种定义:
- 角点可以是两个边缘的角点;
- 角点是邻域内具有两个主方向的特征点;
Harris 角点算法是基于图像灰度的方法通过计算点的曲率及梯度来检测角点。
Harris Corner Detector:如果以一个角点为中心构造一个区域,那么这个区域朝任何一个方向移动都会有较大的灰度值变化。如下图所示
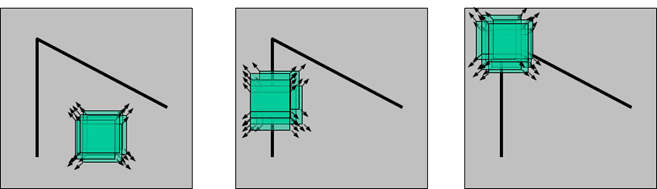
人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。
- 左图:如果这个特定的窗口在图像各个方向上移动时,窗口内图像的灰度没有发生变化,那么窗口内就不存在角点;
- 中间图:如果窗口在某一个方向移动时,窗口内图像的灰度发生了较大的变化,而在另一些方向上没有发生变化,那么,窗口内的图像可能就是一条直线的线段。
- 右图:如果在各个方向上移动这个特征的小窗口,窗口内区域的灰度发生了较大的变化,那么就认为在窗口内遇到了角点。
对于图像$I(x,y)$,当在点$(x,y)$处平移$(\Delta x,\Delta y)$后的自相似性,可以通过自相关函数给出:
\[c(x,y;\Delta x,\Delta y) = \sum_{(u,v)\in W(x,y)}w(u,v)(I(u,v) – I(u+\Delta x,v+\Delta y))^2\]其中,$W(x,y)$是以点$(x,y)$为中心的窗口,$w(u,v)$为加权函数(这里的权重w考虑到不同像素点的贡献不同),它既可是常数,也可以是高斯加权函数。下面取为常数1

如果领域中心为角点,则无论$u,v$取何值,$c$都具有较大的值。这里我们使用多变量函数的泰勒展开,对图像$I(x,y)$在平移$(\Delta x,\Delta y)$后进行一阶近似:
\[I(u+\Delta x,v+\Delta y) = I(u,v)+I_x(u,v)\Delta x+I_y(u,v)\Delta y+O(\Delta x^2,\Delta y^2)\\ \approx I(u,v)+I_x(u,v)\Delta x+I_y(u,v)\Delta y\]其中,$I_x,I_y$是图像$I(x,y)$的偏导数,这样的话,自相关函数则可以简化为(将(2)带回(1)消去$I(u,v)$):
\[c(x,y;\Delta x,\Delta y)\approx \sum_w w(u,v)(I_x(u,v)\Delta x+I_y(u,v)\Delta y)^2\\ =\sum_w w(u,v)(\Delta x^2I_x^2+2\Delta x\Delta yI_xI_y+\Delta y^2I_y^2)^2\\ =\sum_w w(u,v)\begin{bmatrix}\Delta x&\Delta y\end{bmatrix}\quad\begin{bmatrix}\mathrm{I_x^2}&&\mathrm{I_{x}I_{y}}\\\mathrm{I_{x}I_{y}}&&\mathrm{I_y^2}\end{bmatrix}\quad\begin{bmatrix}\Delta x\\\Delta y\end{bmatrix} \\ =\begin{bmatrix}\Delta x&\Delta y\end{bmatrix}(\space \sum_w w(u,v)\quad\begin{bmatrix}\mathrm{I_x^2}&&\mathrm{I_{x}I_{y}}\\\mathrm{I_{x}I_{y}}&&\mathrm{I_y^2}\end{bmatrix}\quad)\begin{bmatrix}\Delta x\\\Delta y\end{bmatrix} \\ [\Delta x,\Delta y]M(x,y)\begin{bmatrix}\Delta x \\ \Delta y\end{bmatrix}\]其中
\[M(x,y)=\sum_w w(u,v)\quad \begin{bmatrix}I_x(x,y)^2&I_x(x,y)I_y(x,y) \\ I_x(x,y)I_y(x,y)&I_y(x,y)^2\end{bmatrix} \\ = \begin{bmatrix}\sum_w I_x(x,y)^2&\sum_w I_x(x,y)I_y(x,y) \\\sum_w I_x(x,y)I_y(x,y)&\sum_w I_y(x,y)^2\end{bmatrix} =\begin{bmatrix}A&C\\C&B\end{bmatrix}\]由于M为实对称矩阵,所以可以写成如下形式:
\[\mathrm{M}=\mathrm{P} \Sigma\mathrm{P}^{-1}=\mathrm{P} \Sigma\mathrm{P}^\mathrm{T}\]其中
\[Σ=\begin{bmatrix}\lambda_1&0\\0&\lambda_2\end{bmatrix}\]为特征值矩阵,$P$ 为特征值对应特征向量矩阵。所以
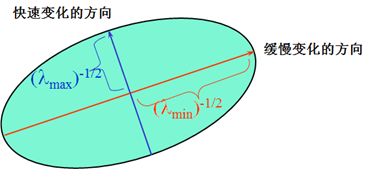
\[\begin{aligned}c(x,y;\Delta x,\Delta y)&=\begin{bmatrix}\Delta x&\Delta y\end{bmatrix}\mathrm{P}\begin{bmatrix}\lambda_1&0\\0&\lambda_2\end{bmatrix}\mathrm{P}^\mathrm{T}\begin{bmatrix}\Delta x&\Delta y\end{bmatrix}^\mathrm{T}\\ &=\begin{bmatrix}\Delta x^,&\Delta y^,\end{bmatrix}\begin{bmatrix}\lambda_1&0\\0&\lambda_2\end{bmatrix}\begin{bmatrix}\Delta x^,&\Delta y^,\end{bmatrix}^\mathrm{T}\\ &=\frac{(\Delta x^,)^2}{\frac1{\lambda_1}}+\frac{(\Delta y^,)^2}{\frac1{\lambda_2}}\end{aligned}\]也就是一个椭圆方程形式,椭圆的扁率和尺寸是由$M(x,y)$的特征值$\lambda_1、\lambda_2$决定的,椭贺的方向是由$M(x,y)$的特征矢量决定的,如下图所示,椭圆方程为:
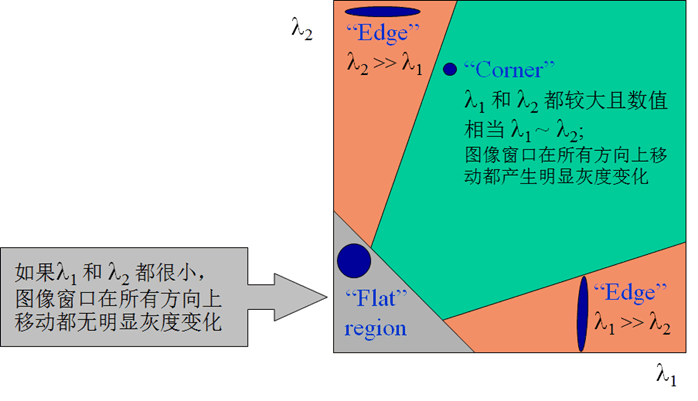
椭圆函数特征值与图像中的角点、直线(边缘)和平面之间的关系如下图所示。共可分为三种情况:
- 图像中的直线。一个特征值大,另一个特征值小,𝜆1≫𝜆2或𝜆2≫𝜆1。自相关函数值在某一方向上大,在其他方向上小。
- 图像中的平面。两个特征值都小,且近似相等;自相关函数数值在各个方向上都小。
- 图像中的角点。两个特征值都大,且近似相等,自相关函数在所有方向都增大。
所以当 $\lambda_1$ 和 $\lambda_2$ 都很大时,$c(x,y;\Delta x,\Delta y)$ 也会很大。由于 $detM = \lambda_1 \lambda_2=AC−B^2$ ,$tranceM=\lambda_1+ \lambda_2=A+C$,所以可以构造变量$R=detM-k(tranceM)^2$。$R$越大为角点的可能性越大,$k$为经常常数,一般取0.04~0.06。
实现步骤
1) RGB 彩色图片转成灰度图
2) 使用 Sobel 等梯度算子计算每一个点 x, y 两个方向上的梯度 $I_{x}, I_{y}$
3) 为构建 M 矩阵做准备,${I_{x}}^2, {I_{y}}^2$和${I_{x}}{I_{y}}$
4) 对$ {I_{x}}^2, {I_{y}}^2 $和$ {I_{x}}{I_{y}} $做局部窗口的高斯滤波(或均值滤波)
卷积可以对图像中的梯度信息进行平滑处理,以降低噪声的影响并使角点检测结果更稳定。通过对图像的梯度信息与一个窗口进行卷积,可以得到每个像素点周围区域的梯度信息的加权平均值。这样做可以使角点检测更加准确,并且增强角点的局部特征,有助于提高检测的稳定性和鲁棒性。
5) 对图像中的每一个点,构建
\[M = \sum_{x,y} w(x,y) \begin{bmatrix} I_{x}^2 & I_{x}I_{y} \\ I_{x}I_{y} & I_{y}^2 \end{bmatrix} = \begin{bmatrix} A & C\\ C & B \end{bmatrix}\]6) 求 $det(M) - k \cdot trace(M)^2 $,参数$ k$ 一般取 0.04 - 0.06,响应值大于一定阈值的点保存,作为角点。
7) 每个角点,统计局部特征,做后续的图像匹配等。
下面是伪代码,具体代码见my_harris.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 1. 读取灰度图像
gray_image = 读取灰度图像函数('your_image.jpg')
# 2. 计算图像梯度
dx = 计算水平方向梯度函数(gray_image)
dy = 计算垂直方向梯度函数(gray_image)
# 3. 计算协方差矩阵
window_size = 3
k = 0.04
corner_response = 初始化角点响应矩阵为零(gray_image.shape)
for each pixel in gray_image:
在窗口内计算dx*dx, dy*dy, dx*dy
计算协方差矩阵M
计算角点响应R = det(M) - k * trace(M)^2
存储R到corner_response中
# 4. 非极大值抑制
for each pixel in corner_response:
在周围区域内比较角点响应值,保留局部最大值
# 5. 阈值处理
threshold = 设定阈值
for each pixel in corner_response:
如果角点响应值大于阈值,标记为角点
# 6. 显示结果
显示带有角点标记的图像
实验结果
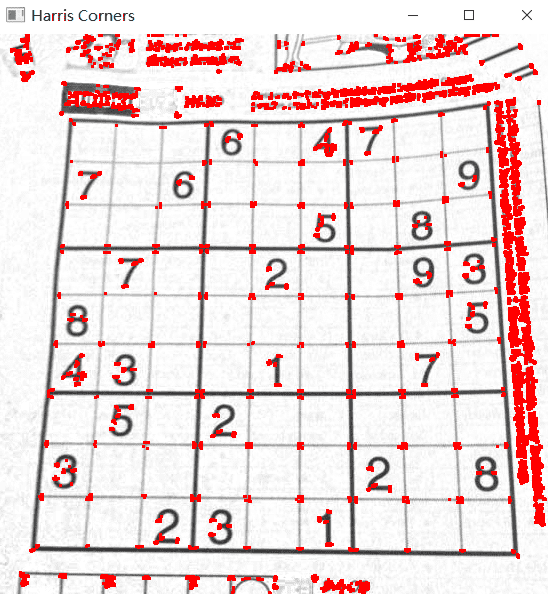
调库dst = cv2.cornerHarris(gray, 2, 3, 0.04):
我的实现:
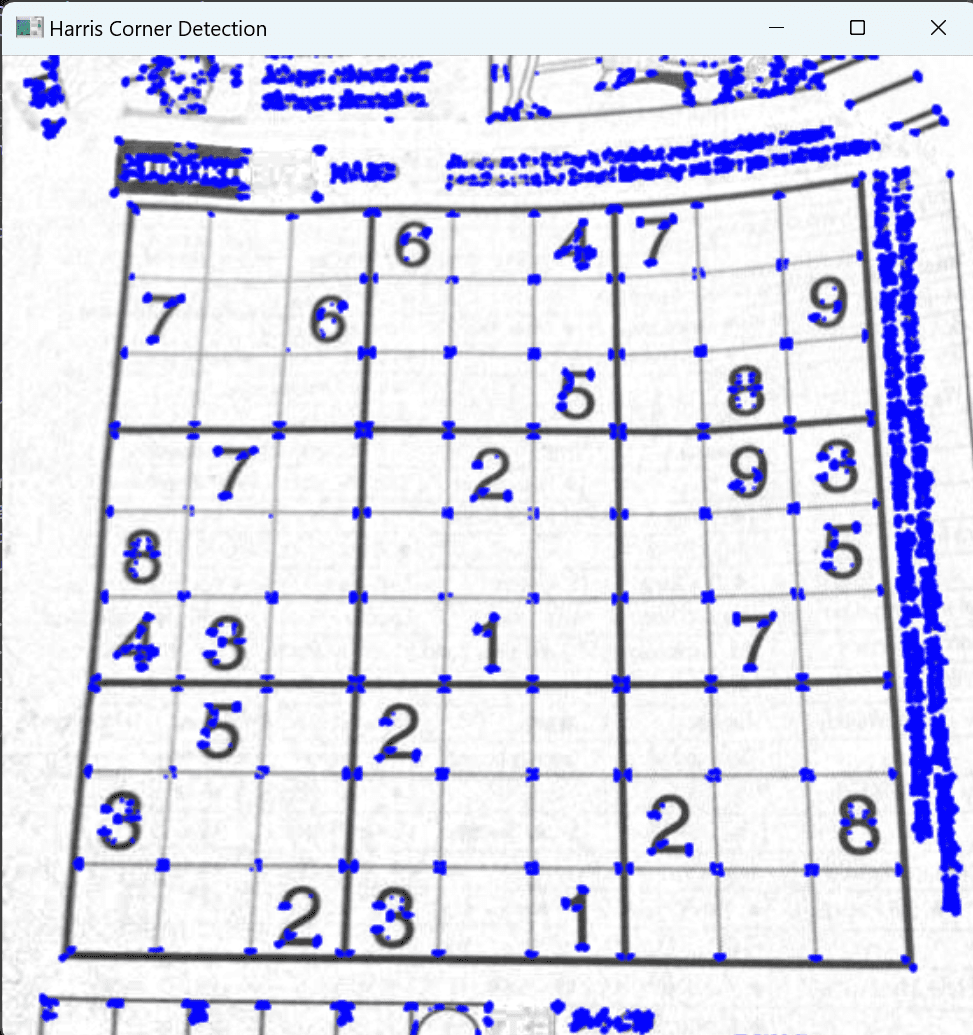
可以看到我实现的harris可以成功的找到角点的位置,且与库函数找到的基本一致,说明实现成功。
关键点描述与匹配
要求一:
首先使用实现的 Harris 角点检测算法提取
images/uttower1.jpg和images/uttower2.jpg的关键点,并将提取的关键点检测结果保存到 results/目录下,命名为uttower1_keypoints.jpg和uttower2_keypoints.jpg。
直接调用已经实现的函数即可:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from my_harris import harris_corners
import cv2
if __name__ == '__main__':
# 读取彩色图像
image1 = cv2.imread('images/uttower1.jpg')
image2 = cv2.imread('images/uttower2.jpg')
# 检测角点并在彩色图像上显示
keypoints1 = harris_corners(image1)
keypoints2 = harris_corners(image2)
# 在彩色图像上标记角点
image_with_corners1 = cv2.drawKeypoints(image1, keypoints1, None, color=(0, 0, 255),
flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
image_with_corners2 = cv2.drawKeypoints(image2, keypoints2, None, color=(0, 0, 255),
flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
# 显示结果
cv2.imwrite('results/uttower1_keypoints.jpg', image_with_corners1)
cv2.imwrite('results/uttower2_keypoints.jpg', image_with_corners2)
结果如下图


要求二
分别使用 SIFT 特征和 HOG 特征作为描述子获得两幅图像的关键点的特征,使用欧几里得距离作为特征之间相似度的度量,并绘制两幅图像之间的关键点匹配的情况,将匹配结果保存到 results/目录下,命名为 uttower_match.png。
下面我们以两张图片检测到的关键点为中心构建一个区域计算描述子,然后遍历图片1每一个关键点,计算其与图片2每一个关键点的欧氏距离,如果最小距离与次小距离的比值小于某个阈值,则认为最小距离对应的图1关键点和图2关键点匹配。
以下是我实现的匹配函数:首先创建了一个暴力匹配器(Brute Force Matcher)对象bf,它使用L2范数(即欧几里得距离)来比较描述符之间的距离。然后使用bf对象对两个图像的描述符进行最近邻(k-nearest neighbors,knn)匹配,k=2意味着为每个描述符找到两个最近邻。之后对于每个匹配对,计算较好匹配和次好匹配的距离比。如果这个比值小于0.4,认为成功匹配。
1
2
3
4
5
6
7
8
9
def match(descriptors1, descriptors2, image1, image2, keypoints1, keypoints2):
bf = cv2.BFMatcher(cv2.NORM_L2)
matches = bf.knnMatch(descriptors1, descriptors2, k=2)
good_matches = []
for m, n in matches:
if m.distance / n.distance < 0.4 :
good_matches.append(m)
match_img = cv2.drawMatches(image1, keypoints1, image2, keypoints2, good_matches, None, flags=cv2.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS)
return match_img, good_matches
HOG
HOG(Histogram of Oriented Gridients的简写)特征检测算法
这里我实现了自己的HOG算法,具体见function.py,简单来说HOG特征检测算法包含以下几个步骤:
一、图像预处理
- 图像裁剪和缩放:将图像裁剪为等大小的单元格cell,并缩放到固定尺寸。
- (可选)梯度计算:对于彩色图像,计算每个像素点的梯度,选取最大梯度作为该像素的梯度。
- 伽马矫正:调整图像对比度,减少光照对图像的影响,以确保图像正常化。伽马矫正公式为$f(x)=x^{\gamma}$,其中$\gamma$越大,图像越暗。
二、计算梯度图 利用Sobel核与图像卷积,分别求得$x$和$y$方向的梯度图,进而得到总的梯度图和梯度方向图。
三、计算梯度直方图 将整个图像划分为若干个8×8的小单元格,称为cell(还可是16×16或者32×32,是可调参数)。由于每个每个像素对应着一个梯度幅值和梯度方向,所以一个cell包含8×8×2=128个值。然后,将180度的角度范围分为9份,每20度为一个bin,并将梯度幅值按照比例分配到对应的bin中。
四、Block归一化 以8×8的cell为基本单元,形成2×2的block,每个block包含36个值。通过滑动窗口的方式对每个block进行归一化处理。
五、特征向量维度 对于64×128像素的图片,经过处理后的特征向量维度为3780,即由8×16个cell、7×15个block和每个block的36个值组成。
运行效果:

不难发现匹配的还是很精确的。
SIFT
SIFT算法又叫尺度不变特征变换匹配算法
SIFT(Scale-Invariant Feature Transform)是一种用于检测和描述图像局部特征的经典算法,其基本思想是通过检测图像中的关键点,并对这些关键点进行描述,从而实现图像的特征匹配和识别。以下是SIFT算法的基本步骤:
-
尺度空间极值检测: SIFT算法首先在不同的尺度下对图像进行平滑处理,并在每个尺度空间中检测图像的极值点(关键点),这些点通常对于图像的局部结构具有显著的特征。
-
关键点定位: 在检测到的极值点的基础上,通过对图像局部区域进行边缘响应值的计算,排除低对比度的关键点以及具有较弱梯度的边缘点,从而确定最终的关键点位置。
这里我们先用了harris找到了关键点,所以其实我们只是用到了后面几步
-
关键点方向分配: 对于每个关键点,SIFT算法计算其主方向或梯度方向,以确保关键点对于旋转具有不变性。通常采用图像梯度方向的直方图来确定主方向。
-
关键点描述: 在确定了关键点的位置和方向后,SIFT算法以关键点为中心,在其周围区域内构建描述子,通常使用局部图像梯度的方向和幅度信息来描述关键点周围的局部特征。
-
特征向量匹配: 最后,通过比较不同图像中的关键点描述子,使用一种距离度量方法(如欧式距离或汉明距离)来计算它们之间的相似性,并进行特征向量的匹配,从而实现图像的特征检测、配准和匹配。
SIFT的实现太复杂了,查看了一下网上实现了的代码,需要400行(见pysift.py),而且效率不如调库的1/10,所以这一个算法我选择直接调库。

要求三
使用 RANSAC 求解仿射变换矩阵,实现图像的拼接,并将最后拼接的结果保存到 results/目录下,命名为 uttower_stitching_sift.png和 uttower_stitching_hog.png。并分析对比 SIFT 特征和 HOG 特征在关键点匹配过程中的差异。
RANSAC(Random Sample Consensus)是一种经典的模型参数估计方法,常用于解决数据中存在噪声和异常值的情况下的模型拟合问题。其基本步骤如下:
- 随机选取样本集: 首先从数据集中随机选择一小部分样本作为候选集合,这些样本将用于拟合模型。
- 模型拟合: 使用所选样本集合的这些点来计算仿射变换矩阵。
- 验证模型: 对于其他数据点,计算它们到模型的拟合误差,并根据预先设定的阈值确定哪些点被认为是内点(即与模型拟合良好的点)。
- 迭代过程: 不断重复上述过程,每次都选择具有最大内点数目的模型,直到达到预定的迭代次数或者内点数目满足某个预设的阈值。
- 模型优化: 在最终迭代完成后,利用所有被认定为内点的数据重新拟合模型,以得到更精确的参数估计。在这种情况下,对保留的最大内点进行最小二乘法的估计,得到图像的仿射变换矩阵。
RANSAC 的一个优点是它能够对模型参数进行鲁棒估计,能够在存在大量噪声的情况下找到合适的模
RANSAC 的缺点是计算这些参数所需的时间没有上限,其需要进行大量的随机采样和模型拟合,因此对于大规模数据集来说,计算复杂度较高,可能需要较长的时间来运行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def transform(keypoints1, keypoints2, good_matches, image1, image2, match_img):
aim_points = np.float32([keypoints1[m.queryIdx].pt for m in good_matches]).reshape(-1, 1, 2)
src_points = np.float32([keypoints2[m.trainIdx].pt for m in good_matches]).reshape(-1, 1, 2)
# 使用RANSAC算法估计仿射变换矩阵
transform_matrix, mask = cv2.findHomography(src_points, aim_points, cv2.RANSAC)
# 扩充原图,以保障仿射变换和拼接后图片不会被裁剪
height, width = image1.shape[:2]
result_height = int(height * 1.1)
result_width = int(width * 1.6)
image1 = cv2.copyMakeBorder(image1, 0, result_height - height, 0, result_width - width, cv2.BORDER_CONSTANT, value=(0, 0, 0))
image2 = cv2.copyMakeBorder(image2, 0, result_height - height, 0, result_width - width, cv2.BORDER_CONSTANT, value=(0, 0, 0))
# 转换第二张图到第一张图的视角
rows, cols = image2.shape[:2]
transform_image = cv2.warpPerspective(image2, transform_matrix, (cols, rows))
# 调整图像尺寸,使其具有相同的尺寸
rows1, cols1 = image1.shape[:2]
rows2, cols2 = transform_image.shape[:2]
# 确定新的目标尺寸
final_rows = max(rows1, rows2)
final_cols = max(cols1, cols2)
# 调整图像大小
image1_resized = cv2.resize(image1, (final_cols, final_rows))
image2_aligned_resized = cv2.resize(transform_image, (final_cols, final_rows))
# 拼接在一起,以第一张图为主
result = np.where(image1_resized != 0, image1_resized, image2_aligned_resized)
return result
结果:左边为hog的结果,右边为sift的结果,可以看到hog的图二是更加歪的,导致顶端出有一个很小的黑色三角。
两个最明显的区别就是sift比hog运行速度快很多。
特征描述方式的区别:
- SIFT特征:SIFT描述子是基于局部图像梯度的方向和幅度信息构建的,通常是一个128维的向量,每个维度代表了关键点周围局部区域的特征信息。
- HOG特征:HOG描述子是基于图像梯度的直方图构建的,主要用于描述图像局部区域的纹理和形状信息,通常是一个高维的向量。
尺度和旋转不变性:
- SIFT特征:SIFT在检测关键点时考虑了尺度空间,在描述关键点时也考虑了其主方向,因此具有一定的尺度和旋转不变性。
- HOG特征:HOG主要用于描述局部图像的纹理和形状信息,在尺度和旋转变化较大时可能不太稳定。
- 从要求三的图片中也可以看到sift找到的匹配点要比hog多一点。


要求四
请将基于 SIFT + RANSAC 的拼接方法用到多张图像上,对 images/yosemite1.png, images/yosemite2.png, images/yosemite3.png,images/yosemite4.png 进行拼接,并将结果保存到 results/目录下,命名为 yosemite_stitching.png。
这里直接调之前写好的match和transforml两个函数即可,但是这里有多种调用顺序:
- 先拼12,34,然后将两个的结果再次拼在一起
- 先拼12,12结果与3拼,123结果再与4拼
- 23先拼,然后和14拼在一起
这里我实现了第一和第二种,结果如下
先拼12,34,然后将两个的结果再次拼在一起结果:

先拼12,12结果与3拼,123结果再与4拼结果:

可以发现一个问题:先拼接后的图像与其他图像拼接时接缝处会有一条黑边,分析:
-
图像拉伸导致的形变: 图像在拼接过程中可能会经过拉伸或缩放以适应其他图像的尺寸,可能会导致图像的局部区域发生形变。这种形变可能会影响图像中的关键点,因为关键点通常是基于图像的局部特征来检测的,形变会改变这些局部特征,从而影响关键点的准确性。
-
关键点检测的不稳定性: 由于形变的存在,关键点检测算法可能无法在拼接后的图像中稳定地检测到与原图像相同的关键点。这种不稳定性可能会导致后续的特征匹配和变换矩阵计算出现问题。
-
变换矩阵的计算误差: 在图像拼接中,变换矩阵用于将一个图像中的点映射到另一个图像的坐标空间中。如果关键点检测不准确,那么计算出的变换矩阵可能包含误差,这将导致拼接后的图像与原图像之间出现不匹配的接缝。
-
图像边界处理: 当图像边缘处的特征点较少或者边缘特征不明显时,拼接算法可能无法有效地处理这些区域。这可能导致在拼接边界处出现黑色或不自然的边缘。
参考文档
图像处理基础(七)Harris 角点检测 - 知乎 (zhihu.com)
【特征检测】HOG特征算法_比较两幅图像相似性-基于hog特征-CSDN博客