中山大学机器学习与数据挖掘期末复习笔记
Lec 00 Intro
- 什么是机器学习?
- PTE 模型:机器学习是研究在经验为 E 的情况下,提高其在任务 T 上的性能 P 的算法。
- 机器学习的泛化能力:模型、算法对新鲜样本的适应能力。
- 什么是数据挖掘?
- 给定大量的数据来发现有效、可用、意料之外的、可理解的模式和模型。
- 对比机器学习和数据挖掘
- 机器学习实践者使用数据作为训练集,来训练算法;数据挖掘使用算法从数据中发现有趣的模式。
Lec 01 线性回归
1. 是回归问题?
- 根据给定的特征,预测感兴趣变量的值。
- 数学表示:$\hat{y} = f(x_1, x_2,…x_m)$
2. 线性回归的数学表示
\[f(x_1, x_2, \dots, x_m) = w_0 + w_1x_1 + w_2x_2 + ... + w_mx_m\]3. 线性回归的损失函数(均方误差 MSE)
\[L(w) = \frac1n\sum_{i=1}^n(f(x^{(i)}) - y^{(i)})^2\]4. 单变量线性回归的损失函数构建与最优解
\[L(w_0, w_1) = \frac1n\sum_{i=1}^n(w_0 + w_1x^{(i)} - y^{(i)})^2\]算偏导,偏导为零时取得最优解
\[w=\frac{\partial L}{\partial w_0} = 0,\frac{\partial L}{\partial w_1} = 0\]最后结果:联立 $w_0, w_1$ 时容易算错,用均值 $\overline{a} = \sum a_i$ 表示更方便
\[w_0 = \frac{\overline{xy}\text{ }\overline{x} - \overline{x^2}\overline{y}}{\overline{x}^2 - \overline{x^2}}, w_1 = \frac{\overline{x}\text{ }\overline{y} - \overline{xy}}{\overline{x}^2 - \overline{x^2}}\]5. 多变量情况(一般情况)线性回归的损失函数构建与最优解(引入对向量及向量求导)
\[f(\mathbf{x}) = \mathbf{x}\mathbf{w} \\ \mathbf{x} = [1, x_1, x_2, ..., x_m] \in \mathbb{R}^{1\times(m+1)} \\ \mathbf{w} = [w_0, w_1, w_2, ..., w_m]^\mathbf{T} \in \mathbb{R}^{(m +1)\times1}\]损失函数可以写成:
\[L(\mathbf{w}) = \frac1n\sum_{i = 1}^n(\mathbf{x}^{(i)}\mathbf{w}-y^{(i)})^2 \\ L(\mathbf{w}) = \frac1n ||\mathbf{X}\mathbf{w}-\mathbf{y}||^2 \\ \mathbf{X} = [x^{(1)^\mathbf{T}}, x^{(2)^\mathbf{T}}, ..., x^{(n)^\mathbf{T}}]^\mathbf{T} \in \mathbb{R}^{n \times(m + 1)} \\ \mathbf{y} = [y^{(1)}, y^{(2), ..., y^{(n)}}] \in \mathbb{R}^{n\times 1}\]6. 常用的推导规则:(注意看分子是标量还是向量)
标量对向量求导:分子标量,分母向量,结果与分母一个形状
\[||\mathbf x||^2 = \mathbf x^T\mathbf x \\ \frac{\partial \mathbf a^T\mathbf x}{\partial \mathbf x} = \frac{\partial\mathbf x^T \mathbf a}{\partial \mathbf x} = \mathbf a \\ \frac{\partial \mathbf x^T\mathbf x}{\partial \mathbf x} = 2\mathbf x\\ \frac{\partial \mathbf x^T \mathbf A \mathbf x}{\partial \mathbf x} = (\mathbf A + \mathbf A^T)\mathbf x \\ \frac{\partial z}{\partial \mathbf x} = (\frac{\partial \mathbf y}{\partial \mathbf x})^T\frac{\partial z}{\partial \mathbf{y}} \text{ 链式法则 } \mathbf x \to \mathbf y \to z\]向量对向量求导:分子向量,分母向量,结果往往是矩阵(?)
\[\frac{\partial \mathbf A\mathbf x}{\partial \mathbf x} = \mathbf A \\ \frac{\partial\mathbf x^T \mathbf A}{\partial \mathbf x} = \mathbf A^T \\ \frac{\partial \mathbf z}{\partial \mathbf x} = \frac{\partial \mathbf z}{\partial \mathbf y}\frac{\partial \mathbf y}{\partial \mathbf x} \text{ 链式法则 } \mathbf x \to \mathbf y \to \mathbf z\]标量对矩阵求导:分子标量,分母矩阵
\[\frac{\partial \mathbf a^T\mathbf X \mathbf b}{\partial \mathbf X} = \mathbf a\mathbf b^T \\ \frac{\partial z}{\partial \mathbf X} = \mathbf A^T \frac{\partial z}{\partial \mathbf Y} \text{ 链式法则 } z = f(\mathbf Y), \mathbf Y = \mathbf A \mathbf X + \mathbf B\]算偏导:
\[\frac{\partial{L(\mathbf{w})}}{\partial\mathbf{w}} = \frac2n\mathbf{X}^T(\mathbf{X}\mathbf{w}-\mathbf{y}) = 0 \\ \mathbf{w}^* = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}\]7. 梯度下降
\[\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - r \cdot \frac{\partial L(\mathbf{w})}{\partial \mathbf{w}}|_{w = w^{(t)}} = \mathbf{w}^{(t)} - r \cdot\frac1n\sum_{i = 1}^n\frac{\partial l(\mathbf{w}, \mathbf{x}^{(i)}, y^{(i)})}{\partial{\mathbf{w}}}\]8. 随机梯度下降:将样本分为若干 Batch
\[\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - r \cdot\frac1{|B_t|}\sum_{i \in B_t}\frac{\partial l(\mathbf{w}, \mathbf{x}^{(i)}, y^{(i)})}{\partial{\mathbf{w}}}\]Lec 02 线性分类器
1. 二分类问题(逻辑回归与 Sigmoid 函数)
- Sigmoid 函数:$ \sigma(x) = \frac{1}{1 + e^{-x}} $:
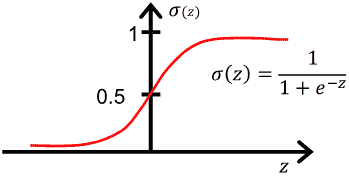
-
逻辑回归问题:$f(\mathbf x) = \sigma(\mathbf x\mathbf w)$,就是在线性回归的基础上套一个 Sigmoid 函数
-
平方误差损失函数:$L(\mathbf w) = (\sigma(\mathbf x\mathbf w) - y)^2, y \in {0, 1}$
- 交叉熵损失函数:
- \[L(\mathbf w) = -y\log(\sigma(\mathbf x\mathbf w)) - (1 - y) \log(1 - \sigma( \mathbf x\mathbf w))\]
交叉熵函数曲线是凸函数,而平方误差函数曲线非凸,凸函数更容易进行优化。
取对数:一个是为了防止下溢,一个是使得连乘变连加
- 判别边界:
2. 多分类问题(Softmax 函数)
-
基于二分类的 One vs All 方法:每次划分一个类,结果取 argmax
- Softmax 函数:
-
\[softmax_i(\mathbf z) = \frac{e^{z_i}}{\sum_{k = 1}^Ke^{z_k}}\]
数据 $\mathbf x$ 属于第 $i$ 类的概率:
$f_i(\mathbf x) = softmax_i(\mathbf x\mathbf W) = \frac{e^{\mathbf x \mathbf w_i}}{\sum_{k = 1}^Ke^{\mathbf x \mathbf w_k}}, \mathbf x \in \mathbb R^{1\times d}, \mathbf W = [\mathbf w_1, …, \mathbf w_k] \in \mathbb R^{d\times k} $
- Softmax 函数与 Sigmoid 函数的关系:当 $K = 2$ 时,有两类softmax分类等价于逻辑回归,参数为 $\mathbf w_1 - \mathbf w_2$
- \[softmax_1(\mathbf x\mathbf W) = \sigma(\mathbf x(\mathbf w_1 - \mathbf w_2)) \\ softmax_2(\mathbf x\mathbf W) = 1 - \sigma(\mathbf x(\mathbf w_1 - \mathbf w_2))\]
-
独热向量
- 交叉熵损失函数:
- \[L(\mathbf w_1, \mathbf w_2, ..., \mathbf w_K) = -\frac1n\sum_{i = 1}^n\sum_{k = 1}^K y_k^{(i)}\log softmax_k(\mathbf x ^{(i)}\mathbf W)\]
- 梯度下降:$\frac{\partial L(\mathbf W)}{\partial \mathbf W} = \frac1n\sum_{i = 1}^n(softmax(\mathbf x^{(i)}\mathbf W) - \mathbf y^{(i)})$
- Sigmoid 的导数:$\sigma’(x) = \sigma(x)(1 - \sigma(x))$
Lec 03 从概率角度理解回归和分类问题
- 从概率的角度来看,线性回归实际上等于
- 建模:假设条件分布为高斯分布
- 训练:通过最大化对数似然来训练模型
- 从概率的角度来看,逻辑回归等价于
- 建模:假设输出为伯努利条件分布
- 训练:通过最大化对数似然来训练模型
- 从概率的角度来看,多类分类问题等价于
- 建模:假设输出为类别分布
- 训练:通过最大化对数似然来训练模型
Lec 04 非线性模型,过拟合和正则化
- 线性模型非线性化:使用基函数非线性化线性模型:$f(\mathbf x) = \Phi(\mathbf x)\mathbf w$
- \[[x_1, x_2, ...,x_m] \in \mathbb R^m \to [\phi_1(\mathbf x), \phi_2(\mathbf x), ..., \phi_n(\mathbf x)] \in \mathbb R^n\]
- 损失函数:$L(\mathbf w) = \frac1N\mid \mid \Phi(\mathbf{X})\mathbf w - \mathbf y\mid \mid ^2$,$\mathbf w^* = (\Phi^T\Phi)^{-1}\Phi^T\mathbf y$
-
交叉熵存实函数:同理把原来线性公式中的$\mathbf x^{(i)}$ 替换成 $\Phi^{(i)}$ 即可
-
过拟合:指模型在训练集上表现很好(损失函数绩极小),到了验证和测试阶段就很差,即模型的泛化能力很差。原因:数据量太少而模型太复杂
- 模型的泛化能力:模型能够很好地处理(拟合)不可见数据的能力称为模型的泛化能力
- 欠拟合:指模型在训练集、验证集和测试集上均表现不佳的情况,原因:模型复杂度过低;特征量过少
- 模型的选择:给定若干模型,选择出能在不可见的测试集上表现最好的模型。
- 验证集:留出一部分(20% ~ 30%)训练数据作为验证集,剩下的作为训练数据。在训练集上训练模型,在等待验证集上对模型进行评估;在验证集中选择性能最好的模型
- 交叉验证(K-Fold):将整个训练集划分成 K 个子集,每次取 K -1 个子集作为训练集进行训练,剩下的子集作为验证集,重复 K 次。
-
正则化:除了拟合训练数据外,对参数施加一些先验偏好
-
L2 正则化: \(\tilde L(\mathbf w) = L(\mathbf w) + \lambda \mid \mid \mathbf w\mid \mid _2^2, \mid \mid \mathbf w\mid \mid _2 = (\sum_{k = 1}^K w_k^2)^\frac{1}{2}\)
- 倾于将模型参数缩小到零;$\lambda$ 越大,说明 $\mathbf w$ 对小值的偏好越强
-
L1 正则化: \(\tilde L(\mathbf w) = L(\mathbf w) + \lambda \mid \mid \mathbf w\mid \mid _1, \mid \mid \mathbf w\mid \mid _1 = \sum_{k = 1}^K \mid w_k\mid\)
- L1 正则化也倾于使用较小的模型参数值,但经常导致 $\mathbf w$ 稀疏解,即 $\mathbf w$ 中的许多元素都是零
-
Lec 05 支持向量机 SVM
-
线性分类器的判决边界:\(\left. \{ \mathbf x\mid \mathbf w^{*^T} \mathbf x + b^* = 0\right.\}\),判决边界是与 \(\mathbf w^*\) 垂直的超平面,与原点的距离是 \(-\frac{b^*}{\mid \mid \mathbf w^*\mid \mid }\)
-
最大边界分类器 Maximum-Margin Classifier:找到一个超平面使得边界尽可能大
- 边界:边界用样本点到超平面的最小距离表示 \(Margin = \min_{l}\frac{y^{(l)}\cdot(\mathbf{w}^T\mathbf x^{(l)} + b)}{||\mathbf w||}\)
-
最大边界分类的问题描述:
\[\mathbf w^*, b^* = \arg\max_{\mathbf w,b} \{ \frac{1}{||\mathbf w||} \min_{l} [y^{(l)}\cdot(\mathbf{w}^T\mathbf x^{(l)} + b)]\}\]-
推导过程:(下面懒得给向量加粗)
- 将 $x$ 分解为 $m_1, m_2$,其中 $m_2$ 与超平面垂直,即 $m_2 \mid \mid w$,$m_1$ 在在超平面上,即满足 $w^Tm_1 + b = 0$;
- 从而计算 $w^Tx + b = w^T(m_1 + m_2)+ b = w^Tm_2$,令这个式子为 $h(x)$;
- 又因为 $m_2\mid \mid w$,$m_2$ 可以写成 $m_2 = \gamma \cdot \frac{w}{\mid \mid w\mid \mid }$(前者表示长度,后者表示方向);
- 将 $m_2$ 代入 $h(x)$,有 $ h(x) = \gamma \cdot\frac{w^Tw}{\mid \mid w\mid \mid } = \gamma \cdot \mid \mid w\mid \mid $,变形得到$\gamma = \frac{h(x)}{\mid \mid w\mid \mid }$;
- 因为 $\gamma$ 表示距离,在超平面的另一端,$h(x)$ 为负数,故此是要乘以 $-1$,负负得正;
- 最后得到:\(\gamma = \frac{y\cdot h(x)}{\mid \mid w\mid \mid } = \frac{y\cdot(w^Tx+b)}{\mid \mid w\mid \mid }, y \in \{-1, 1\}\)
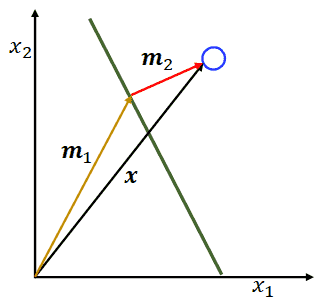
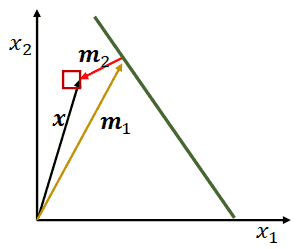
-
最大边界分类的等价对偶函数:优化另一个目标函数,与原始问题具有相同的优化值,转化成的目标函数如下(凸二次优化问题,数值方法可求出最优解):
\[\min_{\mathbf w,b}\frac12||\mathbf w||^2 \\ \text{s.t. }y^{(l)}\cdot(\mathbf w^T\mathbf x^{(l)} + b) \ge 1, \text{ for } l = 1,2,...,N\] -
原始优化问题的拉格朗日函数:拉格朗日乘子 $a_l$ 满足 $a_l \ge 0$
\[L(\mathbf w,b,\mathbf a) = \frac12||\mathbf w||^2-\sum_{l = 1}^{N}a_l(y^{(l)}(\mathbf w^T \mathbf x^{(l)} + b)-1)\] -
拉格朗日对偶函数:
\[g(\mathbf a) = \min_{\mathbf w,b}L(\mathbf w,b,\mathbf a) \\\] -
原优化问题的对偶公式
\[\max_{\mathbf a} g(\mathbf a) \\ \text{s.t. } a \ge 0\] -
推导函数 $g(\mathbf a)$ 的近似表达式(又称解析解),即消去公式中的 $\mathbf w, b$ 。
-
通过计算梯度:$\frac{\partial L}{\partial \mathbf w} = 0$ 和 $\frac{\partial L}{\partial b} = 0$,得到的式子再代入 $g(\mathbf a)$ 中(计算的秘诀是看清楚标量向量,向量点乘)
\[\mathbf w = \sum_{l = 1}^N a_ly^{(l)}\mathbf x^{l}, \sum _{l=1}^Na_ly^{(l)}= 0 \\\]得到:
\[g(\mathbf a) = \sum_{l=1}^Na_l-\frac12\sum_{l=1}^N\sum_{j=1}^Na_la_jy^{(l)}y^{(j)}\mathbf x^{(l)^T}\mathbf x^{(j)}\] -
对偶优化变成:该式子可以使用数值优化
\[\max_{\mathbf a} g(\mathbf a) = \max_a (\sum_{l=1}^Na_l-\frac12\sum_{l=1}^N\sum_{j=1}^Na_la_jy^{(l)}y^{(j)}\mathbf x^{(l)^T}\mathbf x^{(j)})\\ \text{s.t. } a \ge 0 \text{ and } \sum_{l=1}^Na_ly^{(l)}= 0\] -
计算 \(\mathbf a^*\) 后转化为 \(\mathbf w^*, b^*\)
\[\mathbf w^* =\sum_{l = 1}^N a_l^*y^{(l)}\mathbf x^{(l)}\]对于每一个在边界 $S$ 上的样本 $(\mathbf x^{(i)}, y^{(i)})$ ,有 \(y^{(i)}(\mathbf w^{*^T}\mathbf x^{(i)} + b^*) = 1\),可以解出 \(b^*\),最后可以对所有边界样本求出的结果取均值:
\[b^* = \frac1{|S|}\sum_{i \in S}(y^{(i)} - \mathbf w^{*^T}\mathbf x^{(i)}) = \frac1{|S|}\sum_{i \in S}(y^{(i)} - \sum_{l = 1}^N a_l^*y^{(l)}\mathbf x^{(l)^T}\mathbf x^{(i)})\] -
最后将 \(\mathbf w^*, b^*\) 代入回 \(\hat y(\mathbf x)=sign(\mathbf w^{*^T}\mathbf x + b^*)\) 即可得到对偶的最大边界分类器:
\[\hat y(\mathbf x) = sign(\sum_{n = 1}^N a_n^*y^{(n)}\mathbf x^{(n)^T}\mathbf x + b^*)\]
-
-
支持向量:满足 \(y^{(n)}(\mathbf w^{*^T} \mathbf x^{(n)} + b^*) = 1\) 的样本 \(\mathbf x^{(n)}\),即在边界上的样本。
- 在处理测试样本时,只需要评估训练样本 $\mathbf x$ 和支持向量 $\mathbf x^{(n)}, n \in S$ 的相似性 $\mathbf x^{(n)^T}\mathbf x$
-
软最大边界分类器 Soft Maximum-Margin Classifier
-
松弛变量:引入松弛变量 $\xi_n$,解决最大边界分类器出现超平面不存在的情况。
\[y^{(n)}\cdot(\mathbf w^T\mathbf x^{(n)} + b) \ge 1 - \xi_n, \xi_n \ge 0\] -
优化任务:($C$ 是控制因子)
\[\min_{\mathbf w, b, \xi}\frac12||\mathbf{w}^2||+C\sum_{n=1}^N \xi_n \\ \text{s.t. } y^{(n)}\cdot(\mathbf w^T\mathbf x^{(n)} + b) \ge 1 - \xi_n \\ \xi_n \ge 0, \text{ for }n=1,2,...,n\] -
对偶形式:可以看到,对比最大边界分类器,只多了一个 $a_n\le C$ 的条件,其他全部一致
- 计算过程:(重点是拉格朗日函数的编写,因为多了一个$\xi_n\ge 0$的条件,引入了$\beta$)
计算偏导:$\frac{\partial L}{\partial w}, \frac{\partial L}{\partial b}, \frac{\partial L}{\partial \xi_l}$ 前两者没有变化,$\frac{\partial l}{\partial \xi_l} = C - a_l - \beta_l = 0$,从而得到 $a_n \le C$ 的条件
拉格朗日对偶的通用公式:
-
原始问题:
\[\min_{x}f(x) \\ \text{s.t. } c_i(x) \le 0, i = 1,2,...,m \\ h_j(x) = 0, j = 1,2,...,n\] -
拉格朗日对偶函数:
\[g(\alpha,\beta) = \min_{x}L(x,\alpha, \beta)=\min_x(f(x) + \sum_{i=1}^m\alpha_ic_i(x) + \sum_{j = 1}^n\beta_jh_j(x))\]
-
-
支持向量机 Support Vector Machine
-
基本模型的优化目标函数:
\[\arg\min_{w,b}\frac12||w^2|| \\ \text{s.t.} y_i (w^Tx_i+b) \ge 1, i = 1,2,...,m\] -
核函数 Kernel Function:核函数是一个双变量函数 $k(\mathbf x, \mathbf x’)$,可以表示为某个函数 $\Phi(\cdot)$ 的内积:$k(\mathbf x,\mathbf x’) = \Phi(\mathbf x)^T\Phi(\mathbf x’)$。
- 引入核函数的原因:直接使用基函数替换 $x$ 会导致计算内积时代价昂贵
- Mercer 定理:若核函数是对称正定($\int\int g(\mathbf x)k(\mathbf x, \mathbf y)g(\mathbf y)d\mathbf x d\mathbf y \ge 0, \forall g(\cdot)\in L^2$)的,则存在函数 $\Phi(\cdot)$ 满足 $k(\mathbf x, \mathbf x’) = \Phi(\mathbf x)^T\Phi(\mathbf x’)$
- 高斯核函数:$k(\mathbf x, \mathbf x’) = \exp{-\frac1{2\sigma^2}\mid \mid \mathbf x - \mathbf x’\mid \mid ^2}$,可以实现无限维非线性最大边缘分类器
-
对偶软最大边界分类器可以写成:
\[\max_\mathbf a g(\mathbf a) \\ \text{ s.t. } a_n \ge 0, a_n \le C, \sum_{n=1}^Na_ny^{(n)}=0 \\ \text{ where } g(\mathbf a)=\sum_{n=1}^Na_n-\frac12 \sum_{n=1}^N \sum_{m=1}^Na_na_m y^{(n)}y^{(m)}k(\mathbf x^{(n)}, \mathbf x^{(m)})\]测试时有:
\[\hat y(\mathbf x) = sign(\sum_{n = 1}^N a_n^*y^{(n)}k(\mathbf x^{(n)},\mathbf x) + b^*)\]
-
Lec 06 神经网络
- 回归核分类的神经网络表示:(其中 $a$ 表示激活函数,$W_l$ 表示第 $l$ 层的参数)
- 回归:$\hat y(\mathbf x) = \mathbf W_L a(…a(\mathbf W_2a(\mathbf W_1x)))$
- 分类:$\hat y(\mathbf x) = softmax(\mathbf W_L a(…a(\mathbf W_2a(\mathbf W_1x))))$
-
常见激活函数:
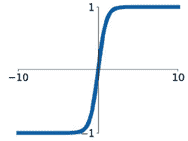
Sigmoid:$a(x) = \frac{1}{1+e^{-x}}$ Tanh:$a(x) = \frac{1-e^{-2x}}{1+e^{-2x}}$ 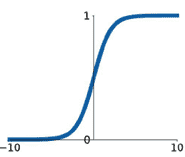
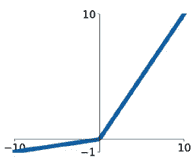
ReLU:$a(x) = max(0,x)$ Leaky ReLU:$a(x) = max(0.1x,x)$ 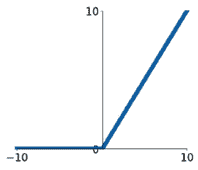
-
激活函数评价(主要围绕值域、梯度消失和计算成本)
- Sigmoid:由于饱和而梯度消失、只能输出正值、计算指数的成本较高
- Tanh:由于饱和而梯度消失、正负值都能输出、计算指数的成本较高
- ReLU:小于零时出现梯度消失、只能输出正值、计算效率高
- Leaky ReLU:不会出现梯度消失、正负值都能输出、计算效率高
-
损失函数:
- 回归:均方误差损失 $L_r(\theta) = \frac1N\sum_{(x,y)\in D}\mid y-\hat y(x)\mid ^2$
- 分类:交叉熵损失 $L_r(\theta) = \frac1N\sum_{(x,y)\in D}\sum_{k = 1}^K -y_k\log \hat y_k(x)$
-
反向传播:计算 $\frac{\partial L}{\partial \mathbf W_t}$
-
$l$ 层的前馈可以表示为:$\hat h_t = W_lh_{l-1}, h_l = a(h_l)$,即 $h_l = a(W_lh_{l-1})$
-
梯度计算(链式法则):
-
计算步骤:
- 第一步:从后往前计算$\frac{\partial L}{\partial h_l}$
- 第二部:从后往前计算$\frac{\partial L}{\partial W_l[i,j]}$
-
计算 $\frac{\partial L}{\partial W_l[i,j]}$:
\[\frac{\partial L}{\partial W_l[i,j]} = \frac{\partial L}{\partial h_{l,i}}\frac{\partial h_{l,i}}{\partial W_l[i,j]} \\= \frac{\partial L}{\partial h_{l,i}}\frac{\partial h_{l,i}}{\partial \hat h_{l,i}}\frac{\partial \hat h_{l,i}}{\partial W_l[i,j]} \\= \frac{\partial L}{\partial h_{l,i}}\frac{\partial h_{l,i}}{\partial \hat h_{l,i}}h_{l-1.j}\]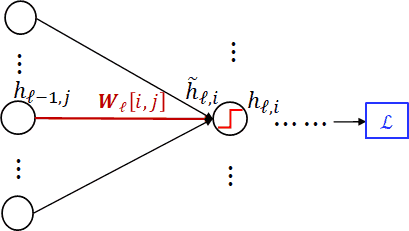
-
计算 $\frac{\partial L}{\partial h_{l,i}}$:
\[\frac{\partial L}{\partial h_{l,i}} = \sum_{j=1}^m[\frac{\partial L}{\partial h_{l+1,i}}\frac{\partial h_{l+1,i}}{\partial h_{l,i}}] \\ = \sum_{j=1}^m[\frac{\partial L}{\partial h_{l+1,i}}\frac{\partial h_{l+1,i}}{\partial \hat h_{l+1,i}}\frac{\hat h_{l+1,i}}{\partial h_{l,i}}] \\ = \sum_{j=1}^m[\frac{\partial L}{\partial h_{l+1,i}}\frac{\partial h_{l+1,i}}{\partial \hat h_{l+1,i}}W_{l+1}[j,i]]\]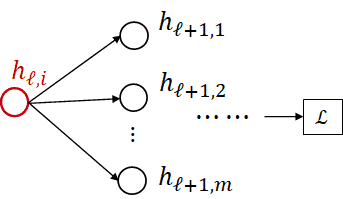
-
计算输出层:
-
回归(均方误差损失):$\frac{\partial L}{\partial h_L} = (h_L - y)$
-
分类(交叉熵损失):$\frac{\partial L}{\partial h_L} = \frac{h_L - y}{h_L(1-h_L)}$
-
-
-
经典网络结构:
- CNN:卷积、池化操作
- LeNet、AlexNet、ResNet
- GCN:图卷积网络、GraphAttentionNetwork 图注意力网络
- RNN
- CNN:卷积、池化操作
-
Lec 07 神经网络的优化和训练技巧
-
算法优化:
-
随机梯度下降 SGD
\[w_{t+1}=w_t-lr\times\nabla f(w_t)\]- $\nabla f(w_t)$:损失函数 L 的随机梯度
-
SGD + 动量:
\[v_t = \rho v_{t-1} + \nabla f(w_t) \\ w_{t+1}=w_t-lr\times v_t\]- $\rho\in(0,1)$:退化率
-
RMSProp
\[s_t = \rho\times s_{t-1} + (1-\rho)(\nabla f(w_t) \odot \nabla f(w_t)) \\ w_{t+1}=w_t-lr\times\nabla f(w_t) \oslash\sqrt{s_t}\]- $s_t$:累计平方梯度,$\odot$ 逐元素乘法,$\oslash$ 逐元素除法
-
Adam
\[m_t = \beta_1 \times m_{t-1} + (1-\beta_1)\nabla f(w_t) \\ s_t = \beta_2\times s_{t-1} + (1-\beta_2)(\nabla f(w_t) \odot \nabla f(w_t)) \\ w_{t+1}=w_t-lr\times m_t \oslash\sqrt{s_t}\]- $m_t$:历史梯度的移动平均
-
-
训练技巧
-
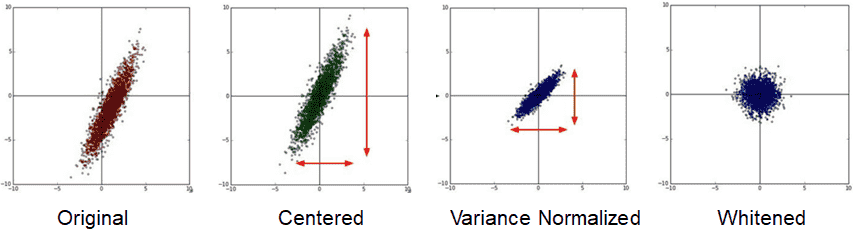
预处理:
-
中心化(减均值)、归一化(Normalizing the variance 除方差)、白化(Whitening)
-
-
初始化:使用高斯分布($N(0,0.01^2)$)来随机化权重参数,随着网络层数加深,可以使用 $N(0,\sigma_i^2)$ 的高斯分布,使得每一层的方差与前一层的神经元数量成反比
-
超参数微调:在开始训练之前有很多参数需要设置,为了给这些超参数设置合适的值,将整个数据集分成三部分,即训练集、验证集和测试集,分别用于训练模型、调整超参、测试最终性能。
-
Lec 08 集成学习:Bagging & Boosting
- 集成的思想:训练一堆弱分类器,这些分类器可能只在数据集的一部分上表现良好,如果将在不同部分上表现良好的弱分类器结合在一起,就可以得到一个强分类器。
- 结合的思路:使用投票机制或投票,更优秀的分类器有更高的权重
- Bagging:首先通过 Bootstrapping 创建训练数据集的子集(有放回采样),然后在每个子集上训练一棵决策树(或者其他模型),最后通过多数投票将决策树们合并为一个决策树(或者其他模型)
- 随机森林:在构建决策树时,只使用随机属性子集
- Boosting:
- 弱分类器创建:重复执行以下步骤:识别被错误分类的例子,重新训练分类器,对错误分类的例子给予更多的权重
- 弱分类器合并:将各分类器的预测结果进行加权平均
- Adaboost 算法:(以二分类问题为例)
- 迭代:计算第一个分类器 $h_1$ 上的错误率 $\epsilon_1$,并为此分类器赋予权值 $\alpha_1 = \frac12\ln(\frac{1-\epsilon_1}{\epsilon_1})$。最开始的时候,每一个样本 $x_i$ 的权重都是一样的,而现在需要将被错误分类的样本的权重以 $e^{\alpha_1}$ 的倍率增强,被正确分类的样本的权重以 $e^{-\alpha_1}$ 的倍率减弱,不断迭代计算 $h_2, h_3,…$
- 结合:每个弱分类器的输出乘以权重后加和做为最终输出。
Lec 09 线性降维 PCA
-
PCA 基本原理:通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。(高维数据经常可以使用一个低维表示来近似,即存在一个内在维度,可以保存数据的大部分信息)
-
从最小化重构误差的角度理解 PCA
-
高维空间中的正交方向是一组两两正交的(单位)向量组,正交可以表示成向量内积等于 0。
-
定理:在给定 M 个标准正交方向 $u_i$ 下,与数据样本 $x$ 的最佳近似为:$\hat {\mathbf x} = \alpha_1 \mathbf u_1 + \alpha_2 \mathbf u_2 +…+\alpha_M \mathbf u_M$, $\alpha_i = \mathbf u_i^T\mathbf x$(系数 $\alpha_i$ 可以算出,但最佳方向还未确定)。
-
目标:确定最佳方向
- 给定数据 \(\{\mathbf x^{(n)}\}_{n=1}^N \in \mathbb R^D\) ,找出最能代表原始数据的正交方向 $u_i$,即 \(\mathbf x^{(n)} \approx \sum_{i=1}^{M}\alpha_i^{(n)}\mathbf u_i\)
- 目标可以表述为最小化数据 \(\mathbf x^{(n)}\)与其近似值 \(\hat{\mathbf x}^{(n)} = \sum_{i=1}^{M}\alpha_i^{(n)}\mathbf u_i\) 之间的误差
-
推导步骤:
-
中心化样本:$\mathbf x^{(n)} - \overline {\mathbf x} = \mathbf x^{(n)} - \frac1N\sum_{n=1}^N\mathbf x^{(n)}$
-
描述目标问题:
\[E = \frac1N\sum_{n=1}^N||(\mathbf x^{(n)}-\overline{\mathbf x})-\hat{\mathbf x}^{(n)}||^2 \\ \alpha_I^{(n)} = \mathbf u_i^T(\mathbf x^{(n)}-\overline{\mathbf x})\] -
将 $ \hat{\mathbf x}^{(n)}$ 的表达式代入 $E$,并将平方展开,再将 $\alpha_i^{(n)}$ 的表达式代入展开后的 $E$ 得到:
\[E = \frac1N(\sum_{i=1}^{N}||\mathbf{x}^{(n)}-\overline{\mathbf x}||^2 - 2\sum_{n=1}^N\sum_{i=1}^M\alpha_i^{(n)}(\mathbf{x}^{(n)}-\overline{\mathbf x})^T\mathbf u_i + \sum_{n=1}^N\sum_{i=1}^M(\alpha_i^{(n)})^2) \\ E = \frac1N\sum_{i=1}^{N}||\mathbf{x}^{(n)}-\overline{\mathbf x}||^2 - \sum_{i=1}^M\mathbf u_i^T\frac1N\sum_{n=1}^N(\mathbf x^{(n)}-\overline{\mathbf x})(\mathbf x^{(n)}-\overline{\mathbf x})^T\mathbf u_i\]我们令 $s = \frac1N\sum_{n=1}^N(\mathbf x^{(n)}-\overline{\mathbf x})(\mathbf x^{(n)}-\overline{\mathbf x})^T$,$E$ 的前半部分是常数
-
-
- 将 $E$ 写成矩阵形式:
其中:$\mathbf X = [\mathbf x^{(1)}, \mathbf x^{(2)}, …, \mathbf x^{(N)}]$,$\mid \mid \cdot\mid \mid _F$ 是 Frobenius范数,定义为矩阵各项元素的绝对值平方的总和开根。
- 问题转换:
- 在 $M=1$ 的情况下,使用拉格朗日方法,可以看出 $u_1$ 应该是 $S$ 最大特征值对应的特征向量
-
在 $M = k$ 的情况下(推导同样使用拉格朗日方法,注意利用正交的条件),$u_i$ 就是 $S$ 最大的 $k$ 个特征值对应的特征向量
-
从最大化方差的角度理解 PCA:最大化方差等于尽可能保留原始数据的信息
-
推导过程:
-
以 $M=1$ 为例:
-
对于第一个方向 $u_1$,我们希望投影到 $u_1$ 方 向上的数据方差,即 $\mathbf u_1^T\mathbf x^{(n)}$,是最大的。
-
方差的表达式:
\[var = \frac1N\sum_{n=1}^N(\mathbf u_1^T(\mathbf x^{(n)}-\overline{\mathbf x}))^2 \\ = \mathbf u_1^T\frac1N\sum_{n=1}^N(\mathbf x^{(n)}-\overline{\mathbf x})(\mathbf x^{(n)}-\overline{\mathbf x})^T\mathbf u_1 \\ = \mathbf u_1^T\mathbf S\mathbf u_1\] -
同样可以推出 $u_1$ 应该是 $S$ 最大特征值对应的特征向量
-
-
在 $M = k$ 的情况下(推导同样使用拉格朗日方法,注意利用正交的条件),$u_i$ 就是 $S$ 最大的 $k$ 个特征值对应的特征向量
-
-
-
从奇异值分解 SVD 的角度理解 PCA:
-
SVD:$U,V$ 的列向量 $u_i, v_i$ 分别是 $AA^T,A^TA$ 的第 $i$ 个特征向量,$\Sigma$ 是特征值对角矩阵,是 $AA^T,A^TA$ 特征值的平方根,也是 $A$ 的特征值,并且从大到小有序排列。
\[\mathbf A = \mathbf U\Sigma \mathbf V^T = \sum_{i=1}^M\Sigma_{ii}\mathbf u_i\mathbf v_i^T\]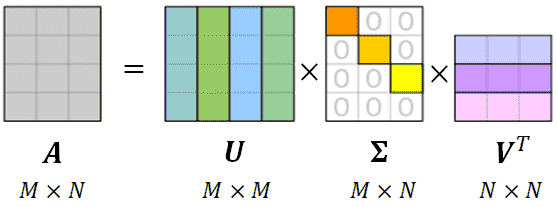
-
定义 $\hat X = [x^{(1)}-\overline x, …, x^{(N)}-\overline x]$,有$\hat X\hat X^T = \sum_{n=1}^N(x^{(n)}-\overline x)(x^{(n)}-\overline x)^T = N\cdot S$,对 $\hat X$ 做 SVD分解,就可以得到主方向。
-
计算特征值、特征向量
- 求解特征值:计算行列式 $\mid A-\lambda E\mid $,方程的根就是特征值
- 将特征向量代入方程 $(A-\lambda E)x = 0$,求解
Lec 10 K-Means 聚类
-
聚类的目标:类内高相似性和类间低相似性
-
K-Menas 算法原理:通过最小化几何点之间的平均距离将相似数据点分组成集群。以迭代方式将数据集分为 K 个非重叠集群,其中每个数据点均属于集群中心均值最近的集群。
-
K-Means 算法步骤:
-
随机初始化 K 个中心 $\mu_k, k\in {1,2,…,K}$,然后计算样本 $x^{(n)}$ 和各个中心点的距离
-
将与样本 $x^{(n)}$ 最近的中心点所在的类作为 $x^{(n)}$ 的类
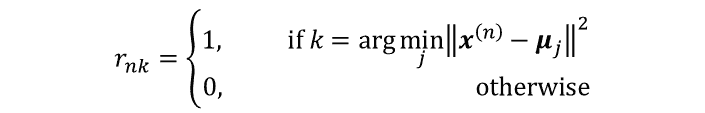
- 使用每个集群中所有样本的平均作为集群新的中心:$\mu_k \leftarrow \frac{\sum_{n=1}^Nr_{nl}\mathbf x_n}{\sum_{n=1}^Nr_{nl}}$
- 重复上面的赋值和中心更新过程,直至算法收敛,样本的类不再发生变化
-
-
算法能够收敛的证明:样本到中心点的总距离 $J$ 有下限,算法每次迭代总距离减小
-
算法讨论:
- 聚类个数 $K$ 的选择:观察总距离 J 曲线随 K 的变化曲线,选择肘点(elbow point)
- 初始点选择:
- 随机选择样本点
- 基于距离选择样本点:随机选择一个,然后接下来每次选择与已选点的平均最远的一个点
- 结合上述两种方法:每次选最远的若干点,从中随机选择一个点
- Soft K-Means:每个样本点 $x_i$ 以概率 $p_{i,j}$ 在类 $j$ 中
Lec 11 EM 算法
-
无监督分类问题,有点像 K-Means
-
问题的一般形式:给定一个联合分布 $p(x,z;\theta)$(在概率模型的参数 $\theta$ 下,$x,z$ 的联合概率分布),$x$ 是观测变量,$z$ 是隐变量(Latent variable),目标是最大化似然分布:$\theta = \arg\max_\theta\log p(x;\theta)$,满足 $ p(x;\theta) = \sum_z p(x,z;\theta)$。即我们需要根据联合概率分布函数 $p(x,z;\theta)$,优化边缘概率分布函数 $p(x;\theta)$
-
EM 算法(期望最大化算法)算法步骤:
-
E 步:评估期望(下标所示分布下,括号内的随机变量的期望)
- 假定参数已知,计算此时隐变量的后验概率(求出每一个样本属于类别的期望值)
-
M 步:更新参数
- 带入隐变量的后验概率,最大化样本分布的对数似然函数,求解相应的参数(通过当前数据求出最可能的分布参数)
-
参数说明:
-
$p(z\mid x;\theta^{(t)})$:隐变量的后验分布(条件概率)
-
$Q$:联合分布的对数 $\log p(x,z;\theta)$ 关于后验概率分布 $p(z\mid x;\theta^{(t)})$ 的期望
条件概率:$P(B\mid A) = \frac{P(AB)}{P(A)}$;
全概率公式:$P(A) = \sum_{i=1}^nP(B_i)P(A\mid B_i)$
-
-
-
EM 的证明:证明算法可以保证每一步的 likelihood 增加
\[\log p(x;\theta) = \sum_z q(z) \log \frac{p(x,z;\theta)}{p(z|x;\theta)} \\ = \sum_z q(z) \log \frac{p(x,z;\theta)}{q(z)} + \sum_z q(z) \log \frac{q(z)}{p(z|x;\theta)} \\ =L(q,\theta) + KL(q||p(z|x;\theta)), \forall \theta,q(z)\]- 其中:$KL(q\mid \mid p) = \int q(z)\log\frac{q(z)}{p(z)}dz$ 是 KL 散度,用于衡量两个分布的距离
\[L(p(z|x;\theta^{(t)}),\theta^{(t)}) = \sum_z p(z|x;\theta^{(t)})\log\frac{p(x,z;\theta^{(t)})}{p(x|z;\theta^{(t)})}\]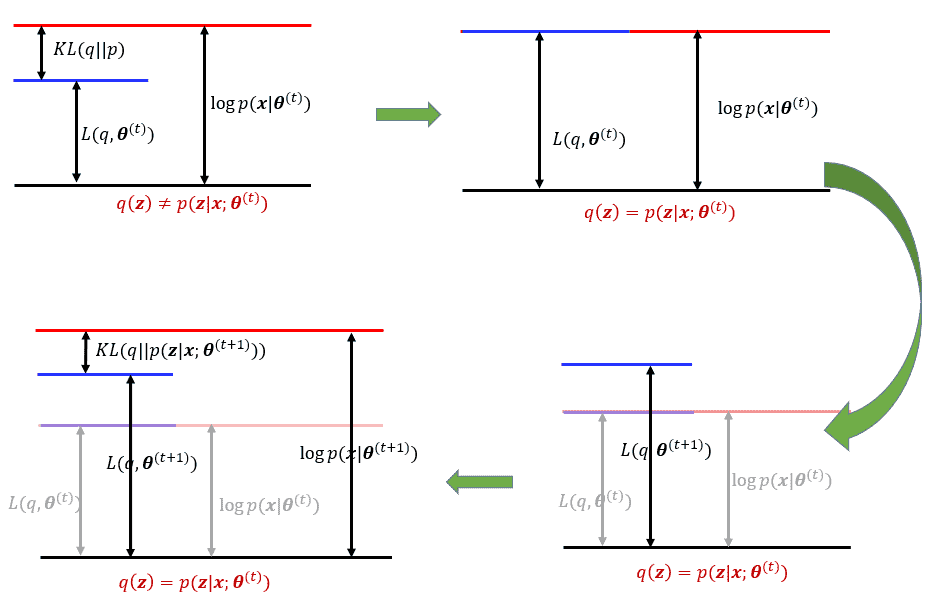
-
训练高斯混合模型的例子
-
混合高斯分布:
\[p(x) = \sum_{k=1}^{K}\pi_k\mathcal N(x;\mu_k,\Sigma_k)\]-
可以将其表示为联合分布的边缘分布(?)
\[p(x,z)=p(x|z)p(z)=\prod_{k=1}^K[\pi_k\mathcal N(x;\mu_k, \Sigma_k)]^{z_k}\]其中,$\mathbf z = [z_1, z_2, …, z_k]$ 服从分类分布,参数为 $\pi$
分类分布:$P(X=x_k\theta_1,\theta_2,…\theta_K) = \prod_{k=1}^K\theta_k^{x_k}$,其中$\sum_{k=1}^K\theta_k =1, x_k\in {0,1}, k\in {1,2,…,K}$
-
-
E 步:
-
后验分布:其中 $1_k$ 指第 $k$ 个元素为 1 的独热向量
\[p(z=1_k|x;\theta)=\frac{p(x,z=1_k;\theta)}{\sum_{i=1}^Kp(x,z=1_i;\theta)}\] -
对数联合分布:就直接在混合高斯分布上加 $\log$ 就行了
\[\log p(x,z;\theta) = \sum_{k=1}^K z_k \cdot [\log \mathcal N(x|\mu_k, \Sigma_k) + \log \pi_k]\] -
计算期望:
\[\mathbb E_{p(z|x;\theta^{(t)})}[\log p(x,z;\theta)] \\ = \sum_{k=1}^K \mathbb E_{p(z|x;\theta^{(t)})}[z_k][\log \mathcal N(x|\mu_k, \Sigma_k) + \log \pi_k]\]其中,$E_{p(z\mid x;\theta^{(t)})}[z_k]$ 用后验分布的式子代替(将混合高斯分布代入 $p$,参数加上标)
\[E_{p(z|x;\theta^{(t)})}[z_k] = \frac{\mathcal N(x|\mu_k^{(t)}, \Sigma_k^{(t)})\pi_k}{\sum_{i=1}^K \mathcal N(x|\mu_i^{(t)}, \Sigma_i^{(t)})\pi_i} = \gamma_k^{(t)}\]最后代入到 $Q(\theta;\theta^{(t)})$:
\[Q(\theta;\theta^{(t)})=\sum_{k=1}^K \gamma_k^{(t)} [\log \mathcal N(x|\mu_k, \Sigma_k) + \log \pi_k]\] -
将 $\mathcal N(x\mid \mu_k,\Sigma_k) = \frac1{(2\pi)^{D/2}\mid \sigma\mid ^{1/2}}\exp{-\frac12(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k)}$ 代入 $Q(\theta;\theta^{(t)})$:
\[Q(\theta;\theta^{(t)})= \sum_{k=1}^K\gamma_k^{(t)} [-\frac12(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k)-\frac12|\Sigma_k| + \log \pi_k] + C\]$C$ 是常量($\frac{1}{(2\pi)^{D/2}}$ 部分)
-
最后,考虑所有样本:
\[Q(\theta;\theta^{(t)})= \frac1N\sum_{n=1}^{N}\sum_{k=1}^K \gamma_k^{(t)} [-\frac12(x^{(n)}-\mu_k)^T\Sigma_k^{-1}(x^{(n)}-\mu_k)-\frac12|\Sigma_k| + \log \pi_k] + C\]
-
-
M 步:通过对 $\mu_k, \Sigma_k, \pi_k$ 求导并将它们设为零,得到最佳 $\theta$:
其中:$N_k = \sum_{n=1}^{N}\gamma_{nk}$,分配给第 $k$ 类的样本数
-
-
训练高斯混合模型的EM算法总结:
-
给定当前估算值:${\mu_k, \Sigma_k, \pi_k}{k=1}^K$,更新 $\gamma{nk}$ :
\[\gamma_{nk} \leftarrow \frac{\mathcal N(x|\mu_k,\Sigma_k)\pi_k}{\sum_{i=1}^{K}\mathcal N(x|\mu_i,\Sigma_i)\pi_i}\] -
跟据 $\gamma_{nk}$,更新 $\mu_k, \Sigma_k, \pi_k$
\[N_k \leftarrow \sum_{n=1}^N\gamma_{nk} \\ \mu_{k} \leftarrow \frac1{N_k}\sum_{n=1}^N\gamma_{nk}x_n \\ \Sigma_k \leftarrow \frac{1}{N_k}\sum_{n=1}^{N}\gamma_{nk}(x_n-\mu_k)(x_n-\mu_k)^T \\ \pi_k \leftarrow \frac{N_k}{N}\]
-
-
二维高斯混合模型EM算法的例子:EM算法视频
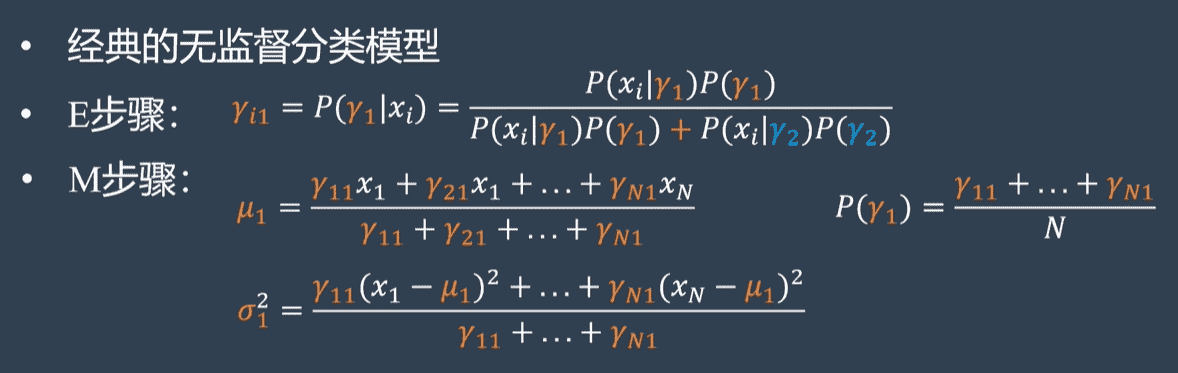
Lec 12 推荐系统:基于内容的推荐和协同滤波
-
推荐系统问题:推荐系统问题旨在用户推荐相关项,项可以是用户未观看过的电影、书籍,未访问过的网站,可以是任何可以购买的产品,实现一种个性化的推荐。推荐系统可以总结为以下模型:
\[\text{Utility Function: } u: X \times S \to R\]其中,$X$ 是用户的集合,$S$ 是项的集合,$R$ 是用户对项评分的集合,并且是关于项的有序集。
-
推荐系统问题关键问题:如何为矩阵收集已知的评级,如何从已知的评级中推断未知的评级,如何评估推断的好坏。
-
冷启动问题:项没有被评分,用户的评分记录为空。
-
-
基于内容的推荐系统:向客户推荐与用户之前评价较高的产品相似的产品
-
跟据用户对项的评分建立项的画像(特征向量),在建立用户画像(特征向量),根据用户画像推荐项(计算相似度)。
-
项的画像:一个特征向量
-
例如文本挖掘使用TF-IDF,即项的频率乘以逆文档频率
\[f_{ij} = \text{项 i 在文档 j 的出现频率} \\ TF_{ij} = \frac{f_{ij}}{\max_k f_{kj}} \\ n_i = \text{出现项 i 的文档的数目} \\ IDF_i = \log\frac N{n_i} \\ w_{ij} = TF_{ij}\times IDF_{i}\]
-
-
用户画像:例如评分项画像的加权平均
- 给定项画像 $i$ 和用户画像 $x$,可以使用余弦相似度评估:$u(x,i)=\cos(x,i)=\frac{x\cdot i}{\mid \mid x\mid \mid \cdot\mid \mid i\mid \mid }$
-
基于内容的推荐系统的优点:
- 不需要其他用户的数据,没有冷启动和稀疏性问题
- 能够推荐给口味独特的用户
- 能够推荐新的和不受欢迎的项目,没有 First-Rater 问题
- 有很好的可解释性:它可以通过列出导致项目被推荐的内容-功能来提供推荐项目的解释
-
基于内容的推荐系统的缺点:
- 难以找到合适的特征向量
- 难以向新用户推荐项,因为新用户没有用户画像
- 过度专门化:永远不会推荐用户兴趣之外的项,同时难以处理人多种信兴趣爱好的问题;无法利用其它用户进行推荐质量的评估
-
-
基于协同滤波的推荐算法
-
基于用户的协同滤波算法:找出评分与用户 $x$ 评分相似的其他用户的集合,根据集合中用户的评分估计用户 $x$ 对项的评分。
-
第一步:读取用户-项的评分矩阵 $R$。
-
第二步:跟据评分矩阵计算用户相似度矩阵 $S_U$,在计算相似度时我们选择皮尔森相关系数。我们可以将计算出的评分矩阵保存在文件中,以免下次重复计算。
-
第三步:假定我们要预测用户 $u$ 给项 $i$ 的评分。首先找到于目标用户最相似的 K 个用户 $U_{sim}$,并且这些用户对项 $i$ 有评分记录,根据以下公式计算预测评分:
\[r_{u,i} = \frac{\sum_{v \in U_{sim}} s_{u,v}r_{v,i}}{\sum_{v \in U_{sim}} s_{u,v}}\]其中,$r_{u,i}$ 指用户 $u$ 对项 $i$ 的预测评分,$s_{u,v}$ 指用户 $u$ 和用户 $v$ 的相似度。
-
-
基于项的协同滤波算法
-
第一步:读取用户-项的评分矩阵 $R$。
-
第二步:跟据评分矩阵计算用户相似度矩阵 $S_I$,在计算相似度时我们选择皮尔森相关系数。我们可以将计算出的评分矩阵保存在文件中,以免下次重复计算。
-
第三步:假定我们要预测用户 $u$ 给项 $i$ 的评分。首先找到于目标项最相似的 K 个项 $I_{sim}$,并且用户 $u$ 对这些项有评分记录,根据以下公式计算预测评分:
\[r_{u,i} = \frac{\sum_{j \in I_{sim}} s_{i,j}r_{v,i}}{\sum_{j \in I_{sim}} s_{i,j}}\]其中,$r_{u,i}$ 指用户 $u$ 对项 $i$ 的预测评分,$s_{i,j}$ 指项 $i$ 和项 $j$ 的相似度。
-
-
计算相关性的几种方法:
-
Jaccard:两个集合A和B交集元素的个数在A、B并集中所占的比例
-
Cosine:$\cos(i,j)=\frac{i\cdot j}{\mid \mid i\mid \mid \cdot\mid \mid j\mid \mid }$
-
Pearson:
\[sim(x,y) = \frac{\sum_{s\in S_{xy}}({r_{xs}-\overline r_x})({r_{ys}-\overline r_y})}{\sqrt{\sum_{s\in S_{xy}(r_{xs}-\overline r_x)^2}}\sqrt{\sum_{s\in S_{xy}(r_{ys}-\overline r_y)^2}}}\]
-
-
协同滤波算法的评价
- 适用场景:
- 基于用户的协同滤波算法:具备更强的社交特性,适用于用户少物品多,时效性较强的场景。比如新闻、博客、微内容推荐场景。此外基于用户的协同滤波算法能够为用户发现新的兴趣爱好。
- 基于项的协同滤波算法:更适用于兴趣变化较为稳定的应用,更接近于个性化的推荐,适合物品少用户多,用户兴趣固定持久,物品更新速度不是太快的场合,比如电影推荐。
- 协同滤波算法的优点:适用于任何类型的项,不需要特征选择
- 协同滤波算法的缺点:
- 冷启动问题:对于基于用户的协同滤波算法,需要积累足够多的用户,并且用户有一定评分时才能找到一个用户的相似用户,而基于项的协同滤波算法没有此问题。
- 稀疏性问题:项的数目一般很多,一个用户对项的评分往往不会很多,评分矩阵是稀疏的,难以找到对相同的项评分过的用户。
- First-Rater 问题
- 新的项、评分较少的项因为评分较少,难以被推荐。
- 冷启动问题:
- 用户冷启动:如何给新用户做个性化推荐
- 物品冷启动:如何将新的物品推荐给可能对它感兴趣的用户
- 系统冷启动:如何在新开发的网站(无用户,用户行为,只有部分物品信息)上设计个性化推荐系统,从而使得网站刚发布时就让用户体会到个性化推荐。
- 冷启动的解决方案:
- 提供非个性化推荐,比如说热门排行榜,等用户数据收集到一定的时候,切换为个性化推荐
- 利用用户注册信息,人口统计学信息;用户兴趣描述;从其它网站导入的用户站外行为等。
- 选择合适的物品启动用户的兴趣,用户登录时对一些物品进行反馈,收集用户对这些物品的兴趣信息,然后给用户推荐和这些物品相似的物品。
- 利用物品的内容信息,userCF算法需要解决第一推动力的问题,第一个用户从哪里发现新物品。考虑利用物品的内容信息,将新物品先投放给曾经喜欢过和它内容相似的其他物品的用户。对于itemCF,只能利用物品的内容信息计算物品的相关程度。基本思路就是将物品转换为关键词向量,通过计算向量之间的相似度(如余弦相似度),得到物品的相关程度。
- 采用专家标注,针对很多系统在建立的时候,既没有用户的行为数据,也没有充足的物品内容信息来计算物品相似度,这时就需要利用专家标注。
- 利用用户在其他地方已经沉淀的数据进行冷启动,比如引导用户通过社交网络账号登录,一方面降低注册成本提高转化率,另一方面获取用户的社交网络信息,解决冷启动问题。
- 利用用户的手机等兴趣偏好进行冷启动:Android手机开放的比较高,所以在安装自己的app时,就可以顺路了解下手机上还安装了什么其他的app。然后可以总结用户的特点和类型。
- 适用场景:
-
评估指标
- RMSE:(测试样本的)均方误差
-
-
基于矩阵分解的推荐系统
本篇复习笔记参考自一位师兄/师姐的笔记,特此感谢。