高斯混合聚类GMM
在讲高斯混合聚类算法之前先补充以下相关的数学知识,由于篇幅原因,只是简单叙述,如需详细内容,请查阅相关资料
一、正态分布
在概率论中我们学过某些数值在一定情况下是符合正态分布的。
我们经常见到某某数据符合正态分布,那么它到底是什么意思呢?
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。 若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

正态分布是许多统计方法的理论基础。检验、方差分析、相关和回归分析等多种统计方法均要求分析的指标服从正态分布。许多统计方法虽然不要求分析指标服从正态分布,但相应的统计量在大样本时近似正态分布,因而大样本时这些统计推断方法也是以正态分布为理论基础的。
为什么很多假设都是使用正态分布呢?为什么不适用像泊松分布、指数分布这些分布呢?
- 根据中心极限定律,如果我们的样本足够多的情况下,我们的数据是符合正态分布的
- 正态分布是属于一种正态分布,具有良好的数学性质,便于建模
1.一元正态分布
一元正态分布的概率密度为:
\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]我们记作 $ N(\mu,\sigma^2)$,其中$\mu$ 为数据的均值,而 $\sigma^2$ 为样本的方差,f(x)为概率密度,进行积分后值为1。
2.二元正态分布
二元正态分布的概率密度为:
\[f(x_1,x_2)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}e^{\frac{-1}{2(1-\rho^2)^2}\{\frac{(x_1-\mu_1)^2}{\sigma_1^2}-2\rho\frac{(x_1-\mu_1)(x_2-\mu_2)}{\sigma_1\sigma_2}+\frac{(x_2-\mu_2)^2}{\sigma_2^2}\}}\]常记作$N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$,分别对应着两个随机变量的均值和方差,以及两个随机变量之间的相关系数。
3.多元正态分布
多元正态分布的概率密度为:
\[f(X)=\frac{1}{(2\pi)^{\frac{n}{2}}|\sum|^{\frac{1}{2}}}e^{-\frac{1}{2}(X-\mu)^T\sum^-1(X-\mu)}\]上面式子中的 $ \mu$为n维均值向量,形状为 (n,1),$ \sum$为随机变量X的协方差矩阵。
该式子为一元正态分布的推广公式,涉及到多维变量,用矩阵进行表示。
4.概率密度函数
我们发现上面的三个式子中存在两种变量,一种是数据X,另外一种就是参数 $\mu$和 $ \sigma$ ,也就是分布的参数。对于概率来说,我们是已知模型分布和参数,然后带入数据去求概率,而概率统计是已知分布,但是不知道分布符合的参数,然后基于样本数据X去估计分布的参数,使用的方法就是极大似然估计。
5.极大似然估计
什么是极大似然估计?
上面我们说有些情况,我们只是知道数据符合的分布,但是不知道具体符合的参数为多少,就是我们只知道某某数据符合正态分布,但是正态分布的均值和方差我们是不知道的,所以要根据已有样本进行估计,其实就是将所有样本数据带入概率密度公式,会获得每个数据的概率,然后将各概率相乘,最终优化就是使该式子达到最大,为什么是最大?因为我们的数据符合该分布,也就是要我们的样本数据大概率的出现在该分布中,然后求出使概率乘积最大的参数。
二、高斯混合聚类
说了这么久,终于到了我们的主题,就是我们的高斯混合聚类。
它是一种基于概率分布的聚类算法,它是首先假设每个簇符合不同的高斯分布,也就是多元正态分布,说白了就是每个簇内的数据会符合一定的数据分布。
它的大致流程就是首先假设k个高斯分布,然后判断每个样本符合各个分布的概率,将该样本划为概率最大的那个分布簇内,然后一轮后,进行更新我们的高斯分布参数,就会用到我们的极大似然估计,然后再基于新的分布去计算符合各个分布的概率,不断迭代更新,直至模型收敛达到局部最优解,常见的算法就是EM算法,它会同时估计出每个样本所属的簇类别以及每个簇的概率分布的参数。
概率密度常记为:
\[f(X)=p(x|\mu_i,\sum)\]意思就是在参数为一定值的情况下符合的分布,对应相应的概率密度函数。
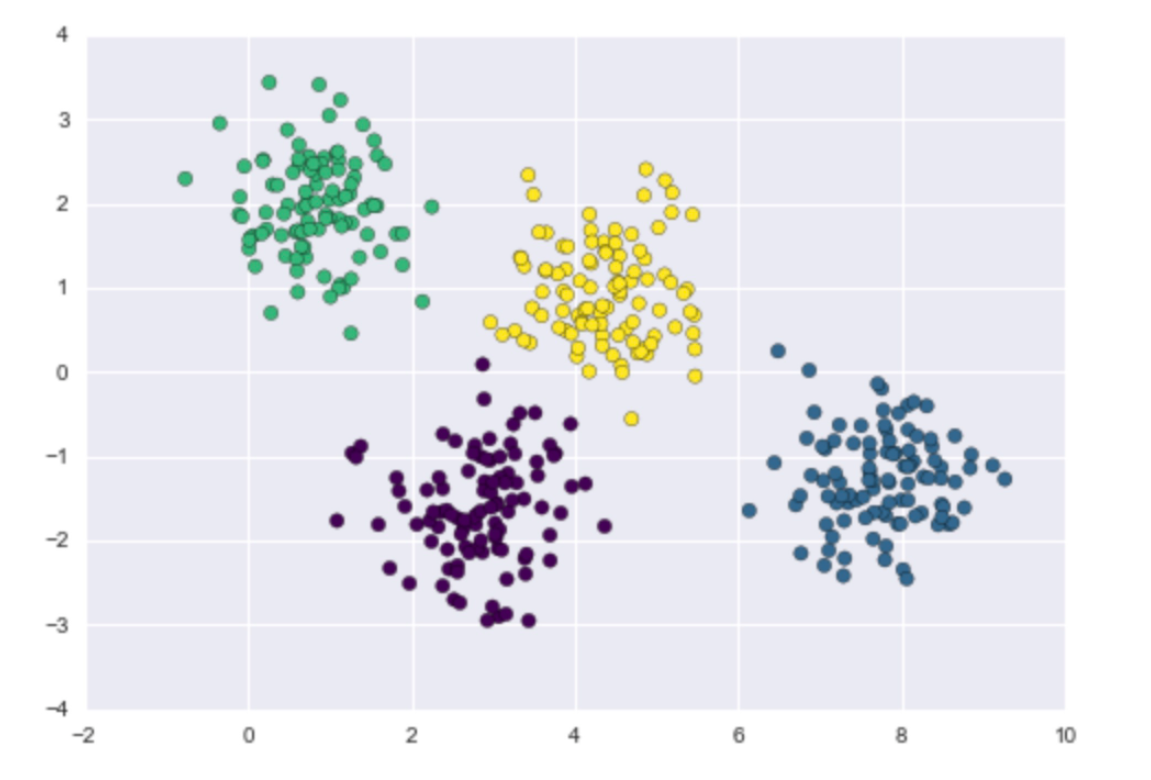
有了上述的铺垫之后,我们就可以定义聚类需要的高斯混合分布函数:
\[p(X)=\sum_{i=1}^k\alpha_ip(X\mid \mu_i,\sum_i)\]其中 $ \alpha$ 就代表我们选择每个簇的概率,那么它的和肯定是等于1的,$sum_{i=1}^k\alpha_i=1$ 。$p(X\mid \mu_i,\sum_i)$表示第i的簇内的概率分布,也就是下文中$p(x_j\mid z_j=i)$
我们现在想计算对于某一个数据符合哪个簇的概率,如果对应哪个簇的概率大,那么该数据就划分为该簇内,也就对应条件概率$ p(Z\mid x) $,意思就是在x的前提,符合哪个分布的概率。
选择第i个簇的概率是$ p(z_i=i)=\alpha_i$
我们引入几个变量,$ z_i$代表我们选择某个分布的随机变量,那么取值肯定是1-k之间,很显然它是对应我们上面的 $ \alpha$ 的,也就是$ p(z_i=i)=\alpha_i$,所以我们最终的条件概率公式为(根据贝叶斯公式):
\[\gamma_{ji}=p(z_j=i|x_j)=\frac{P(z_j=i)p(x_j|z_j=i)}{p(x_j)} =\frac{\alpha_ip(x_j|\mu_i,\sum)}{\sum_{l=1}^k\alpha_lp(x_j|\mu_l,\sum)}\]对公式的分析

该公式的意思就是我们的某一样本符合某一分布的概率,记为$\gamma_{ji}$ ,意思是数据 $j$(数据j即为第j个数据)符合分布$ i$(分布i即为第i个簇内的分布)的概率,所以我们就是要求:
\[\lambda_j=argmax_{i\in \{1,2,...k\}}\gamma_{ji}\]我们会求出数据 $ j$符合每个分布的概率,然后获得之中最大的概率,那么数据$ j$就会被划分到与之对应的簇。
但是问题来了,在求该概率时,公式分子和分母都存在某一分布的概率密度,我们只是知道符合高斯分布,但是具体的参数(均值$ \mu$和协方差矩阵$\sum$)是不知道的,那么怎么获得概率密度函数呢?
$\gamma_{ji}$ ,意思是数据 $j$(数据j即为第j个数据)符合分布$ i$(分布i即为第i个簇内的分布)的概率
上面说到了,采用极大似然的方式,就是我们的样本数据出现在对应分布的概率乘积达到最大,所以我们就要进行最大化似然:(m为样本个数?)
\[LL(D)=ln(\prod_{j=1}^mp(x_j))=\sum_{j=1}^mln(\sum_{i=1}^k\alpha_ip(x_j|u_i,\sum))\]极大似然思想在后面有介绍
对上述函数进行求导,然后另导数为0,分别求出对应的 $\mu$ ,和$ \sum$。
这些参数通常通过期望最大化(Expectation Maximization,EM)算法进行估计。
在 E 步中,计算每个数据点属于每个混合成分的概率;($\alpha$)
在 M 步中,更新混合成分的参数以最大化似然函数。($\mu$ 和$ \sum$)
然后求得:
\[\mu_i=\frac{\sum_{j=1}^m\gamma_{ji}x_j}{\sum_{j=1}^m\gamma_{ji}}\] \[\sum_i=\frac{\sum_{j=1}^m\gamma_{ji}(x_j-\mu_i)(x_j-\mu_i)^T}{\sum_{j=1}^m\gamma_{ji}}\]但是在求对应高斯混合系数$\alpha$ 时,会有约束条件,就是 $a_i\geq0,\sum_{i=1}^k\alpha_i=1$,所以我们需要对原方程添加个拉格朗日乘子。
拉格朗日乘法得基本形态就是:
对于函数 $z=f(x,y)$,在满足$\psi(x,y)=0$ 时得条件极值,可以转化为:
\[f(x,y)+\lambda\psi(x,y)\]就是在原有的方程后面添加约束条件。
对与我们的问题就是要解方程:
\[LL(D)+\lambda(\sum_{i=1}^k\alpha_i-1)\]解得:
\[\alpha_i=\frac{1}{m}\sum_{j=1}^m\gamma_{ji}\]三、详细算法流程
下面的图是我从西瓜书中摘出来的,公式看起来有点多,下面我用简单的语言将整个流程叙述一下。

- 首先在算法开始前需要确立簇的个数k,这也就对应着k个不同的高斯分布
- 初始化每个簇的高斯分布参数,$ \mu,\sum,\alpha$,用于构建高斯混合概率密度,由于是开始还没有数据,肯定是要随机给值的
- 遍历所有的样本数据,计算每个样本符合每个分布的条件概率,即$\gamma_{ji}$
- 然后利用计算好的 $ \gamma_{ji}$去计算新的$\mu,\sum,\alpha$ ,用新的参数去更新我们的分布模型,获得新的概率密度
- 利用新的分布模型计算每个样本的条件概率,重复2-4步骤,不断地进行更新模型分布参数
- 直到模型收敛,达到一定精度,停止迭代
- 根据我们新的模型参数获取每个样本的条件概率,然后获取的最大值,即 $\lambda_j=argmax_{i\in {1,2,…k}}\gamma_{ji}$,将其划分到相应的簇中
- 结束
参考资料
本文主要参考:【机器学习】聚类算法——高斯混合聚类(理论+图解)
极大似然
参考:
本文主要参考:快速理解极大似然法
辅助理解:一文搞懂极大似然估计
极大似然法( maximum likelihood estimation,MLE )是概率统计中估算模型参数的一种很经典和重要的方法,贯穿了机器学习中生成模型(Generative model)这一大分支的始终。有一定基础的同学肯定会知道与之对立的还有另一分支判别模型(Discriminative model)。然而,今天不细说这两个模型,而是用自己的理解来谈谈极大似然法。
极大似然法是用来干嘛的?
简单地说,就是估测概率模型中的参数。比如求如下高斯概率分布模型中的 $\mu$和 $\sigma^2$ 。
\[f(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]极大似然法使用的前提条件
用它,需两个条件:
- 一个参数未知的概率分布模型。比如刚刚说的 $f(x;\mu,\sigma^2)$ ,它的形状一般如图1。然而由于参数未定,它的具体形状可能千差万别,如图2。
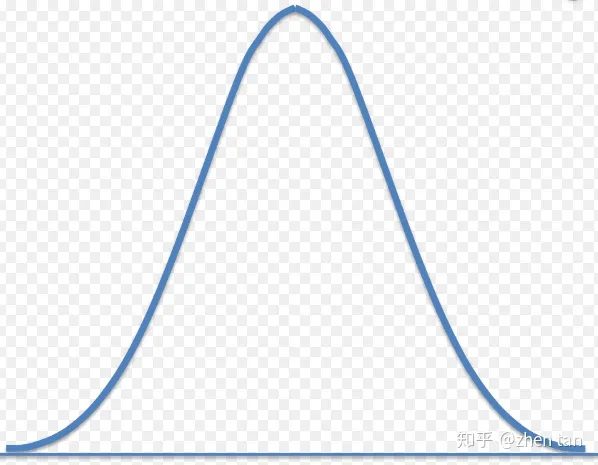
图1 参数未知的高斯模型
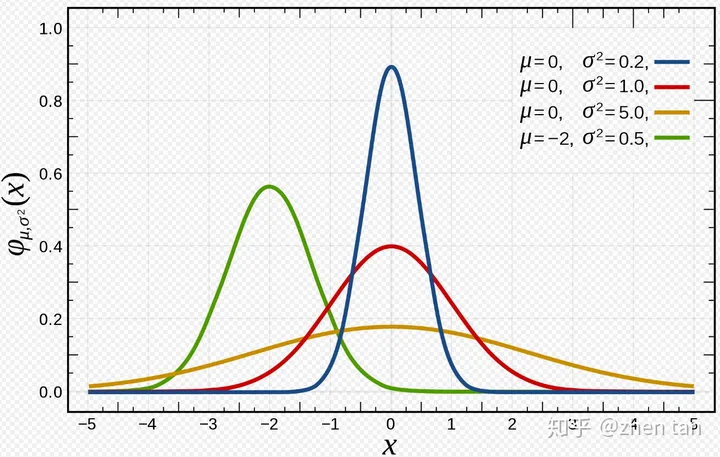
图2 不同参数下高斯分布的形状
- 一坨由该模型生成的样本点$( x_1,x_2,…,x_n )$。你可以把该模型当成一个黑盒子,它不断蹦出一系列样本点,然后你记录起来。没错,这就是采样。如图3,粉红色的曲线是女的身高模型,蓝色是男的。横坐标的蓝色点就是采样点,相信你由样本点就能轻易看出它们是由蓝色那个曲线模型生成的(男的)。极大似然法,也会用它的方式” 看 “出来。
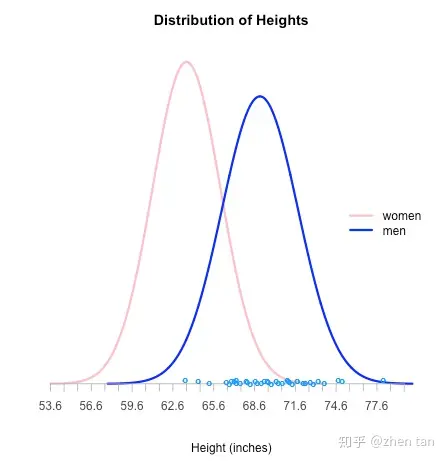
图3 采样点示例
似然函数
似然函数就是根据上面两个前提条件得到的。一言以蔽之,将那 n个样本点一个个代入未知参数的模型,然后将它们相乘即可得到似然函数。同样以高斯模型为例子,似然函数为:
\[L(\mu,\sigma^2)=f(x_1;\mu,\sigma^2)f(x_2;\mu,\sigma^2) \space \cdot\cdot\cdot \space f(x_n;\mu,\sigma^2)\\ =\prod_{i}^{n} f(x_i;\mu,\sigma^2)\]最接近真实模型的 $\mu$ 和 $\sigma^2$ 会让 $L(\mu,\sigma^2)$的值很大。这句话有两种直觉的理解方法:
- 模型容易产生大概率的样本点,小概率的样本点一般不怎么出现,所以这些样本点所对应的概率值总体是很大的,也就是它们相乘起来理应是一个很大的值。因此在 $\mu$ 和 $\sigma^2$ 的海洋中,我们需要挑出那个能使这个概率最大的参数对,这样的模型才是最契合这些样本点的,才是最有可能由该模型产生的。
- 也可以参照图3理解。可以在脑中想象,各种高矮胖瘦的高斯曲线遍布在图中不同位置。然而最有可能产生x轴上蓝色圈圈的那些采样点的肯定是其上方的那个胖度刚好的高斯函数,也就是蓝色那个。当是蓝色曲线模型时,样本点的概率相乘起来是最大的。
简单地说,我们的目标是求解出:
$( \mu^, \sigma^ )=argmaxL(\mu,\sigma^2)$
argmax的含义就是求解出让L最大的参数。
给似然函数化个妆
公式(16)实在长得太丑了,一坨相乘,实在不方便处理。由于是求最大, 所以可以给似然函数等价地加 $ln(⋅)$ ,就可以由相乘变为相加:
\[L(\mu,\sigma^2)=ln[f(x_1;\mu,\sigma^2)f(x_2;\mu,\sigma^2) \space \cdot\cdot\cdot \space f(x_n;\mu,\sigma^2)]\\ =\sum_{i}^{n} ln[f(x_i;\mu,\sigma^2)]\]求解最优参数 $( \mu^, \sigma^ )$
求解就一句话,求导置0,解方程组。
\[\begin{aligned}\frac{\partial L(\mu,\sigma^2)}{\partial\mu}&=0\\\frac{\partial L(\mu,\sigma^2)}{\partial\sigma}&=0\end{aligned}\]求解细节不说了,思想打通了就行。