模拟退火和遗传算法求解TSP问题
一、 实验题目
在TSPLIB中选一个大于100个城市数的TSP问题,使用模拟退火和遗传算法求解。我选择的是lin105.tsp
TSP问题
假设有一个旅行商人要拜访N个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。TSP问题是一个组合优化问题,该问题如果用穷举的方法解决,解的空间范围是指数级的。是NP完全问题。
模拟退火:
- 采用多种邻域操作的局部搜索local search策略求解;
- 在局部搜索策略的基础上,加入模拟退火simulated annealing策略,并比较两者的效果;
- 要求求得的解不要超过最优值的10%,并能够提供可视化,观察路径的变化和交叉程度。
遗传算法:
- 设计较好的交叉操作,并且引入多种局部搜索操作(可替换通常遗传算法的变异操作)
- 和之前的模拟退火算法(采用相同的局部搜索操作)进行比较
- 得出设计高效遗传算法的一些经验,并比较单点搜索和多点搜索的优缺点。
二、 实验内容
1.算法原理
1.1 局部搜索
搜索领域解之后,若为最优解则采纳,若为劣解一定丢弃。局部搜索容易陷入局部最优解
1.2 模拟退火
模拟退火算法(Simulated Annealing Algorithm)是元启发式搜索算法的其中一种。相比起效率低下的随机搜索算法,元启发式搜索算法借助了演化思想和集群智能思想,对解的分布有规律的复杂问题有良好的效果。
模拟退火法的基本思想是,在系统朝着能量减小的趋势这样一个变化过程中,偶尔允许系统跳到能量较高的状态,以避开局部极小点,最终稳定到全局最小点。模拟退火不是单纯的采用贪心策略,它每获得一个解,对于该解有两种做法:若该解为更优解,则100%采纳;若该解为劣解,以一定的概率采纳该解,也就是说可能丢弃,可能采纳。所以在模拟退火算法的随机搜索过程中,当前的采纳解是时好时坏,呈现出一种不断波动的情况,但在总体的过程中又朝着最优的方向收敛。
获取解一般采用Metropolis准则: \(\left.p=\left\{\begin{matrix}1&if&E(x_{new})<E(x_{old})\\\exp(-\frac{E(x_{new})-E(x_{old})}T)&if&E(x_{new})\geq E(x_{old})\end{matrix}\right.\right.\)
也就是更优解一定采纳,劣解以一定概率采纳。
模拟退火是一个不断迭代的过程,我们通过设定一个迭代次数来模拟时间,迭代次数不能多也不能少,具体是通过实践出来的。如果设置得太小,那么模拟过程还没有收敛就已经结束了;而设置得太大,那么收敛之后的迭代式浪费时间,因为收敛之后已经不会再变了。(收敛就是达到目前的最优解状态)所以经过多次尝试调出一个恰当的迭代次数是非常有必要。
需要调节参数:
1
2
3
4
5
T0 = 1099.0 # 初始温度
T_end = 1e-4 #最终温度
q = 0.911 # 退火系数
L = 1200 # 每个温度时的迭代次数
N = 105 # 城市数量
1.3 遗传算法
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法,遗传算法从任意一个初始化的群体出发,通过随机选择、交叉和变异等遗传操作,使群体一代一代地进化到搜索空间中越来越好的区域,直至抵达最优解。一般的迭代方法容易陷入局部极小的陷阱而出现”死循环”现象,使迭代无法进行。遗传算法很好地克服了这个缺点,是一种全局优化算法。
遗传算法涉及5大要素
-
参数编码:用城市经过顺序作为编码,每一条路径作为遗传算法中一个个体。
-
初始群体设定:随机生成
Population_Size个随机序列 -
适应度函数设计:当前城市经过顺序的总路程的长度的倒数
-
遗传操作设计:包括交叉,变异,选择
-
控制参数设定:
1 2 3 4
Crossover_Probability = 0.85 Mutation_Probability = 0.2 Population_Size = 150 Generations_Time = 4500
2.伪代码
2.1 模拟退火
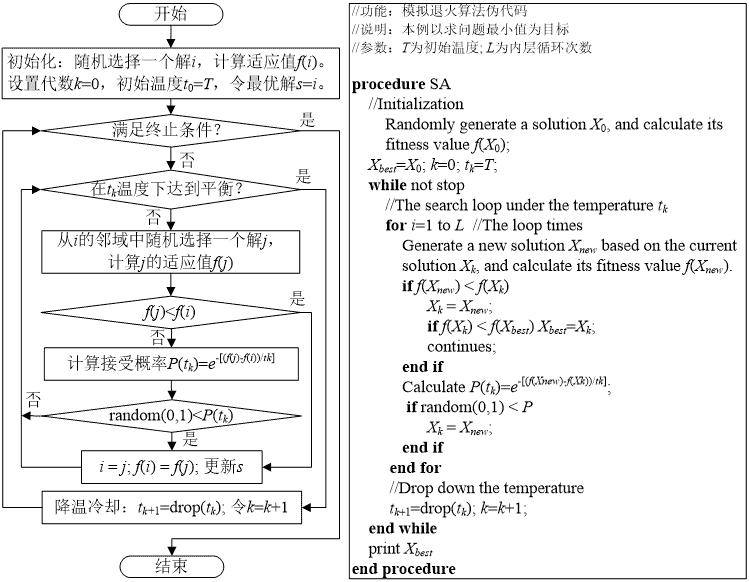
我的算法流程:
- 随机生成一个城市序列作为初始解,比如1、2、… 105,这样的一个序列;设置合适的初温;
- 通过交换两个城市的位置得到序列的领域,作为新解,如果温度为0,则转(6);
- 将新解与最优解比较,如果新解小于最优解,则将新解作为最优解,否则则以Metropolis准则决定是否接受差解为最优解;
- 如果系统处于平衡状态,则转(5),否则接着执行(2);
- 降温,迭代计数器加1,返回(2);
- 输出最优解。
其中,我们给每个城市编号1-N,每一个解对应一个路径序列,代表通过这个路径走遍全部城市。我们评估函数就是这个路径的大小,最终目的就是尽可能找到一个路径长度最小的解。关于达到系统平衡状态,这个我们设置一个内置的循环,整个算法是双重循环,外循环表示退火过程,内循环迭代致使达到一个平衡状态。
2.2 遗传算法
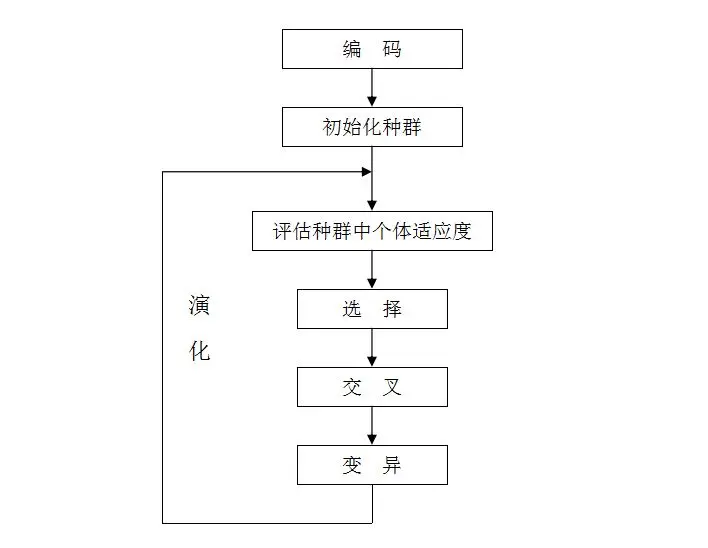
我的算法细节:
初始群体设定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 生成随机解决方案
def generate_random_solution(self):
# 返回一个随机生成的解决方案
path = list(range(self.n))
random.shuffle(path)
return path
# 初始化种群
def initialize_population(self):
# 生成一个包含population_size个随机解决方案的列表
population = []
for i in range(self.population_size):
population.append(self.generate_random_solution())
return population
选择
这里的选择是指经过了交叉,变异后的群组中选择一些优秀的个体
1
2
3
4
5
6
7
8
# 选择操作
def select(self, population):
# 根据适应度函数选择两个个体作为父代进行交叉和变异
fitness_scores = [self.cal_path_len(solution) for solution in population]
# 这里根据概率来选择父代
parent1_index = np.random.choice(len(population), p=fitness_scores / np.sum(fitness_scores))
parent2_index = np.random.choice(len(population), p=fitness_scores / np.sum(fitness_scores))
return population[parent1_index], population[parent2_index]
交叉
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 交叉操作
# 这里采取OX方法
def crossover(self, parent1, parent2):
# 将两个父代交叉产生子代
if random.random() < self.crossover_probability:
# 随机选择两个交叉点
index1 = random.randint(0, self.n - 1)
index2 = random.randint(index1, self.n - 1)
child = [-1] * self.n
for i in range(index1, index2 + 1):
child[i] = parent1[i]
# 将剩下的结点全部按parent2中的相对顺序录入child中
missing_cities = [j for j in parent2 if j not in child]
for i in range(self.n):
if child[i] == -1:
child[i] = missing_cities.pop(0)
return child
else:
return parent1
变异
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 变异操作
def mutate(self, path):
new_path = path.copy()
index1 = random.randint(0, self.n - 1) # 随机生成一个[0, self.n - 1]的序号
index2 = random.randint(0, self.n - 1)
# select = random.randint(0, 1)
select = 1
if select == 0:
new_path[index1], new_path[index2] = new_path[index2], new_path[index1]
else:
index1, index2 = min(index1, index2), max(index1, index2)
for i in range(index1, index2+1):
new_path[i] = path[index1+index2-i]
return new_path
更新
1
2
3
4
5
# 合并父代种群和子代种群,留下适应力最好的generations个
def merge_parent_child(self, parent_population, child_population):
merged = parent_population + child_population
merged.sort(key=self.cal_path_len) # 按照适应值排序
return merged[:self.population_size]
3.关键代码展示(带注释)
3.1 局部搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def LocalSearch_TSP(self):
T = 0
global path
self.read_tsp_data()
path_copy = list(path) # 用于保存原始解
with open("./result/localresult.txt", "w") as outfile:
with open("./result/localresult2.txt", "w") as outfile2:
# 当温度低于结束温度时,退火结束
count_output = 0
count = 0
while count<=LOOP_TIME:
path_copy = list(path) # 复制数组
self.get_new_solution() # 产生新解
fitness1 = self.cal_path_len(path_copy)
fitness2 = self.cal_path_len(path)
df = fitness2 - fitness1
# 如果新解更优,接受新解
if df < 0:
outfile2.write(str(self.cal_path_len(path)) + "\n")
if count % 1000 == 0:
print("当前最优解: ", self.cal_path_len(path))
count_output += 1
# 否则保存旧值
else:
if count % 1000 == 0:
print("最优解无变化,仍为", self.cal_path_len(path_copy))
path = path_copy.copy()
if count % 8000 == 0: # 每隔8000次输出一次路径
for i in range(N):
outfile.write(str(i+1) + "\t" + str(path[i]) + "\n")
count += 1
3.2 模拟退火
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def SA_TSP(self):
T = T0
count = 0 # 记录降温次数
self.read_tsp_data()
global path
path_copy = list(path) # 用于保存原始解
with open("./result/SAresult.txt", "w") as outfile:
with open("./result/SAresult2.txt", "w") as outfile2:
# 当温度低于结束温度时,退火结束
count_output = 0
while T > T_end:
for i in range(L):
path_copy = list(path) # 复制数组
self.get_new_solution() # 产生新解
fitness1 = self.cal_path_len(path_copy)
fitness2 = self.cal_path_len(path)
df = fitness2 - fitness1
# 退火准则:Metropolis准则
if df >= 0:
r = random.random() # 0-1之间随机数,用来决定是否接受新解
# 保留原来的解
if math.exp(-df / T) <= r: #Metroplis准则
path = list(path_copy)
outfile2.write(str(self.cal_path_len(path)) + "\n")
print("当前温度: ", T, " ", "当前最优解: ", self.cal_path_len(path))
count_output += 1
if count % 10 == 0: #每10次保存一次当前解
for i in range(N):
outfile.write(str(i + 1) + "\t" + str(path[i]) + "\n")
T *= q # 降温,q为降温系数
count += 1
return count
3.3 遗传算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def GA_TSP(self):
with open("./result/GAresult.txt", "w") as outfile:
with open("./result/GAresult2.txt", "w") as outfile2:
# # 记录好数据,后面要绘制图像
# 初始化种群
population = self.initialize_population()
# 最佳解决方案
index = np.argmax([self.cal_path_len(solution) for solution in population])
best_path = population[index]
best_length = self.cal_path_len(population[index])
# 迭代多次,直到达到停止条件
for i in range(self.generations):
next_population = []
for _ in range(self.population_size):
# 选择两个父代
parent1, parent2 = self.select(population)
# 通过交叉和变异制造新后代
child = self.crossover(parent1, parent2)
child = self.mutate(child)
next_population.append(child)
population = self.merge_parent_child(population, next_population)
cur_index = np.argmax([self.cal_path_len(solution) for solution in population])
cur_path = population[cur_index]
cur_length = self.cal_path_len(population[cur_index])
if cur_length < best_length:
best_length = cur_length
best_path = cur_path
if i % 10 == 0:
print("迭代次数:"+str(i)+"当前最好距离:"+str(best_length))
outfile2.write(str(best_length) + "\n")
if i % 100 == 0:
for n in range(N):
outfile.write(str(n + 1) + "\t" + str(best_path[n]+1) + "\n")
return best_length, best_path
4.创新点&优化
采用了多种邻域搜索方法相结合的获得邻域解的方法,加快了算法收敛的速度。
三、 实验结果及分析
1.实验结果展示示例(可图可表可文字,尽量可视化)
局部搜索

初始化时:
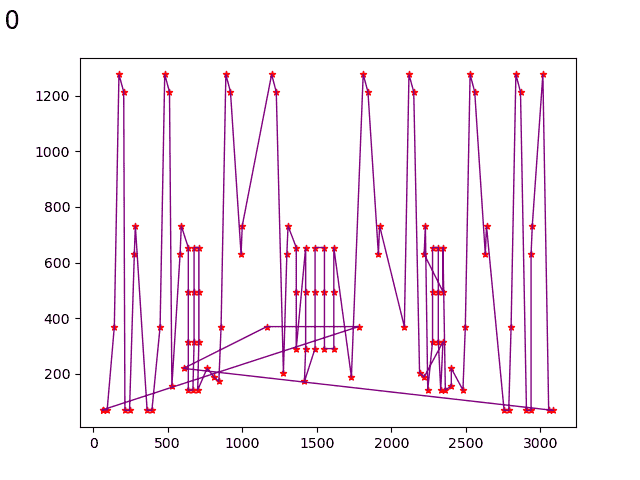
经过局部搜索后:
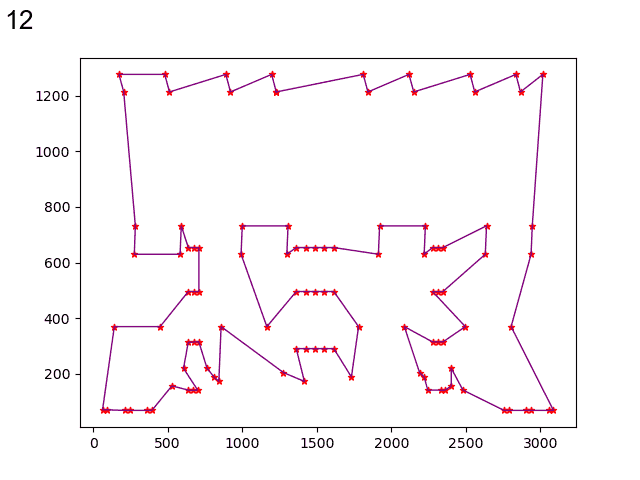
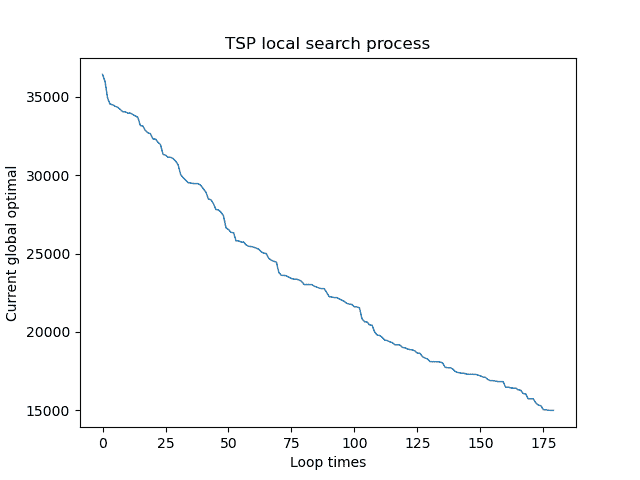
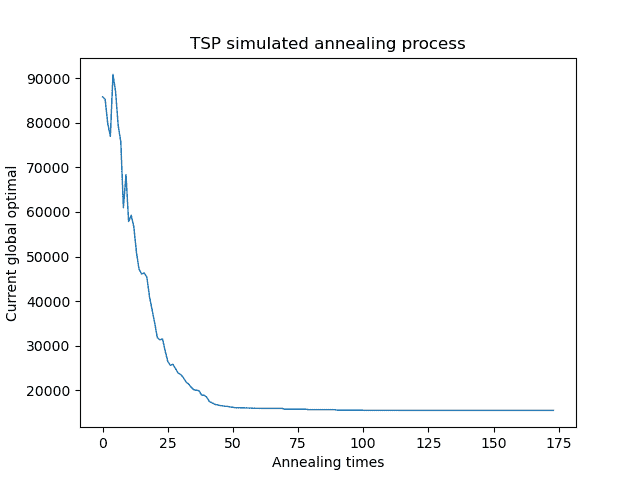
模拟退火
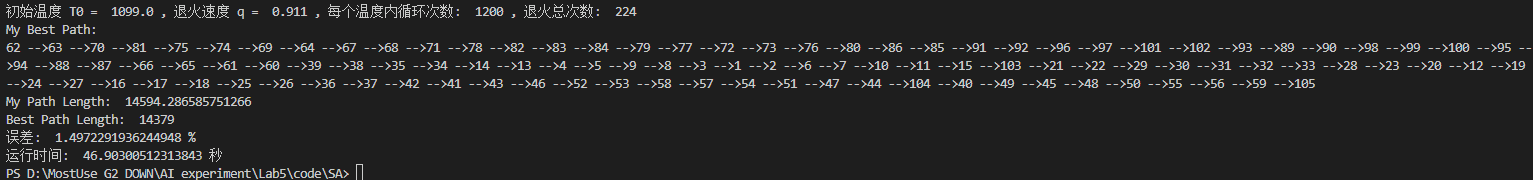
初始化时:
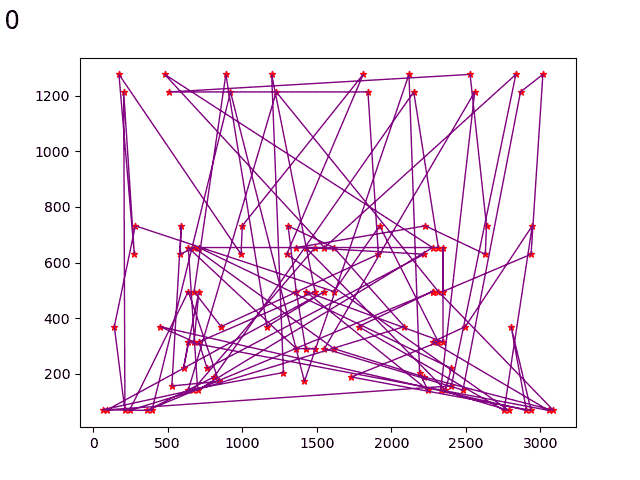
经过模拟退火优化后:
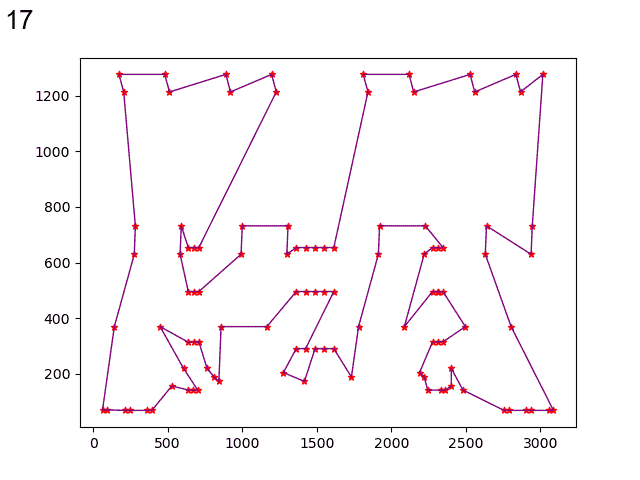
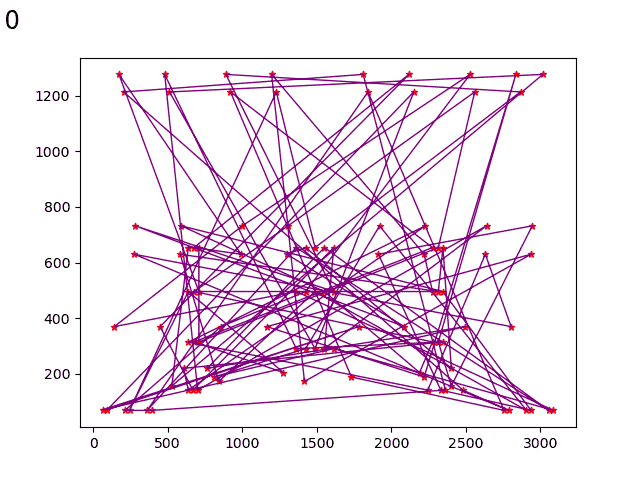
遗传算法

初始化时:
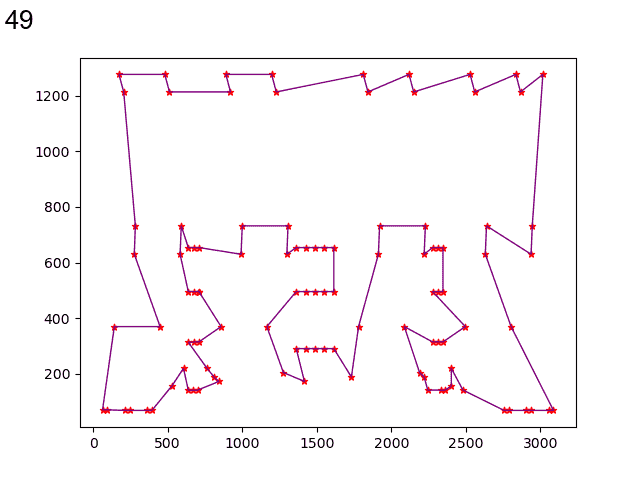
经过遗传算法优化后:
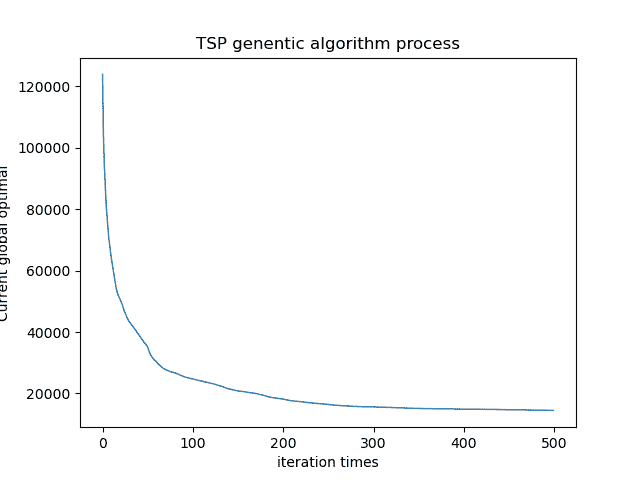
2.评测指标展示及分析(机器学习实验必须有此项,其它可分析运行时间等)
lin105的最优解为14379
局部搜索
| 次数 | 计算所得最优解 | 误差 | 运行时间 |
|---|---|---|---|
| 1 | 15978.56450 | 11.124309790412337 % | 17.59174633 秒 |
| 2 | 16252.56757 | 13.02988788111186 % | 17.62054920 秒 |
| 3 | 16116.58346 | 12.084174566511203 % | 17.11651396 秒 |
| 4 | 15701.01634 | 9.194077078199113 % | 16.90215206 秒 |
| 5 | 15949.56473 | 10.922628381142315 % | 17.21364259 秒 |
平均值:15999.65932 平均值:11.27% 运行时间:17.28892083
模拟退火
| 次数 | 计算所得最优解 | 误差 | 运行时间 |
|---|---|---|---|
| 1 | 15247.19986 | 6.037971129733938 % | 38.52572655 秒 |
| 2 | 14872.56020 | 3.4325071977408443 % | 37.84124875 秒 |
| 3 | 15326.88095 | 6.592120152634738 % | 38.32826924 秒 |
| 4 | 15012.75265 | 4.407487691084154 % | 37.72548437 秒 |
| 5 | 15032.09886 | 4.542032560507192 % | 38.11681938 秒 |
平均值:15098.2985 平均值:5.00% 运行时间:38.10750966
遗传算法
| 次数 | 计算所得最优解 | 误差 | 运行时间 |
|---|---|---|---|
| 1 | 14496.964962364833 | 0.813442954863793 % | 1644.2543394565582 秒 |
| 2 | 14741.413115557607 | 2.520433378938773 % | 2040.2753310203552 秒 |
| 3 | 14555.077347373466 | 1.224007234234342 % | 1880.2312313445667 秒 |
| 4 | 14795.273847891723 | 2.893180398742093 % | 1733.5489983558655 秒 |
| 5 | 14687.347298357982 | 2.143984927837348 % | 1786.3874927348373 秒 |
平均值:14655.21531 平均值:1.92% 运行时间:1816.939479
通过上述实验可以看出,局部搜索算法求出的TSP最优解误差较大,平均误差在11.27%,但是算法的运算时间较少,收敛速度较快。故需要一些不太精确的近似解时,可以利用局部搜索的方法来寻找。
模拟退火比局部搜索能找到更加精确的解,误差在5%到10%之间,但是使用的时间会更多,因为模拟退火在每一个温度都进行了相当多次的局部搜索,通过概率接受差解来跳出局部最优,达到更高的精度。
摸拟退火算法是基于随机搜索的,即在解的空间中展开随机搜索的。当问题的空间很大,而可行解比较多,并且对解的精度要求不高时,随机搜索是很有效的解决办法,因为其他的做法在这个时候时空效率不能让人满意。而借助演化思想和群集智能思想改进过的随机算法更是对解的分布有规律的复杂问题有良好的效果。
通过遗传算法解决TSP问题得到解的精度能把误差控制在5%以内,算法的速度大概在1816s左右。
与局部搜索算法对比:
- 局部搜索收敛速度较快,遗传算法收敛较慢
- 局部搜索的误差在10%左右,遗传算法可以做到3%的最小误差
- 局部搜索容易陷入局部最优,遗传算法可以跳出局部最优,查找全局最优解
与模拟退火算法对比:
- 模拟退火的误差维持在5%左右,稍差于遗传算法
- 模拟退火是采用单个个体进行优化,遗传算法是一种群体性算法。
- 模拟退火与遗传算法都对初解有一定的依赖性,好的初解有利于最终解
- 遗传算法可以采用并行计算来加快算法运行
算法能找出误差值维持在3%到5%的TSP路径,能较好的解决TSP问题。
缺点是算法在3000代左右,已经能找到误差小于10%的解,但在寻找更优解的时候,花费的时间成本确是大于之前花费找到10%的解时间。这个可以通过调整变异率来解决这一问题,当我的变异率较低的时候,我的遗传算法收敛速度很快但找到的值误差在6%以上,为了发挥其潜能,我提高了一点变异率,所以导致算法跑的速度变慢,邻域搜索更多。
四、 思考
比较单点搜索和多点搜索的优缺点:
- 单点搜索,以模拟退火为例子。模拟退火算法虽具有摆脱局部最优解的能力,能够以随机搜索技术从概率的意义上找出目标函数的全局最小点。但是,由于模拟退火算法对整个搜索空间的状况了解不多,不便于使搜索过程进入最有希望的搜索区域,使得模拟退火算法的运算效率不高。模拟退火算法对参数(如初始温度)的依赖性较强,且进化速度慢。
- 多点搜索,以遗传算法为例子。遗传算法具有良好的全局搜索能力,可以快速地将解空间中的全体解搜索出,而不会陷入局部最优解的快速下降陷阱;并且利用它的内在并行性,可以方便地进行分布式计算,加快求解速度。但是遗传算法的局部搜索能力较差,导致单纯的遗传算法比较费时,在进化后期搜索效率较低。在实际应用中,遗传算法容易产生早熟收敛的问题。采用何种选择方法既要使优良个体得以保留,又要维持群体的多样性,一直是遗传算法中较难解决的问题。