使用A* 与IDA* 算法解决15-Puzzle问题
一、 实验题目
使用A* 与IDA* 算法解决15-Puzzle问题
启发式搜索与盲⽬搜索或者⽆信息搜索最⼤的区别就在于启发式搜索采⽤了启发信息来引导整个搜索的过程,能够 减少搜索的范围,降低求解问题的复杂度。这⾥的启发信息主要由估价函数组成,估价函数f(x)由两部分组成,从 初始结点到当前结点n所付出的实际代价g(n)和从当前结点n到⽬标结点的最优路径的代价估计值h(n),即:
f(n)=g(n)+h(n)
二、 实验内容
15puzzle 问题:寻找15 puzzle 的一个解相对容易,但寻找 最优解 是一个 NP 困难 问题。15-Puzzle 的最优解至多有 80 步
1.算法原理
1.1 A*算法
A* 算法是一种常用于寻路问题的启发式搜索算法。它通过启发式函数(heuristic function)来评估每个节点的优先级,以确定下一个要扩展的节点。
A* 算法的启发式函数可以根据具体情况选择不同的实现方式,如曼哈顿距离、线性冲突等。A*算法可以保证找到最短路径,但如果启发式函数不准确,则可能会导致找到的路径不是最优路径。
A* 算法通过估算每个节点到目标节点的距离,来寻找最短路径。在搜索过程中,A* 算法维护两个值:节点的实际代价g和启发式估计代价h。g代表从起点到当前节点的实际代价,h代表从当前节点到目标节点的估计代价。A* 算法使用这两个代价值之和f来选择下一个要搜索的节点,并且在每次搜索中选择最优的节点以保证最短路径被找到。A*算法的搜索过程中需要维护一个开放列表和一个关闭列表。开放列表用于存储待搜索的节点,关闭列表用于存储已经搜索过的节点。在每一次搜索中,从开放列表中选取代价最小的节点,将其作为当前节点,并将其从开放列表中移除,加入到关闭列表中。然后,根据当前节点的邻居节点计算出它们的代价值,将它们加入到开放列表中。如果目标节点被加入到开放列表中,搜索结束,路径被找到。
我的算法设计:
-
final_state 表示目标状态,init_state 表示初始状态。dir_x 和 dir_y 表示向四个方向的偏移量,man_parameter 是曼哈顿距离的乘数,可以调整算法的搜索效率。open 和 close 分别表示开放列表和关闭列表,path 存储路径。
-
Node 类表示状态节点,它包含了状态的当前代价 gn、估计代价 hn、总代价 fn、状态的值 state 和父节点 parent。在比较两个状态节点大小时,根据 fn 值大小进行比较,如果 fn 相等,则比较 hn 值。
-
启发式函数上:Manhattan 函数计算曼哈顿距离,并乘以 man_parameter。Misplaced 函数计算不在目标位置上的数字数量。LinearConflict 函数计算行列冲突数。
在搜索过程中,首先将初始状态加入Open表中。然后进行循环,直到找到目标状态或者Open表为空。在每次循环中,选择Open表中 f(n) 值最小的状态进行扩展,并将其从Open表中删除,并加入Close表中。对于当前状态的每个邻居状态,如果它已经在Close表中,则跳过,否则将其加入Open表中。对于Open表中已经存在的状态,如果新的 gn 值更小,则更新该状态的 gn、fn 和 parent。当找到目标状态时,从目标状态开始反向遍历父节点即可得到路径。
A*算法缺点:该算法一般要使用大量的空间用于存储已搜索过的中间状态,防止重复搜索。随着样例变复杂将会爆内存。
1.2 IDA*算法
IDA* 算法是一种启发式搜索算法,IDA*算法的原理是基于深度优先搜索(DFS)和迭代加深搜索(IDS)的思想,结合了启发函数(h)来估计距离目标状态的代价。启发函数可以选择不同的度量方式,例如曼哈顿距离、错位数等。
IDA*算法在搜索过程中会遍历状态空间中的所有节点,每个节点都会被评估并与阈值进行比较。如果节点的成本低于当前阈值,那么该节点就会被扩展。如果节点的成本超过当前阈值,则会剪枝,回溯到上一个节点并重新搜索。
IDA* 算法的优点是它只需要存储当前路径的节点,而不是整个状态空间。这意味着它可以处理非常大的状态空间,而不会占用太多的内存。此外,IDA*算法是一种完备的算法,可以保证找到最优解,同时还可以在运行时动态地调整搜索深度,从而更快地找到解决方案。
我的算法设计:
- IDA_star(start):主函数,接收初始状态作为输入,并返回找到的路径。该函数采用迭代加深搜索的方式实现IDA*算法,其中bound变量表示当前的最大搜索深度。在每轮搜索中,函数search从初始状态开始搜索,直到找到目标状态或达到搜索深度的限制。如果找到了目标状态,则返回找到的路径。否则,将搜索深度扩大到下一层,并继续搜索。
- search(cur_state, g, bound, path):递归函数,用于搜索当前状态的相邻状态。其中cur_state表示当前状态,g表示到达当前状态所需的步数,bound表示当前的最大搜索深度,path表示搜索路径。该函数首先计算当前状态的f值(即g值加上曼哈顿距离),如果f值大于bound,则返回f值;如果当前状态已经是目标状态,则返回-1。否则,对当前状态的所有相邻状态进行搜索,并记录最小的搜索深度,最后返回该值。
- get_neighbors(cur_state):辅助函数,用于返回当前状态的所有相邻状态。该函数首先找到当前状态中数字0的位置,然后尝试将其和上下左右四个方向上的数字进行交换。如果新的状态在搜索路径中没有出现过,则将其加入到相邻状态列表中。
- Manhattan(state):启发式函数,用于计算当前状态和目标状态之间的曼哈顿距离。曼哈顿距离是指当前状态中每个数字到其目标位置的曼哈顿距离之和。其中aim_x和aim_y表示数字n的目标位置。
基于迭代加深的A算法 (IDA) 是A* 算法的优化,两者虽然时间复杂度相似,但IDA* 采用深度优先搜索(DFS)的策略,使得程序对内存空间的占用由指数级增长降为线性增长 (程序使用内存与搜索深度呈线性关系),大大减少了内存的使用。总的来说,IDA*会根据一个启发式方法(这里我们采用曼哈顿距离),算出所谓的“启发式评价” (即预估采用最优方案达到最终状态所需要的步数),然后开始循环一定数量的DFS。每个DFS不仅会记录其已经搜索的深度(即距离初始状态已移动的步数),还会在每移动一步到达一个新的状态时,对该状态重新计算“启发式评价”得到属于该状态的评价步数。如果我们采用的是可采纳的启发式评价算法,那么:
已搜索的深度 + 当前启发式评价步数 = 到达理想状态所需的最小步数
若这个和大于最初的启发式评价,我们便可以认为这个搜索没有必要再进行下去了,因为这个搜索路径的所需的最小步数已经高于我们预估的最佳方案了。所以,一个DFS终止的条件有二,一是它的已搜索的深度与当前启发式评价步数之和大于预估的步数了,二是它搜索到了最终状态,即找到了最优路径。
当然,如上所述,预估的启发式评价通常在最佳步数本身就比较少时比较准确,当需要完成的步数很多时,启发式评价得到的预估步数往往会比真实值小上一些,这时候在预估步数的限制下,所有DFS都不会达到最终状态。所以在所有DFS都进行完成但没有最终状态出现的时候,我们就需要更新总的预估步数,将步数增加使得DFS可以达到更深的深度。这里更新预估步数值可以采用取之前一轮DFS中,所有超出预估步数的和 (已搜索的深度+当前启发式评价步数) 里面,最小的那个值,这样可以确保新的一轮DFS只会往更深的一层而不是多层去搜索。更新预估步数值后,即可开始新一轮的DFS,如此往复直到搜索由于找到最终状态而停止。
(以上这段分析对于理解IDA*算法很重要)
1.3 启发式函数设计
启发式函数需要满⾜以下两种性质: 1.可采纳的(admissible)
2.单调的(consistent)
启发式函数的准确性直接影响搜索算法的性能。由于搜索算法的目标是找到最优解,因此启发式函数应该尽可能接近实际距离。当估价函数低估实际距离时,搜索算法会产生过多的扩展节点,导致算法运行时间增加。相反,当估价函数高估实际距离时,搜索算法可能会错过更优解,导致算法不能找到最优解。
因此,分情况分析估价值和真实值的差距非常重要,可以设计更准确的启发式函数。使用多种启发式函数来评估问题可能是一个好的策略,==可以在算法性能和搜索时间之间找到一个平衡点。==
| h(n) 的值 | 描述 | 性能变化 |
|---|---|---|
| h(n) = 0 | 只有g(n)起作用,退化为Dijkstra算法 | 保证找到最短路径,但速度极慢 |
| h(n) <= h*(n) | 保证能找到最短路径,速度可能较慢 | |
| h(n) = h*(n) | 只遵循最佳路径不会扩展其它节点 | 运行速度快并且能找到最短路径 |
| h(n) > h*(n) | 不能保证找到最短路径,但是速度将加快 |
第一个启发式函数,曼哈顿距离,计算每个方块到达其最终位置所需的总步数。其方法是将当前方块的位置与其目标位置之间的水平和垂直距离相加,得到曼哈顿距离。然后将所有方块的曼哈顿距离相加,作为估计距离。这个估计距离可以作为搜索算法中的估价函数,帮助算法找到最优解。
第二个启发式函数,错位数,计算当前状态下与目标状态相比不在其正确位置上的方块数量。这个估计距离忽略了方块之间的距离,因此会低估实际距离。但是,由于它很容易计算,可以作为一种较简单的估计函数,用于加速搜索过程。
第三个启发式函数,线性冲突,考虑了方块在其目标位置所需的行和列上的顺序关系。当两个方块在同一行或同一列上,且它们的目标位置在它们之间时,它们会发生线性冲突。这意味着它们必须相互移动才能达到其目标位置,从而增加了移动的步数。通过计算每行和每列的线性冲突数,可以将其添加到曼哈顿距离中,得到更准确的估计距离。
2.伪代码
2.1 A*算法
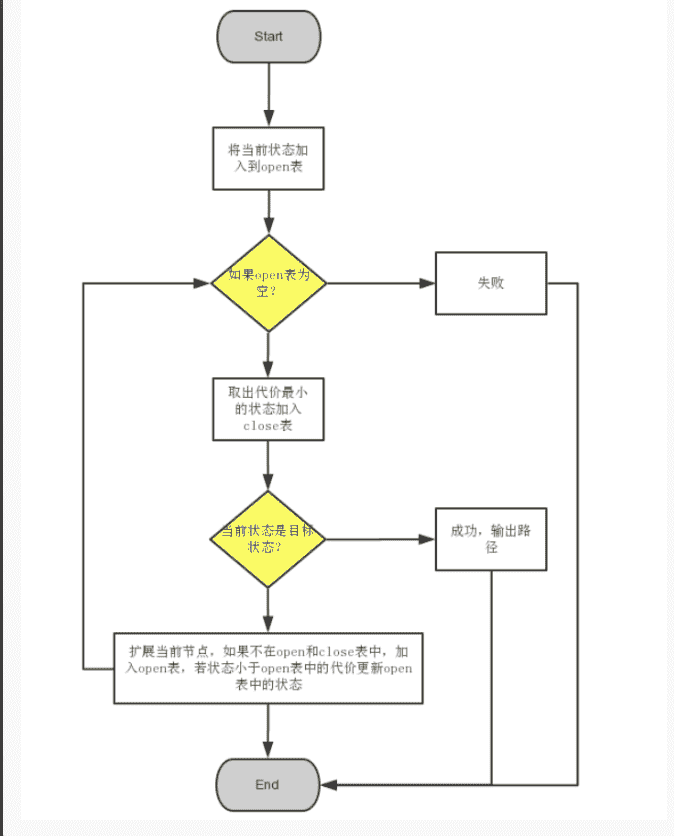
以下是A*算法的步骤:
-
初始化:将起点加入Open表,并将其启发式函数值(估计到终点的距离)和g值相加设置为f值。
-
进行循环:如果开放列表不为空,则执行以下步骤:
a. 选择开放列表中f值最小的节点,并将其从开放列表中移除。
b. 如果该节点是终点,则返回解决方案。
c. 扩展该节点:对于所有邻接节点,计算其启发式函数值和g值(从起点到该节点的实际距离),并计算其f值。如果邻接节点已经在Open表或Close表中,则更新其f值和父节点指针,如果未在列表中,则将其加入Open表。
d. 将该节点加入Close表。
-
如果开放列表为空且没有找到解决方案,则问题无解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
初始化open表和close表,path表
A_star(start) 传入初始状态
将起点加入open_set中,并设置优先级为0(优先级最高)
if open不为空,选open表中fn最小的节点cur_node:
if cur_node的状态与目标状态一样:
从终点开始逐步追踪parent节点,一直达到起点
return path 返回找到的结果路径,算法结束
if cur_node 不是目标状态:
将节点cur_node从open表中删除,并加入close表中;
for cur_node所有的邻近节点:
if 邻近节点m在close表中:
continute 跳过,选取下一个邻近节点
if 邻近节点m也不在open表中:
设置节点m的parent为节点cur_node
计算节点m的fn
将节点m加入open表中
2.2 A*优化
用迪杰斯特拉算法的思想,更新gn的值,使得答案路径上的每个节点的gn都是最小的(离初始节点最近)
1
if not hash_value in close.keys() or close[hash_value] > new_gn:
在close表中增加一点信息,提高速度。
2.3 IDA*算法
IDA*算法的步骤如下:
- 选择一个合适的启发函数h,并设定初始限制值为h(s),其中s为初始状态。
- 从初始状态s开始进行DFS,对于每个扩展节点n,计算f(n) = g(n) + h(n),其中g(n)为从s到n的实际代价。如果f(n)超过当前限制值,则剪枝该节点及其子节点,并记录最小超过限制值的f(n)作为新限制值,然后回溯到上一个节点重新搜索。
- 如果在DFS过程中找到目标状态,则返回成功;如果DFS结束后没有找到目标状态,则用新限制值重复步骤2,直到找到目标状态或者新限制值无穷大为止。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
IDA_star(strat)
bound = h(strat)
while true
t = search(strat, 0, bound)
if t == FOUND then return FOUND
if t == ∞ then return NOT_FOUND
bound = t
search(cur_state, g, bound)
f = g + h(cur_state)
if f > bound then return f
if node is goal then return FOUND
min = ∞
for child in expand(cur_state) do
t = search(child, g + cost(cur_state, child), bound)
if t == FOUND then return FOUND
if t < min then min = t
end for
return min
3.关键代码展示(带注释)
启发式函数如下,A*算法和IDA *算法用的启发式函数一致:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def Manhattan(state):
manhattan_dist = 0
for i in range(4):
for j in range(4):
if state[i][j] == 0 or state[i][j] == final_state[i][j]:
continue
else:
aim_x = (state[i][j] - 1) // 4
aim_y = (state[i][j] - 1) % 4
manhattan_dist += (abs(aim_x - i) + abs(aim_y - j))
return manhattan_dist*man_parameter #1.125
def Misplaced(state):
sum = 0
for i in range(4):
for j in range(4):
if state[i][j] == 0:
continue
if state[i][j] != final_state[i][j]:
sum += 1
return sum
def LinearConflict(state):
linear_conflict_count = 0
# 计算每行和每列的冲突数
for i in range(4):
row_conflicts = 0
col_conflicts = 0
for j in range(4):
if state[i][j] == 0:
continue
aim_x = (state[i][j] - 1) // 4
aim_y = (state[i][j] - 1) % 4
if aim_x == i: #当前
for k in range(j+1, 4):
if state[i][k] == 0:
continue
if aim_x == i and state[i][j] > state[i][k]:
row_conflicts += 1
if aim_y == j:
for k in range(i+1, 4):
if state[k][j] == 0:
continue
if aim_y==j and state[i][j] > state[k][j]:
col_conflicts += 1
linear_conflict_count += row_conflicts + col_conflicts
# 返回曼哈顿距离和冲突数的和
return Manhattan(state) + 2 * linear_conflict_count
3.1 A*算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def A_star(start):
root = Node(0, 0, start, None) # gn, hn, state, parent
open.append(root)
hash_value=hash(str(start))
close.add(hash_value)
node_num=0
while len(open) != 0:
cur_node = heapq.heappop(open)
node_num += 1
if cur_node.state == final_state:
return add_path(cur_node),node_num
for i in range(4):
for j in range(4):
if cur_node.state[i][j] != 0:
continue
for d in range(4):
new_x = i + dir_x[d]
new_y = j + dir_y[d]
if 0 <= new_x <= 3 and 0 <= new_y <= 3:
state = copy.deepcopy(cur_node.state)
temp=state[i][j]
state[i][j] = state[new_x][new_y]
state[new_x][new_y] = temp
hash_value = hash(str(state))
if hash_value in close:
continue
close.add(hash_value)
hn=Manhattan(state)
# hn=Misplaced(state)
# hn=LinearConflict(state)
# hn=BFS(state)
# hn=InversionDistance(state)
new_node = Node(cur_node.gn+1, hn, state, cur_node)
heapq.heappush(open, new_node)
return [],0
3.2 A*优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def A_star(start):
root = Node(0, 0, start, None) # gn, hn, state, parent
open.append(root)
hash_value=hash(str(start))
# close.add(hash_value)
close[hash]=0
node_num=0
while len(open) != 0:
cur_node = heapq.heappop(open)
node_num += 1
if cur_node.state == final_state:
return add_path(cur_node),node_num
for i in range(4):
for j in range(4):
if cur_node.state[i][j] != 0:
continue
for d in range(4):
new_x = i + dir_x[d]
new_y = j + dir_y[d]
if 0 <= new_x <= 3 and 0 <= new_y <= 3:
state = copy.deepcopy(cur_node.state)
state[i][j] = state[new_x][new_y]
state[new_x][new_y] = 0
hash_value = hash(str(state))
new_gn=cur_node.gn+1
if not hash_value in close.keys() or close[hash_value] > new_gn:
# close.add(hash_value)
close[hash_value] = new_gn
# hn=Manhattan(state)
# hn=Misplaced(state)
# hn=LinearConflict(state)
hn=h_fun(state)
# hn=InversionDistance(state)
new_node = Node(cur_node.gn+1, hn, state, cur_node)
heapq.heappush(open, new_node)
return [],0
3.3 IDA*算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def IDA_star(start):
# 估价函数用于计算当前状态和目标状态之间的距离
# bound = Manhattan(start)
# bound = Misplaced(start)
bound = LinearConflict(start)
path=[]
path.append(start)
while True:
# t = search(path[-1], 0, bound, path) #与下面一个等价
t = search(start, 0, bound, path) #要是回到这里,说明深度设定太浅,当前深度下没有找到解决方案,要增加深度限制(即增加bound),直到找到解决方案为止
if t == -1: #找到目标状态
return path # 返回路径
if t == float("inf"):
return None # 没有解决方案
bound = t #t是上一个迭代中找到的路径的最小成本,用它代表下一个迭代的新边界
辅助函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def search(cur_state, g, bound, path): #DFS,每次记录最小深度
f = g + Manhattan(cur_state)
#递归结束条件
if f > bound:
return f
if cur_state == final_state:
return -1 # 找到目标状态
min_bound = float("inf")
for neighbor in get_neighbors(cur_state):
if neighbor not in path:
path.append(neighbor)#加入到路径中避免重复访问
t = search(neighbor, g + 1, bound, path)
if t == -1:
return -1
if t < min_bound:
min_bound = t
path.pop()#删掉本次走过节点,因为能到这说明t!=-1,即本次向下探索超过了bound还没有找到目标状态
return min_bound
def get_neighbors(cur_state): #用于返回当前状态的所有相邻状态
neighbors = []
for i in range(4):
for j in range(4):
if cur_state[i][j] != 0:
continue
for d in range(4):
new_x = i + dir_x[d]
new_y = j + dir_y[d]
if 0 <= new_x <= 3 and 0 <= new_y <= 3:
new_state = copy.deepcopy(cur_state)
temp=new_state[i][j]
new_state[i][j] = new_state[new_x][new_y]
new_state[new_x][new_y] = temp
neighbors.append(new_state)
return neighbors
4.创新点&优化(如果有)
-
在A*算法中,用了迪杰斯特拉思想加快速度,路径更短。
-
不仅用了曼哈顿距离和错位数这两个启发式函数,还用了线性冲突这一启发式函数,同时给曼哈顿距离乘一个参数man_parameter,虽然这样的启发式函数不满足可接纳性(不一定是最短路径),但是可以调节程序运行的速度和找到步数的大小。man_parameter越大,那么找到最终结果速度越快,拓展的节点数越少,但是最终步数也越大。但man_parameter不是越大越好.
三、 实验结果及分析
1.实验结果展示示例(可图可表可文字,尽量可视化)
A*算法输出格式为(以样例一为例):
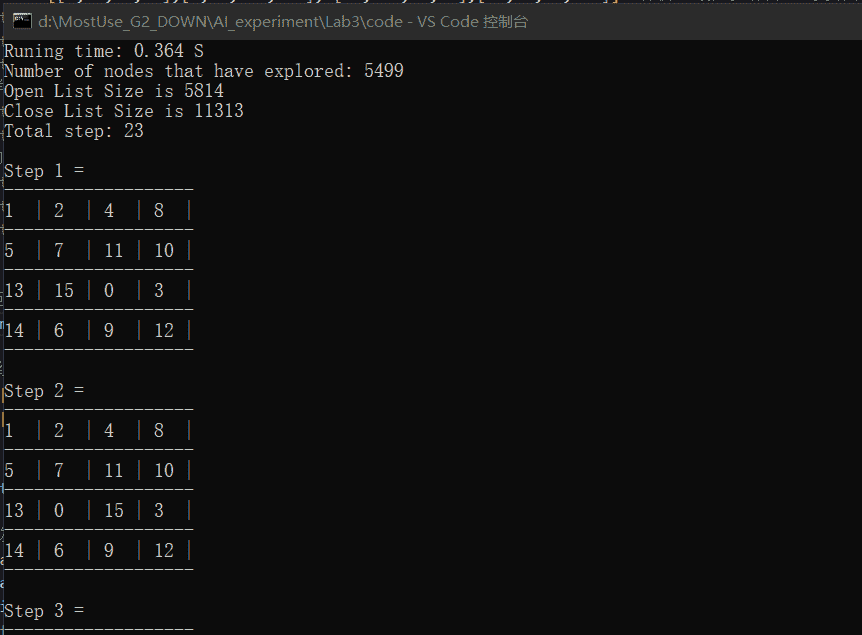
IDA*算法输出格式为(以样例一为例):
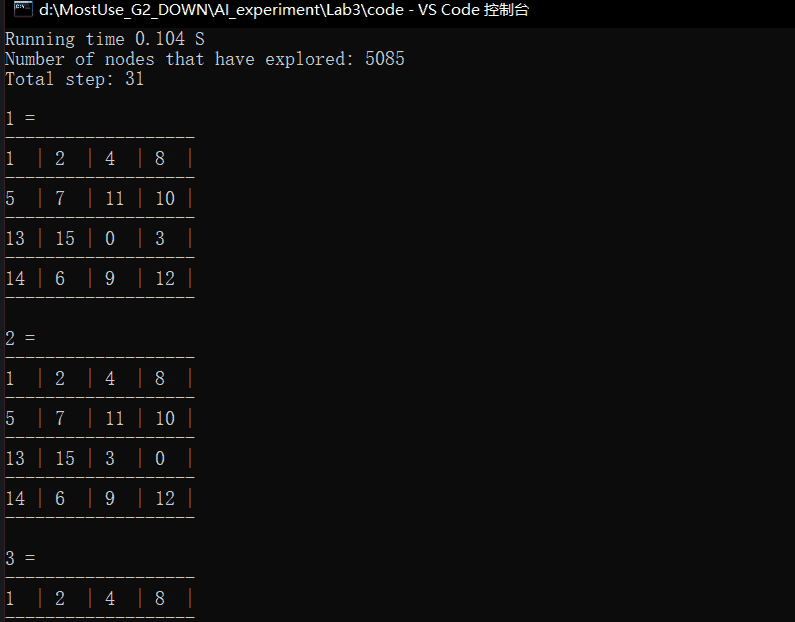
1.1 A*算法
曼哈顿距离
| 样例 | 成功所用步数 | 扩展节点数 | 所用时间 |
|---|---|---|---|
| 1 | 22 | 91 | 0.004 |
| 2 | 15 | 16 | 0.001 |
| 3 | 53 | 4474335 | 612.969 |
| 4 | fail | fail | fail |
| 5 | fail | fail | fail |
| 6 | fail | fail | fail |
曼哈顿距离*man_parameter
| 样例 | 成功所用步数 | 扩展节点数 | 所用时间 |
|---|---|---|---|
| 1 | 26(2) | 326 | 0.005 |
| 2 | 15(2) | 16 | 0.001 |
| 3 | 61(2) | 2692 | 0.122 |
| 4 | 60(2) | 23191 | 1.165 |
| 5 | 64(2) | 15293 | 6.461 |
| 6 | 74(2) | 125425 | 12.976 |
| 6 | 68(1.5) | 293044 | 16.484 |
| 6 | 92(5) | 18862 | 1.866 |
| 6 | 114(10) | 6588 | 0.638 |
| 6 | 146(100) | 3006 | 0.150 |
| 6 | 146(1000) | 3006 | 0.144 |
多次测试后可知man_parameter超过36以后,成功步数稳定在147
错位数:
| 样例 | 成功所用步数 | 扩展节点数 | 所用时间 |
|---|---|---|---|
| 1 | 22 | 5499 | 0.366 |
| 2 | 15 | 36 | 0.003 |
| 3 | fail | fail | fail |
| 4 | fail | fail | fail |
| 5 | fail | fail | fail |
| 6 | fail | fail | fail |
线性冲突加曼哈顿
| 样例 | 成功所用步数 | 扩展节点数 | 所用时间 |
|---|---|---|---|
| 1 | 24 | 87 | 0.004 |
| 2 | 15 | 27 | 0.002 |
| 3 | 53(曼哈顿*1.5) | 17922 | 1.209 |
| 3 | 53 | 1664959 | 160.302 |
| 4 | 58(曼哈顿*1.5) | 71646 | 5.082 |
| 4 | 56 | 1047055 | 94.582 |
| 5 | 66(曼哈顿*1.5) | 11833 | 0.790 |
| 5 | 58 | 2611496 | 310.030 |
| 6 | 74(曼哈顿*1.5) | 486694 | 35.193 |
| 6 | 68 | 6795358 | 566.756 |
1.2 优化后A*
线性冲突加曼哈顿
| 样例 | 成功所用步数 | 扩展节点数 | 所用时间 |
|---|---|---|---|
| 1 | 21 | 53 | 0.018 |
| 2 | 15 | 20 | 0.0001 |
| 3 | 49 | 30661 | 4.920 |
| 4 | 48 | 116222 | 19.000 |
| 5 | 58 | 1311496 | 130.665 |
| 6 | 64 | 2060502 | 220.150 |
1.3 IDA*算法
曼哈顿距离
| 样例 | 成功所用步数 | 扩展节点数 | 所用时间 |
|---|---|---|---|
| 1 | 22 | 171 | 0.005 |
| 2 | 15 | 24 | 0.001 |
| 3 | fail | fail | fail |
| 4 | fail | fail | fail |
| 5 | fail | fail | fail |
| 6 | fail | fail | fail |
曼哈顿距离*man_parameter
| 样例 | 成功所用步数 | 扩展节点数 | 所用时间 |
|---|---|---|---|
| 1 | 34(2) | 1529 | 0.043 |
| 2 | 19(2) | 75 | 0.003 |
| 3 | 63(2) | 87556 | 2.364 |
| 4 | 58(2) | 97033 | 2.612 |
| 5 | 62(2) | 362476 | 9.789 |
| 6 | 82(2) | 810686 | 23.203 |
| 6 | fail(1.5) | fail | fail |
| 6 | 126(3) | 77345 | 1.919 |
| 6 | 82(4) | 3234 | 0.206 |
| 6 | 192(5) | 4344 | 0.211 |
| 6 | 374(10) | 21534 | 1.292 |
错位数:
| 样例 | 成功所用步数 | 扩展节点数 | 所用时间 |
|---|---|---|---|
| 1 | 22 | 172 | 0.005 |
| 2 | 15 | 25 | 0.001 |
| 3 | fail | fail | fail |
| 4 | fail | fail | fail |
| 5 | fail | fail | fail |
| 6 | fail | fail | fail |
线性冲突加曼哈顿
| 样例 | 成功所用步数 | 扩展节点数 | 所用时间 |
|---|---|---|---|
| 1 | 30 | 5085 | 0.136 |
| 2 | 23 | 62 | 0.003 |
| 3 | 55(曼哈顿*1.5) | 56533 | 1.459 |
| 4 | 54(曼哈顿*1.5) | 50099 | 1.255 |
| 5 | 59(曼哈顿*1.5) | 22864576 | 485.188 |
| 6 | 68(曼哈顿*1.5) | 2513867 | 65.379 |
2.评测指标展示及分析(机器学习实验必须有此项,其它可分析运行时间等)
A* 算法的时间复杂度是O(b^d),其中b是每个节点的平均分支数,d是从起点到终点的最短路径长度。
A*算法的空间复杂度是O(b^d),其中b是每个节点的平均分支数,d是从起点到终点的最短路径长度。
IDA*算法的时间复杂度是O(b^d),其中b是每个节点的平均分支数,d是从起点到终点的最短路径长度。
IDA*算法的空间复杂度是O(d),其中d是从起点到终点的最短路径长度。
由上述数据可以看出,曼哈顿距离、错位数、线性冲突加曼哈顿距离这三个启发式函数中最好的是线性冲突加曼哈顿距离,可以在满足可采纳的基础上比较快的计算出最短路径。
同时,优化后的A*算法可以在满足可接纳性前提下比较快的计算出最短路径(路径是几个算法中最短的):
| 样例 | 成功所用步数 |
|---|---|
| 1 | 21 |
| 2 | 15 |
| 3 | 49 |
| 4 | 48 |
| 5 | 58 |
| 6 | 64 |
从以上A* 与IDA* 在深度为40的搜索树的表现情况来看, A* 的搜索效率⼤于IDA* ,此外,从扩展的结点个数来看, IDA* 扩展的结点数更多,这跟IDA* 本身搜索的⽅式有关。 由于A* 需要保存扩展过的结点,因此内存消耗远⼤于 IDA* ,⾄此,可以猜测IDA* 在深度更⼤的搜索问题上表现会⽐A* 更优, A* 需要使⽤复杂度logn优先队列进⾏排 序,可想⽽知当待扩展的结点数⽬剧增的时候,就需要对⼤量的结点进⾏排序,存储开销会⾮常⼤
- 曼哈顿距离启发式函数
它的优点是计算简单且易于实现,但它的缺点是低估了实际距离。
例如,在某些情况下,一个拼图块在最终状态中需要经过多次移动才能到达目标位置。然而,曼哈顿距离只计算了该块当前位置和目标位置之间的距离,而没有考虑到必须经过的额外步骤。这将导致算法低估了实际距离,导致算法搜索更多的节点来找到解决方案。
- 错位块启发式函数
错位块启发式函数计算当前状态中不在其目标位置的块数。虽然它的计算方式很简单,但它也有缺点,即它可能过度关注细节而忽略大局。
例如,在某些情况下,拼图块可能在错误的位置,但是如果它在错误的位置上,它仍然可以在少数移动后到达目标位置。在这种情况下,错位块启发式函数会高估实际距离,导致算法搜索更多的节点来找到解决方案。
- 线性冲突启发式函数
它计算曼哈顿距离和每行和每列中线性冲突的总数之和。尽管线性冲突启发式函数计算相对复杂,但它可以更准确地估计实际距离。这是因为它不仅考虑了曼哈顿距离,还考虑了必须经过的额外步骤。这将导致算法能够更快地找到解决方案。
四、 参考资料
2. Blog: Solving the 15 Puzzle
5.虽然没有参考这一份资料,但是这一篇blog有很多优化15puzzle问题的方法