Computer-Organization NOTES

Chapter3-2-3 浮点数及其运算

Posted by LvKouKou on October 18, 2022

3-2-3 浮点数及其运算

参考文章：

1

https://blog.csdn.net/weixin_58165485/article/details/123235367?ops_request_misc=&request_id=&biz_id=102&utm_term=%E4%BA%8C%E8%BF%9B%E5%88%B6%E6%95%B0%E8%88%8D%E5%85%A5%E7%9A%84%E5%81%B6%E6%95%B0%E6%B3%95%E5%88%99&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-1-123235367.142^v56^new_blog_pos_by_title,201^v3^control_1&spm=1018.2226.3001.4187

n bits 我们可以表示数的范围? Unsigned:0-2n-1 Signed: -2 n-1-2n-1 - 1

浮点数相关笔记在

## 浮点表示

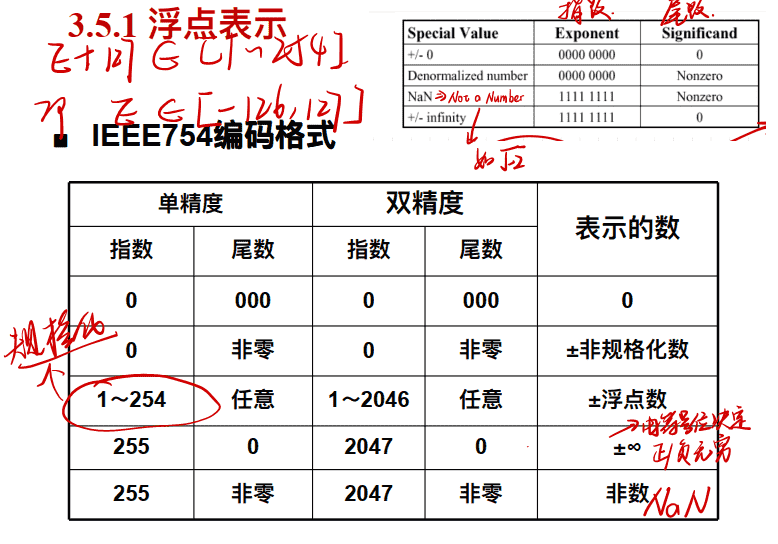
image-20221016232019476

规格化的值

当阶码域不全为0并且不全为1时，表示该数值为规格化的值

对于规格化的值，在得到s, E, M之后还需要进行一些处理才能放进内存：

✨规则1：

前面已经提到，E是阶码并且要可以表示负值，存放在exp字段，但是E在标准中为无符号数，这说明它不能表示负数且可表示的范围为0~255。那么对于E为负值的情况如何处理呢？

这里引入偏置 (Bias) 的概念。

IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。这里的127和1023就是Bias。也就是说，指数的值是 E= exp - Bias，即阶码减偏置

例如：2^10的E是10，所以保存成32位浮点数时，必须保存成exp=10+127=137，即10001001。此时内存中的exp中存的是10001001。

✨规则2

同样的，M存放在小数字段 f 中，我们知道，当一个小数化为二进制小数后所得到的M总是一个介于1~2之间的值，形式为1. xxxxx

因此在存数据时，考虑省略小数点前面的1（取数据的时候可以直接在前面添上），可以节省一位的存储空间，能让小数点后的数据多保存一位，提高数据的精度。

例如，M=1.01101，存到 f 中去的数据为01101，M = 1 + f

最小到-126是因为阶码只能是0000 0001，即为1，转为实际指数之后即为1 - 127 = -126

在计算机中储存的exp不是实际指数，转化为十进制的时候要先将指数转化为实际指数

实际指数=指数-127，E=exp-bias

指数：（注意这里的F只有尾数，即1.m中的m部分）

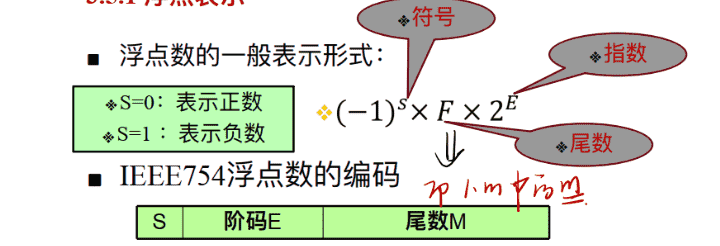
image-20221016232522878

实际指数

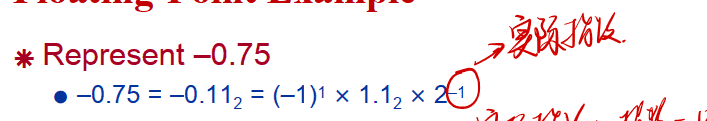
image-20221016232507539

例子：

image-20221016234837823

非规格化数

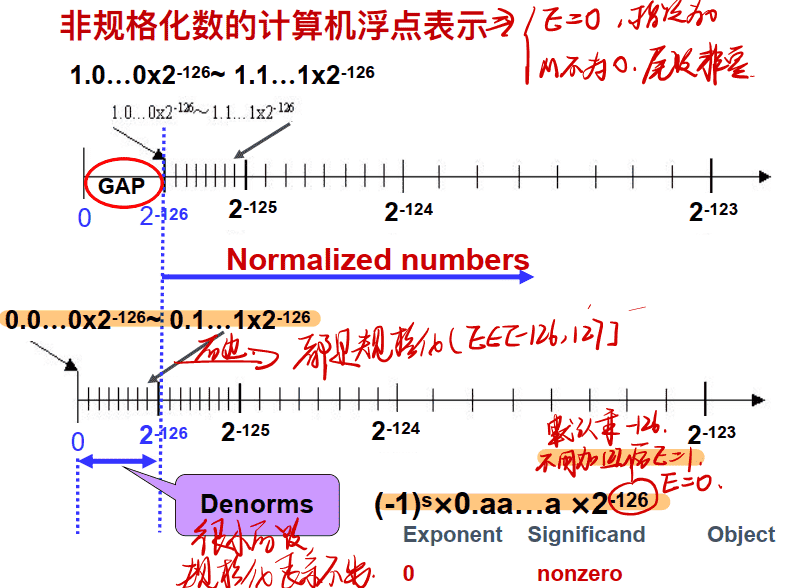
image-20221016233138178

✨规则1

当exp为全0时，此时的E = 1- Bias，也就是说1-127=-126（或者1-1023=-1022）即为真实值

补充：使指数的值为 1-Bias=-126 仍而不是简单的 -Bias 似乎是违反直觉的。在后面我们会知道，这种方式提供了一种从非规格化值平滑转换到规格化值的方法

✨规则2

有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数，即M = f ，也就是小数字段的值, 不包含隐含的开头的1

实际上，如M = 1.01101，在exp = 00000000时，存进去的是101101而不是01101

==也就是说非规范化的数默认格式是：(-1)s×0.aa…a ×2-126==

例子：

Q:给定计算机单精度浮点表示数0x80600000, 它表示的数是什么?

A： 写成⼆进制形式: 1 00000000 11000000000000000000000

​ 负数， 指数0， 尾数⾮零， 是⾮规格化数:

​ =(-1)s×0.aa…a ×2-126 ​ =(-1)1×0.11 ×2-126 ​ =-1.1 ×2-127

最⼤的正⾮规格化数为0.111111111111111111111112 × 2-126

所有正⾮规格化数在0和0.111111111111111111111112 × 2-126之间。

浮点数表示范围

image-20221016233801101

单精度浮点数最小正数（规格化）：

阶码为0000 0001，则实际指数=指数（阶码）- 127，即为-126 尾数000…000，即为1.000…000

故为1.0 × 2-126

单精度浮点数最大正数（规格化）：

阶码为1111 1110，则实际指数=指数（阶码）- 127，即为254-127=127 尾数111…111，即为1.111…111≈2.0

故为2.0 × 2127

image-20221016234737372

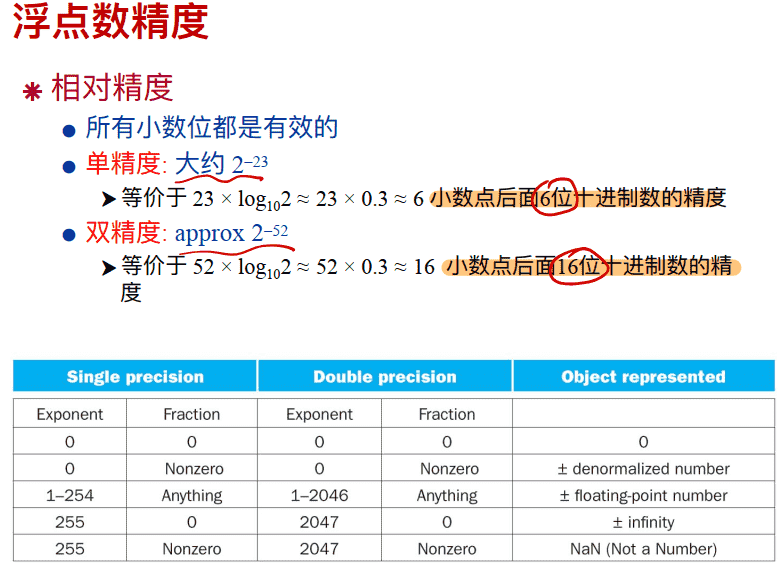
浮点数精度

image-20221016234758438

image-20221016234931828

浮点数的加减法

image-20221016235005591

十进制例子：

image-20221016235052300

二进制例子：

image-20221016235107607

浮点数乘法

image-20221016235249542

例子1： image-20221016235316688

例子2：

image-20221016235357017

浮点数除法

Division– Brief

  • Subtraction of exponents
  • Division of the significants
  • Normalisation
  • Runding
  • Sign

Accurate Arithmetic

image-20221016235847220

  • 保护位(Guard Digits): 在浮点数中间计算中， 在尾数中右边多保留两位， 第⼀位为保护位， 第⼆位为舍⼊位。
  • 舍⼊位(Round Digits)： 规格化后有效尾数⼤⼩的右边还有⼀些⾮零数字， 这个数据就需要舍⼊。⼀个舍⼊数字必须被进位到保护位的右边， 因⽽在规格化左移之后， 根据舍⼊位的数值， 可以对该结果进⾏舍⼊处理
  • 粘位（Sticky Bit） ：为进⼀步改进舍⼊处理的结果， 在舍⼊数字右边的附加位。为了更⾼的准确性， 当舍⼊数字为 B/2 时（aaaa.bbbbb100）， 需要⼀个粘位，即如果有在舍⼊数字的尾部有任何1位丢失， 则置为1。(粘位：舍入位后有数则粘位为1，否则为0)

在运算完舍入用过GRS之后，就要舍弃掉GRS，运算后的值认为GRS为000。例子如下：

image-20221021090135452

IEEE 754 round modes

IEEE标准: 四种舍⼊⽅式：

  1. 舍⼊成 正⽆穷⼤
  2. 舍⼊成 负⽆穷⼤
  3. 舍⼊成 零
  4. 舍⼊成 最接近的数:

舍⼊成 最接近的数（省缺）

  • 舍⼊数字 < B/2， 那么 截去 （B数值⼤⼩）;>B/2， 那么 舍⼊;= B/2， 那么 舍⼊成最近的偶数数字

四舍五入方法中的偶数法则

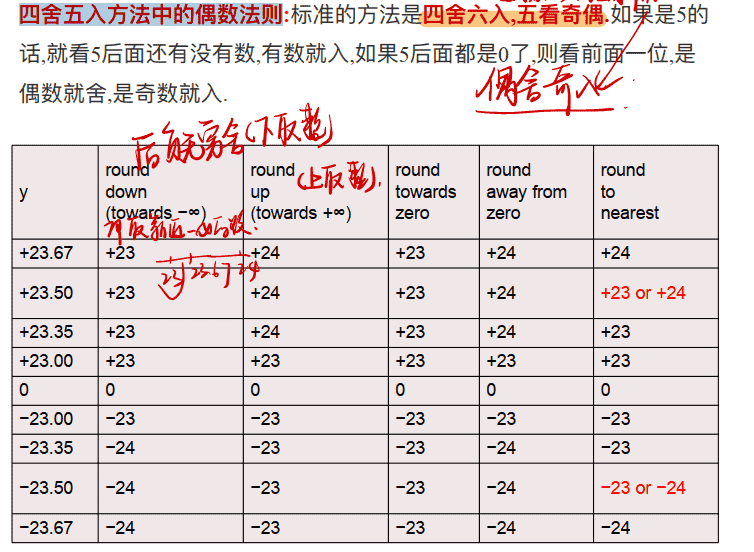
image-20221017000237592

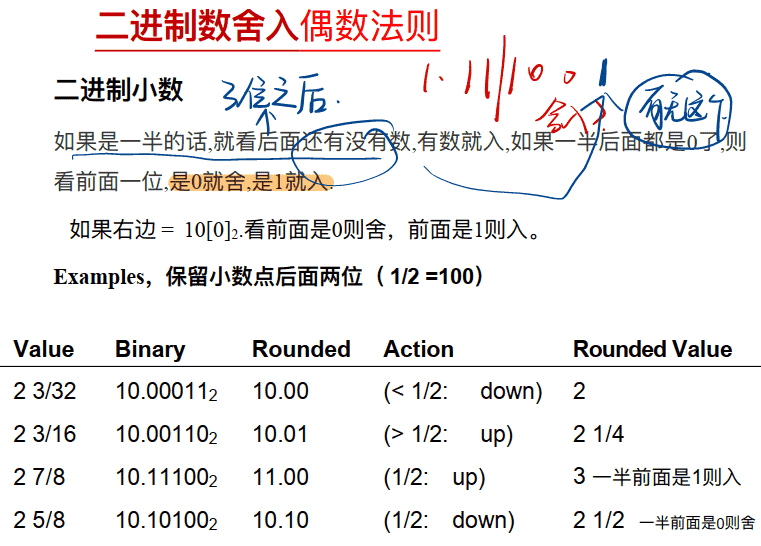
image-20221017000256782

实际保留位数之后，多保留了三位，GRS，偶数法则用于处理GRS刚好占一半时（即100），使得实际位数的最后一位为偶数（认为0属于偶数），而在二进制中，只有1和0，所以偶数法则即看最后一位：0舍1入。

只有aaaaaa.bbbbbbbb100形式的时候需要用到偶数法则，因为此时刚好是剩余数的1/2

如10.11100，0.11已经是3/4了，剩下1/4，而后面的0.00100刚好是1/8，刚好是剩余数的1/2，也就是十进制中aaa.bbb5的形式。因此要用舍入的偶数法则

只要用了一次进位后，那么得出的值的GRS对应的就是000

并行性和计算机算法： 关联性

if x + (y+ z) = (x + y) + z.

  • x = -1.5ten x 1038, y= 1.5ten X 1038, and z = 1.0

  • x + (y + z) = 0.0

  • (x+y) + z = 1.0 因为计算机表示浮点数的位数是有限的。

浮点数异常

1.0 不等于 10*0.1 (Why?) ex. 1.0 * 10.0 == 10.0 but, 0.1 * 10.0 != 1.0 ⼗进制的 0.1 == 1/16 + 1/32 + 1/256 + 1/512 + 1/4096 + … == 0.0 0011 0011 0011 0011 0011 … 对⽐⼗进制的1/3 是循环⼩数0.333333… 如果⼩数点后⾯位数有限， 那么 3 * 1/3 != 1

例子：

image-20221021090626275

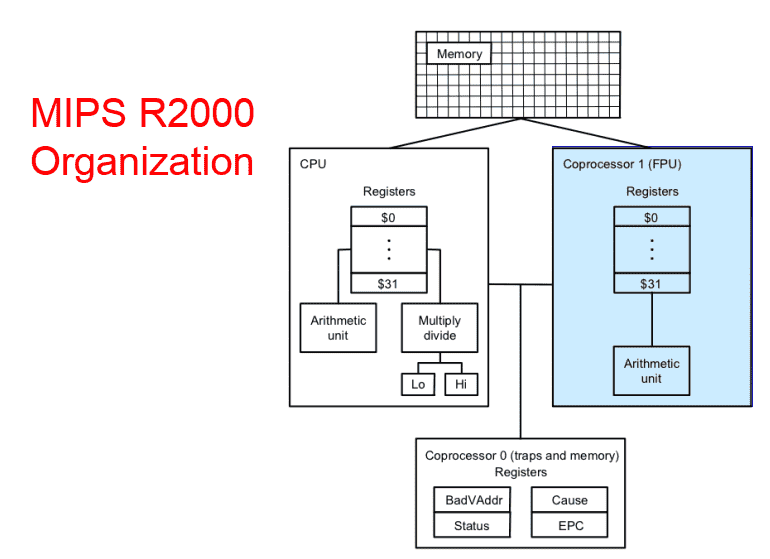
MIPS里的浮点数指令FP

  • FP 硬件是协处理器(Copprocessor)
    • 扩展 ISA 的辅助处理器
  • 独⽴的 FP 寄存器组
    • 32个 单精度: f0, f1, … f31
    • 配对组成双精度浮点数的寄存器: f0/f1, f2/f3, …
      • MIP 第 2 版 ISA ⽀持 32 × 64 位 FP reg
      • FP 指令只在浮点数寄存器组操作（即浮点数运算只用浮点寄存器）
    • 程序通常不对 FP 数据执⾏整数操作， 反之亦然
    • 更多的寄存器对减少代码⼤⼩有冲击
  • FP 内存取load 和内存写指令
  • lwc1, ldc1, swc1, sdc1
    • e.g., ldc1 f8, 32(sp)

image-20221021091600812

FP Instructions in MIPS

  • Single-precision arithmetic
    • add.s, sub.s, mul.s, div.s
      • e.g., add.s $0, f1, f6
  • Double-precision arithmetic
    • add.d, sub.d, mul.d, div.d
      • e.g., mul.d f4, f4, f6
  • Single- and double-precision comparison
    • c.xx.s, c.xx.d (xx is eq, lt, le, …)
    • Sets or clears FP condition-code bit
      • e.g. c.lt.s f3, f4
  • Branch on FP condition code true or false
    • bc1t, bc1f
      • e.g., bc1t TargetLabel

即加上.s变成单精度指令，加上.d变成双精度

总结

  • 数字本身并没有内在含义: 操作确定它们是 ASCII字符， 还是整数、 浮点数。
  • 除法和乘法可以使⽤相同的硬件: 在MIPS处理器中的Hi（余数和乘积的高位） & Lo（商和乘积低位） 寄存器
  • 浮点数的处理基本上沿⽤科学计数法的⼿算⽅法， 对尾数的⼤⼩的处理使⽤乘法和除法的整数算法
CATALOG
    FEATURED TAGS
    Computer-Organization NOTES Project AI OS ML PatternRecognition Blog Distributed-System ANN CPU设计 CompilationPrinciple