3-2-2 DIvision
n-bit 操作数产⽣ n-bit 商 quotient 和余数 remainder
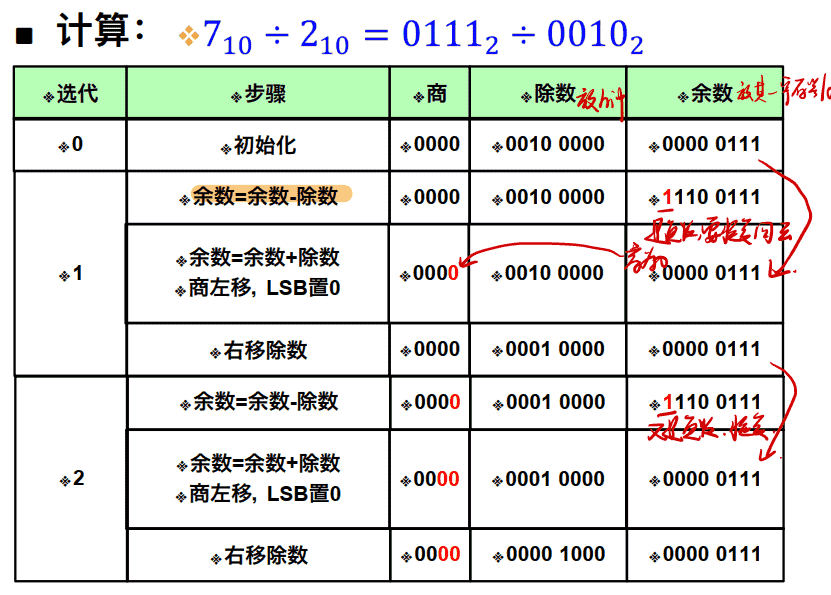
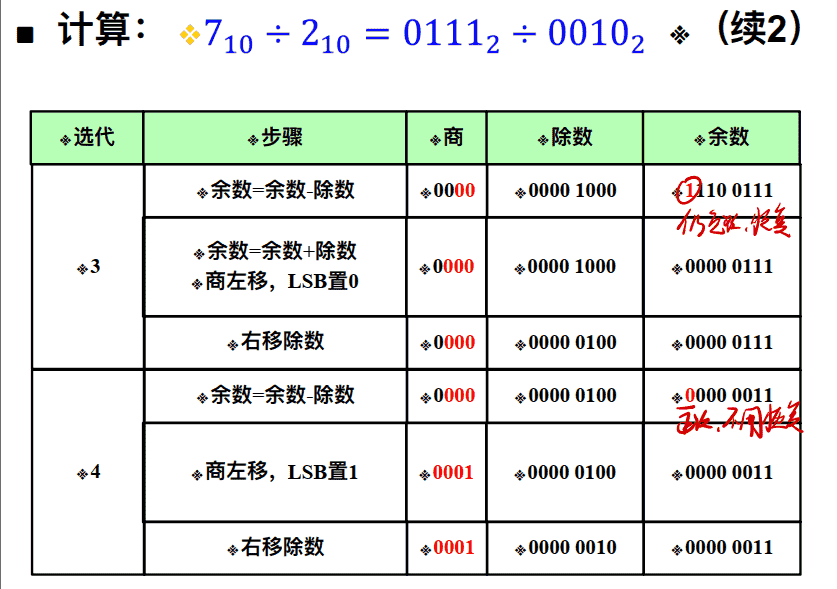
第⼀种除法算法
32位⼆进制除法硬件电路 :
- 32位被除数放在64位余数寄存器的低32位中;
- 32位除数放在64位除数寄存器的高32位, 低32位填0
- 32位商初始化为0
- 移位操作:商左移,除数右移

例子:
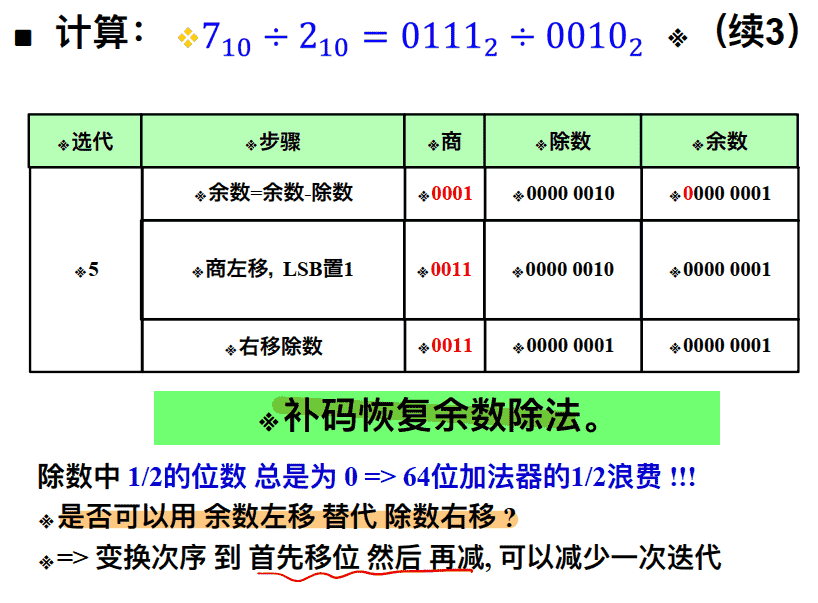
启发:
- 变换次序 到 ⾸先移位 然后 再减, 可以减少⼀次迭代
- ⽤ 余数左移 替代 除数右移 (商也是左移)
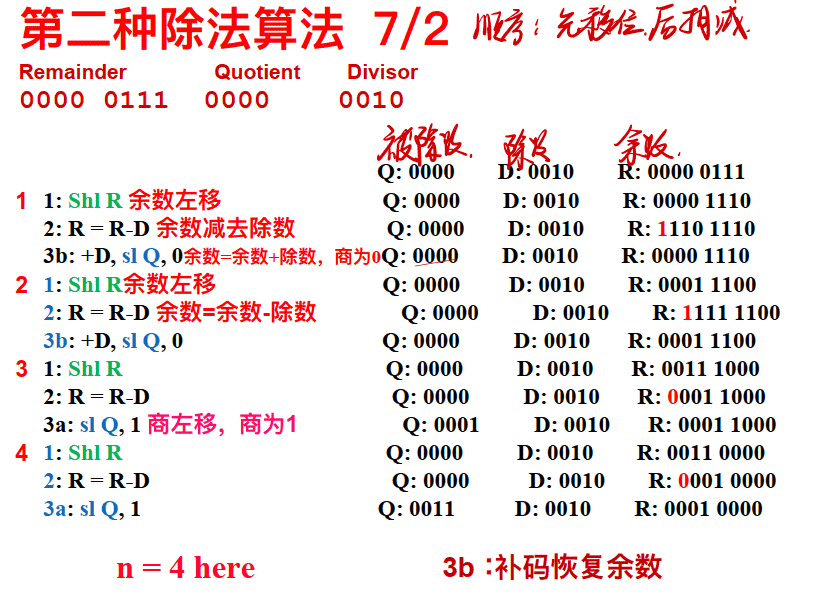
第二种除法算法
- 将除数寄存器向右移位改为余数寄存器向左移位,除数寄存器保持不变
- 除数寄存器为32位, ALU为32位
- 移位操作:余数左移,商左移
例子:
Quotient是商
第⼆种除法的启示 :(即第三种除法算法的内容)
- 通过在左移中,与余数合并, 取消商寄存器象前⾯⼀样, 以左移余数开始.
- 其后, 由于余数寄存器的移动即可移动左半部的余数,⼜可移动右半部的商,因⽽每次循环只包括两步.
- 将两个寄存器联合在⼀起 和 循环内新的操作次序的导致余数多左移⼀次
- 因⽽, 最后⼀步 必须将这个寄存器左半部中的余数移回
第三种除法算法
tips:这种算法一开始会先左移一次余数寄存器,所以最后一步的时候左半部分的寄存器中余数要右移一次移回(右半部分不用移)
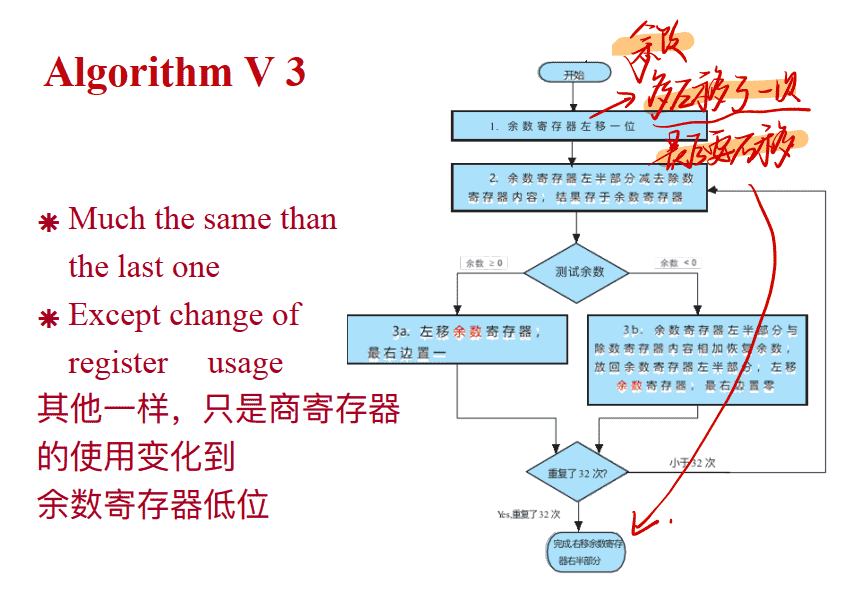
==算法流程==
- 第0步时,余数寄存器高32位初始化为0,低32位存入被除数,然后余数寄存器整体64位左移一位,最后补0
- 之后的32步,执行:
- 余数=余数-除数:余数寄存器的余数(高32位or左半边)减去除数,结果存到高32位
- 若余数大于0(第一位为0),左移余数寄存器(64位都移动),最右边置1(低32位存商)
- 若余数小于0(第一位为1),余数恢复为没有减除数时状态,左移余数寄存器(64位都移动),最右边置0(低32位存商)
- 最后第33步的时候,右移余数部分(即左半部分or高32位,右半部分不用右移),然后得到答案:高32位为余数,低32位为商
tips:最后一步容易被忽略
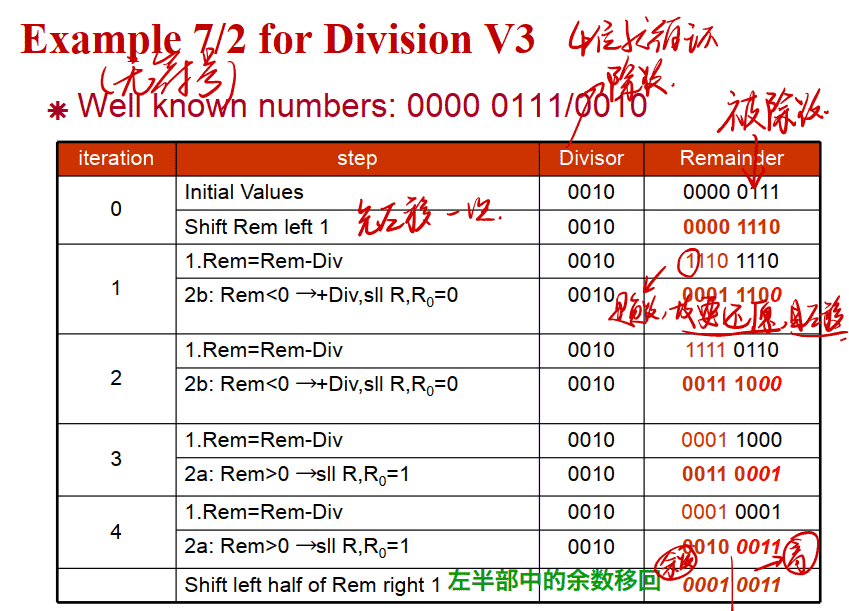
例子:
有符号除法
被除数和余数的符号必须相同
被除数=除数×商+余数
有符号除法: 最简单的⽅法是记住符号, 进⾏正数除法, 并根据需要对商和余数进⾏修正
- 注: 被除数和余数的符号必须相同
- 注: 如果除数和被除数的符号不同, 商为负
商有可能很⼤: 如果⼀个64位整数除以 1, 那么商就为 64 位 (称为“饱和”: saturation)
如果余数不与被除数符号一致, 会产生被除数和除数的符号不同, 商的绝对值得到不同的结果。

Fast Division
