3-1 ALU Design
ALU:Arithmetic & Logic Unit
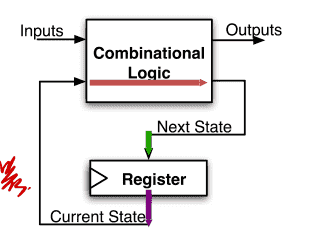
同步数字系统由两部分电路组成 :
- 组合逻辑电路(CL)
- 输出只是输⼊的函数
- E.g., 加法电路 add A, B (ALUs)
- 时序逻辑电路(SL)
- 电路有 “记忆” ,能存储信息
- “State Elements”状态元
- 有记忆能⼒的寄存器(Registers)
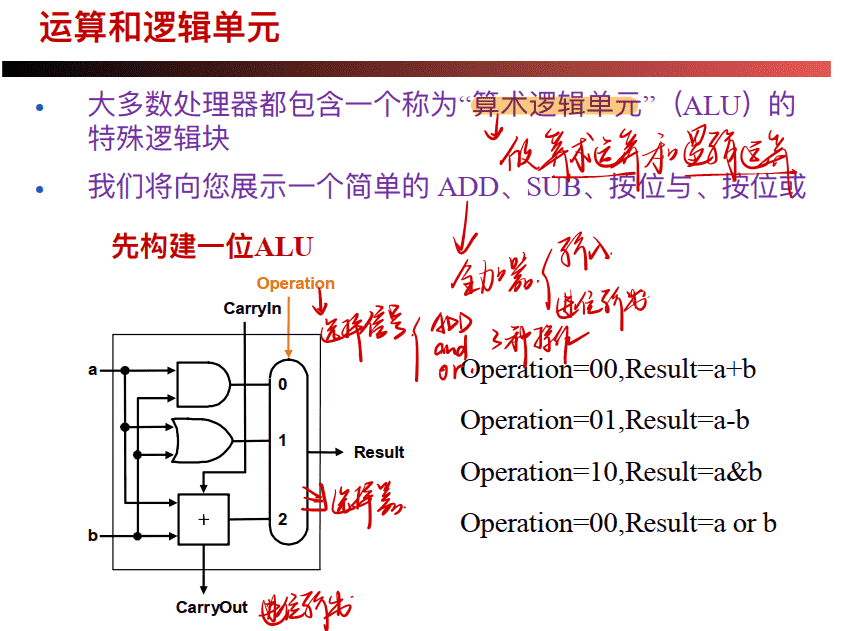
运算和逻辑单元
MUX 数据选择器
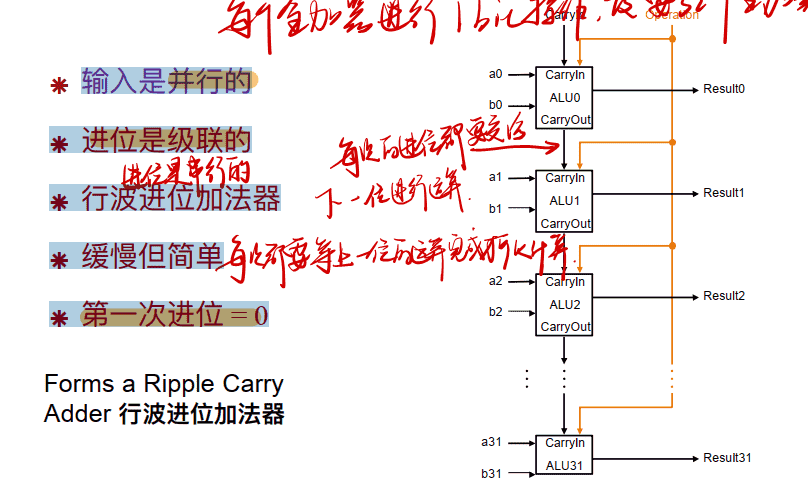
行波进位加法器
- 输⼊是并行的
- 进位是级联的
- 行波进位加法器
- 缓慢但简单
- 第⼀次进位 = 0
减法的设计
- ⼆进制补码⽅法: 只需将 b 取反并相加, Binvert =1, a+b反。
- ⼀个优雅的解决⽅案 - 在位 0 上使⽤进位 Carrylin(减法,Binvert =1, 加法, Binvert =0)
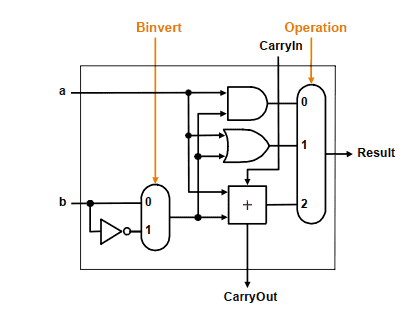
行波进位加法器的时间
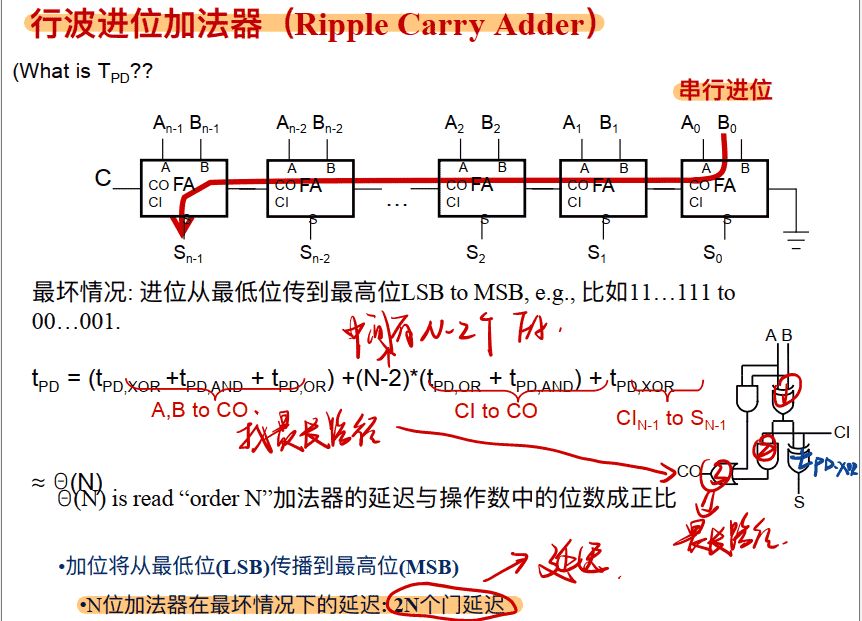
公式的优化
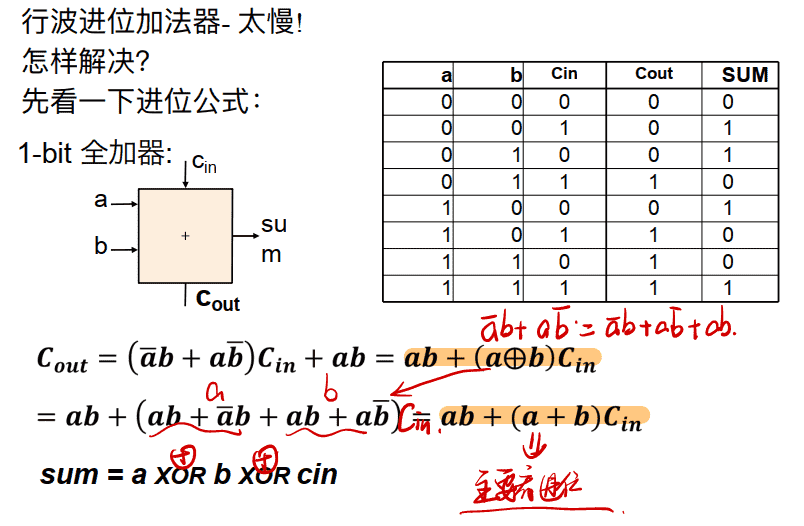
- 因为此时ab是冗余项,a+b和a⊕b就差一个a=b=1的情况,而这种情况以及被前面一个ab包含了,所以在后面一个多项式中有没有加一个ab都不影响结果
先行进位加法器(并行进位加法器 )
进位 ci+1=aibi + (ai + bi)ci
定义G 为产生进位 ** **Gi=aibi (aibi同时为1的话,则会有进位), 定义Pi=ai + bi为传播进位(ai和bi其中一个为1,ci也为1时,也会产生进位)
因此 ==ci+1=Gi +Pici==
==Si=ci⊕Pi==

变成了 only 3 levels of logic,表示成了三级 3-level逻辑
并行进位的特点
- 同时产⽣进位(通过计算 Pi 和 Gi)
- 加法延时缩短 (变成3-evel)
- 实现相对复杂 (需要多个门来计算Pi 和 Gi)
局部(级联)先行进位加法器
- 实现全先⾏进位加法器的成本太⾼(想象Cin31的逻辑⽅程的⻓度)
- ⼀般性经验:
- 连接⼀些N位先⾏进位加法器, 形成⼀个⼤加法器
- 例如: 连接4个8位进位先⾏加法器, 形成1个32位局部先⾏进位加法器
即:==分组并行进位加法器(组内并行, 组间传递(串行))==
⽤ CLA 原理构建⼀个⼤加法器
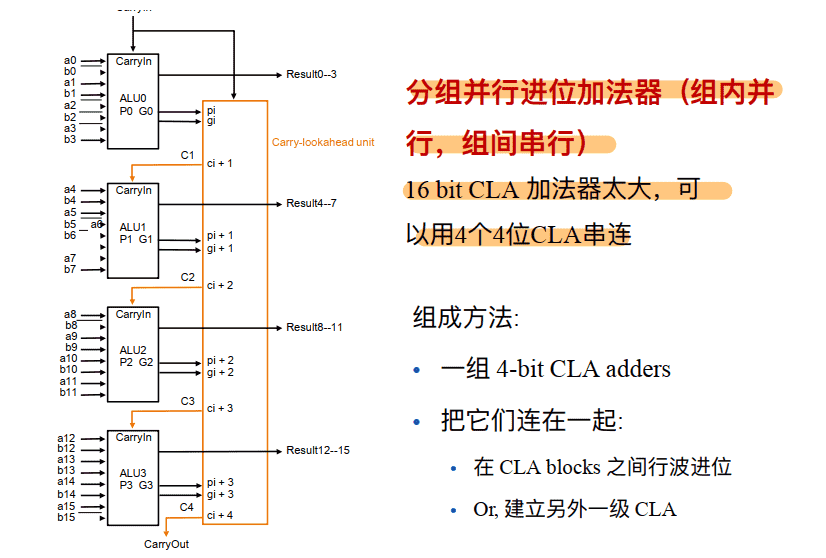
加法器/减法器为⼀体: 减法“求反加⼀” (即求补码)
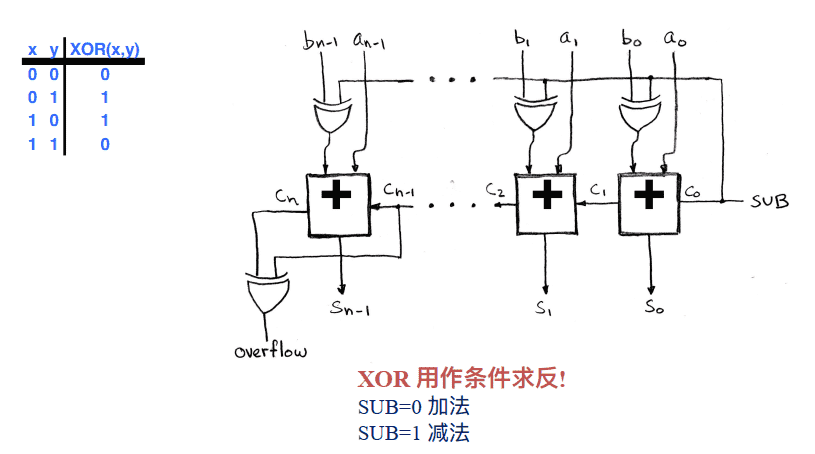
条件码

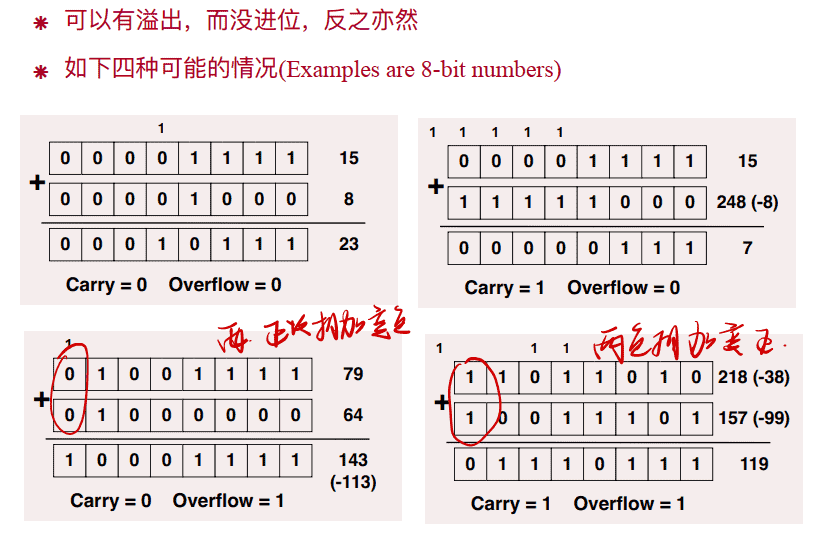
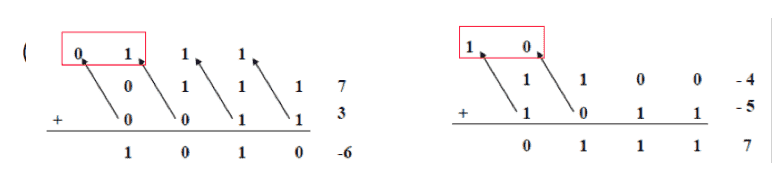
进位与溢出举例
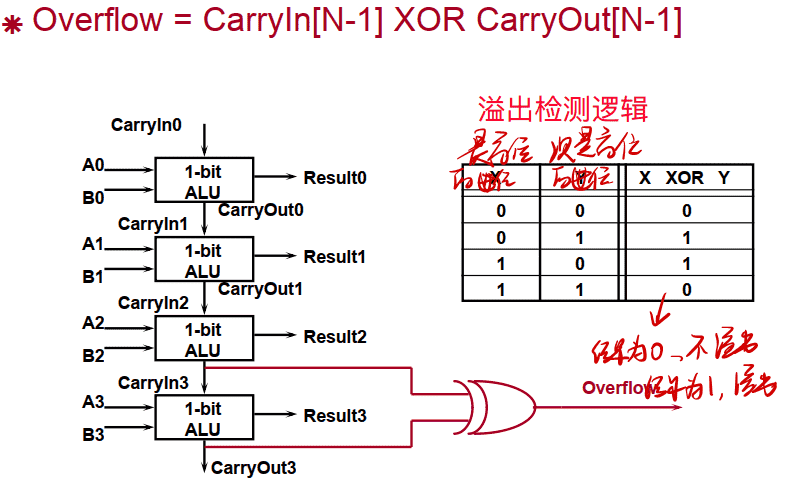
溢出检测 Overflow Detection Logic (还有笔记可以参考2-1中的溢出检测)
Overflow = CarryIn[N-1] XOR CarryOut[N-1] 即 最高位进位 异或 次高位进位
为0则不溢出,为1则溢出
- 溢出: 结果超出了正常的表示范围(太⼤ 和 太⼩) 例如: - 8 < = 4位⼆进制数 <= 7 (-2n 到 2n-1)
- 当对具有不同符号的操作数进⾏加法运算时, 不会出现溢出!
- 当进⾏同号加法时, 出现溢出: •两个正数相加, 结果为负 •两个负数相加, 结果为正
- 溢出可以⽤如下⽅法检测: •输⼊到最⼤位的进位 != 从最⼤位输出的进位()
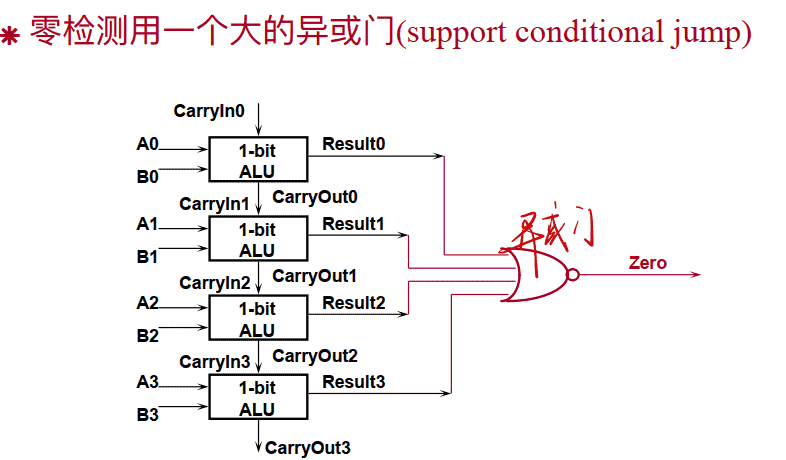
零检测 Zero Detection Logic
零检测用⼀个大的异或门(support conditional jump)
Set on Less Than (小于判断)
- Slt rd,rs,rt
- If rs < rt, rd=1, else rd=0 N⊕V(N为运算结果小于0标志,V为运算结果溢出标志)
- 除了最低位, 所有位为零
- rs - rt, 如果结果是负的, 则 rs < rt
- 使用符号位作为判断
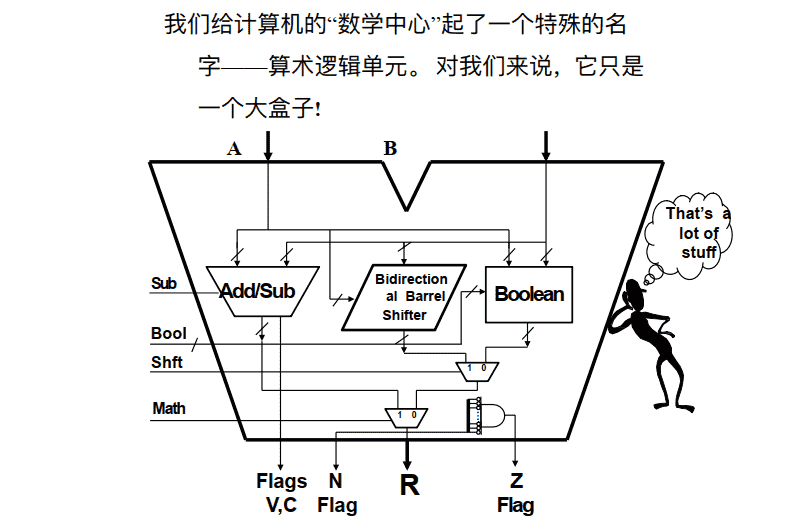
ALU组合到⼀起
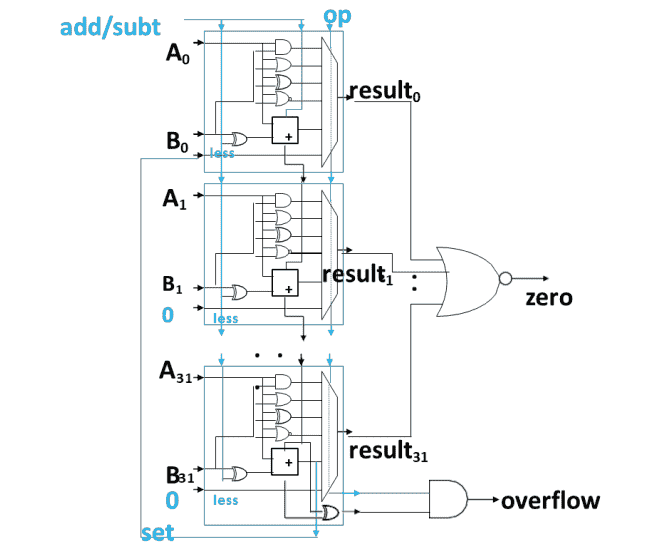
Shifter Design 移位
移位可以⽤于乘法或除法运算:
- 左移N bits 相当于数字乘以 2的N次方 Ex: 00001 « 2 = 00100 (1 × 22 = 4) Ex: 11101 « 2 = 10100 (-3 × 22 = -12)
- 算数右移 N 位 相当于数字除以 2的N次方 Ex: 01000 »> 2 = 00010 (8 ÷ 22 = 2) Ex: 10000 »> 2 = 11100 (-16 ÷ 22 = -4)
移位之后进行0扩展,即在空出的地方补0
-
X « n 等价于 2n*X
-
X » n 等价于 $X \over 2^n$
三种移位器
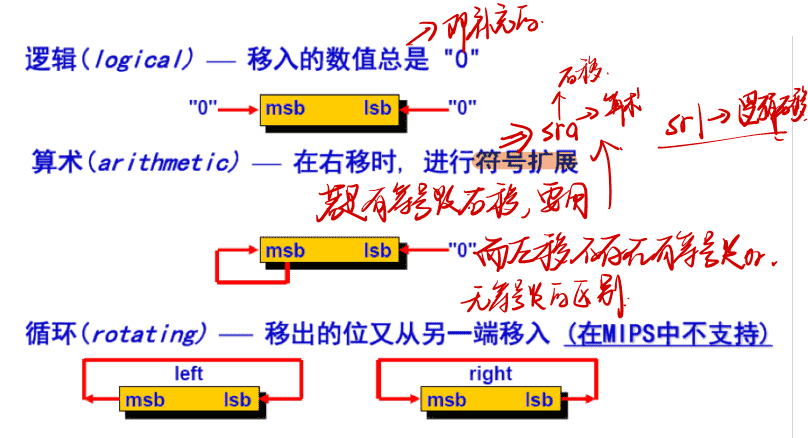
移位实现 Let’s simplify
- 移动一位

- 左移2位
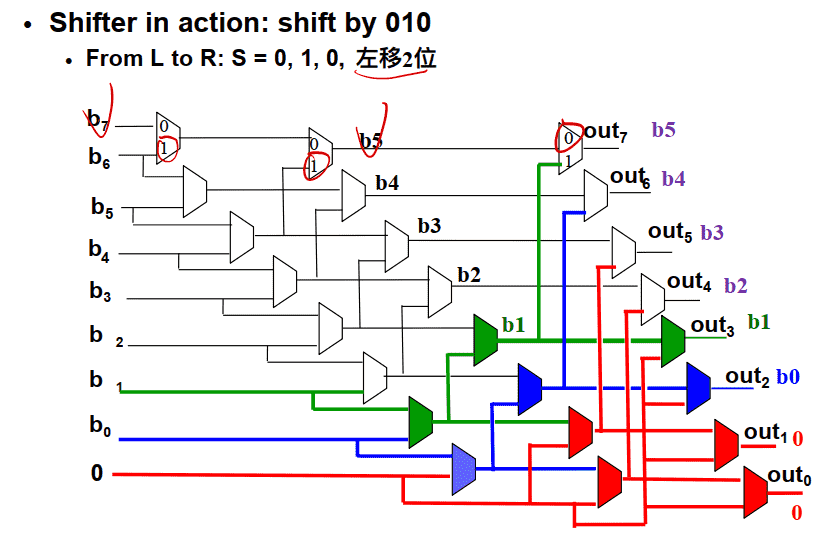
- 移3位
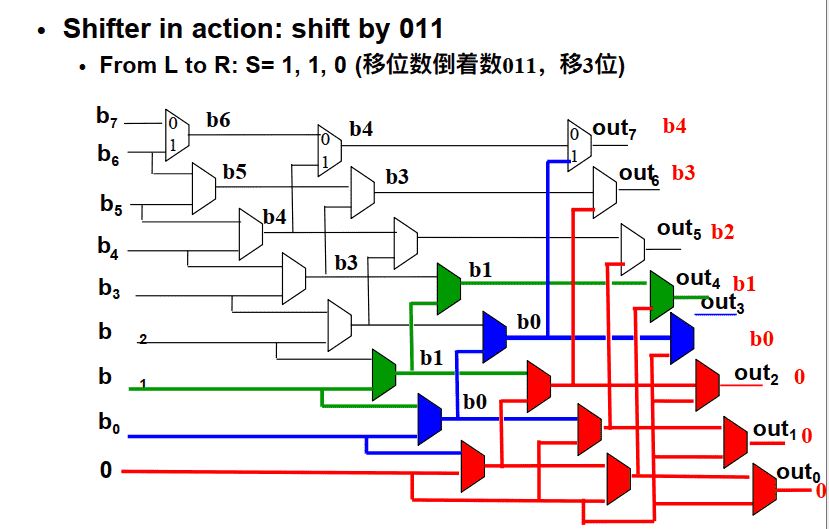
- 移7位
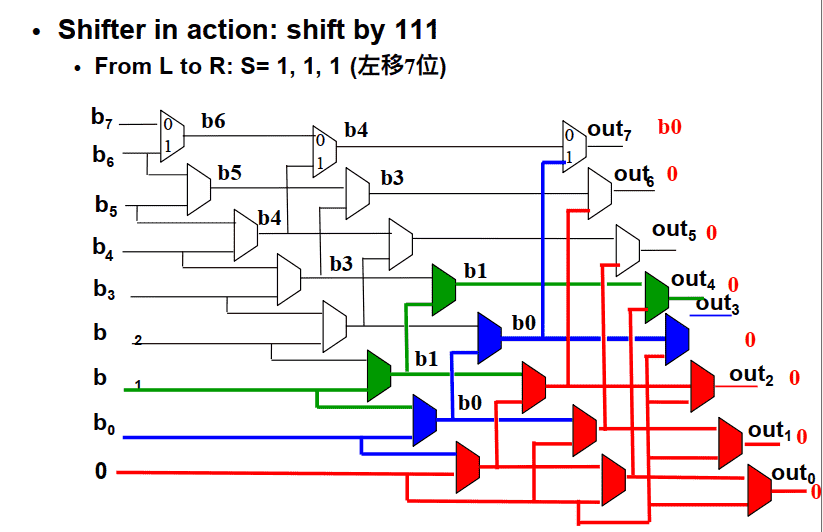
布尔运算
对位组执⾏逻辑运算也很有⽤?
- ANDing is useful for “masking” off groups of bits. ex. 10101110 & 00001111 = 00001110 (mask selects last 4 bits)
- ANDing is also useful for “clearing” groups of bits. ex. 10101110 & 00001111 = 00001110 (0’s clear first 4 bits)
- ORing is useful for “setting” groups of bits. ex. 10101110 | 00001111 = 10101111 (1’s set last 4 bits)
- XORing is useful for “complementing” groups of bits. ex. 10101110 ^ 00001111 = 10100001 (1’s invert last 4 bits)
- NORing is useful for.. uhm… ex. 10101110 # 00001111 = 01010000 (0’s invert, 1’s clear)
An ALU, at Last