The Instruction Set Architecture
计算机中数的表示基本问题(数的二进制表示)
ASCII码有八位,其中第一位用于奇偶校验,其余七位用于编码字符
1.正整数的编码
-
Memorize the first 10 powers of 2 25=32 210=1024
-
Memorize the prefixes for powers of 2 that are multiples of 10(记住2的10的倍数幂)
210 = Kilo (1024) 220 = Mega (1024×1024) 230 = Giga (1024×1024×1024) 240 = Tera (1024×1024×1024×1024) 250 = Peta (1024×1024×1024 ×1024×1024) 260 = Exa (1024×1024×1024×1024×1024×1024)
二进制转十进制的小技巧

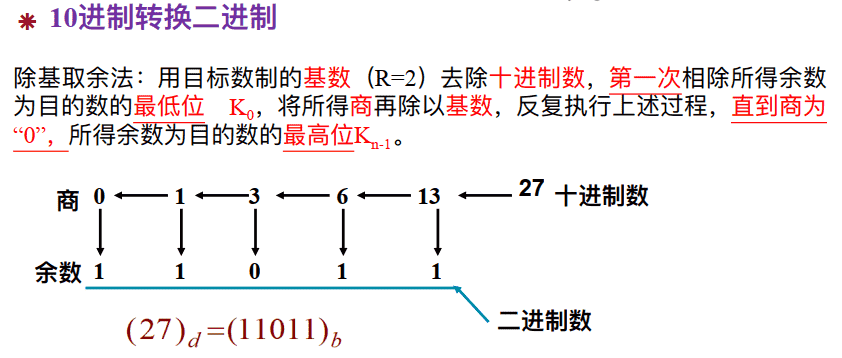
十进制转二进制
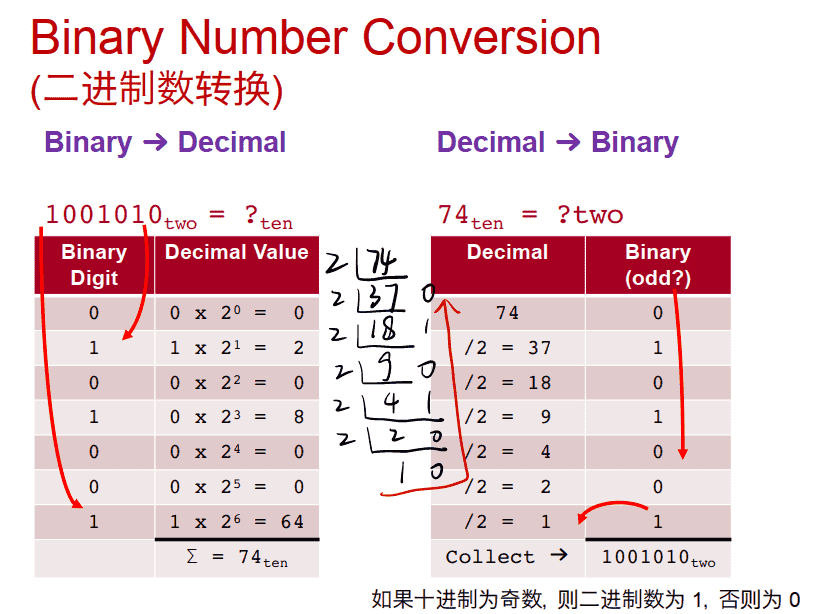
若是二进制转十六进制,可从右往左每四个一组,转为十六进制
| 进制基数(radix) | 前缀 | 示例 |
|---|---|---|
| 二进制 binary | 0b 0B | 0b11 = 2+1=3 |
| 八进制 octal | 0o 0O 0 | 0o11 = 8+1=9 |
| 十进制 decimal | 无前缀 | 11 = 11 |
| 十六进制 hex | 0x 0X | 0x11 |
2.有符号数的编码
最高位(最左边)为符号位,0为正,1为负
- 正数的反码的补码都为本身
- 负数的反码为除了符号位其他都按位取反,补码为反码加一

减法即为加这个负数的补码

在扩展时,要进行符号扩展,如:

3.非整数的编码
3-1 定点表示

两种方法将二进制转为十进制

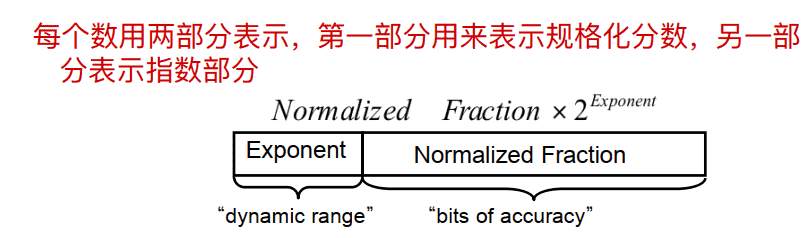
3-2 浮点表示
此表示法使⽤两个字段来表示每个数字. 第⼀部分表示归⼀化分数( normalized fraction) (称为尾数( significand ) ), 第⼆部分表示指数部分 (i.e. 浮点表示的⼆进制数的⼩数点位置)
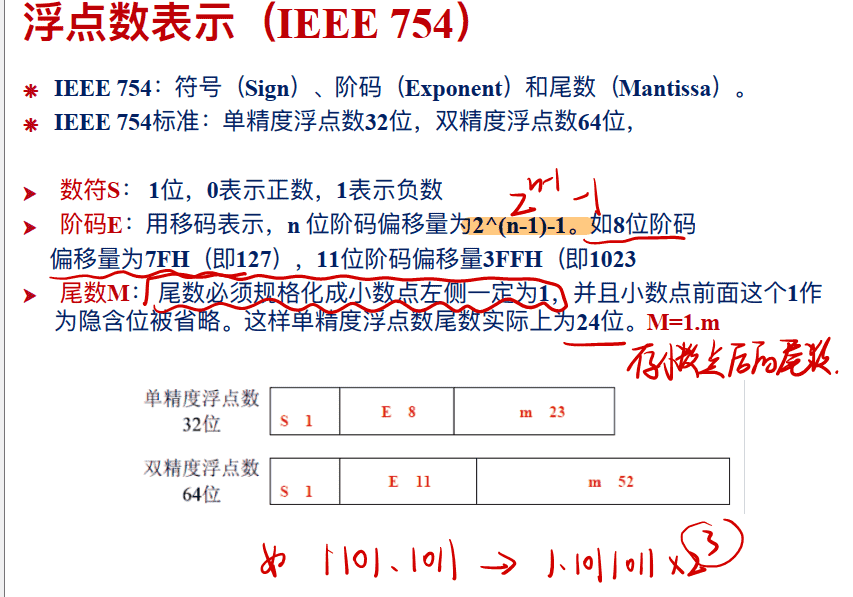
范围阶码范围:-126-127,即(ob0000 0001-127=1-127=-126到ob1111 1110 - 127=(2^8-1)-1 - 127=254-127=127)

转为IEEE754步骤
- 第一位为符号位
- 中间为阶码,是用127+n,n为2n中的n(指数),即移动小数点位数,然后转为二进制数
- 最后为尾数,是移动小数点后1.m中的m
浮点数的表示约定 单精度浮点数和双精度浮点数都是⽤IEEE 754标准定义的, 其中有⼀些特殊约定, 例如:
- 当阶码Exp=0, 尾数M=0时, 表示0。
- 当阶码Exp=255(1111 1111), 尾数M=0时, 表示⽆穷⼤, ⽤符号位来确定是正⽆穷⼤还是负⽆穷⼤。
- 当阶码Exp=255(1111 1111), M≠0时, 表示NaN(Not a Number, 不是⼀个数)
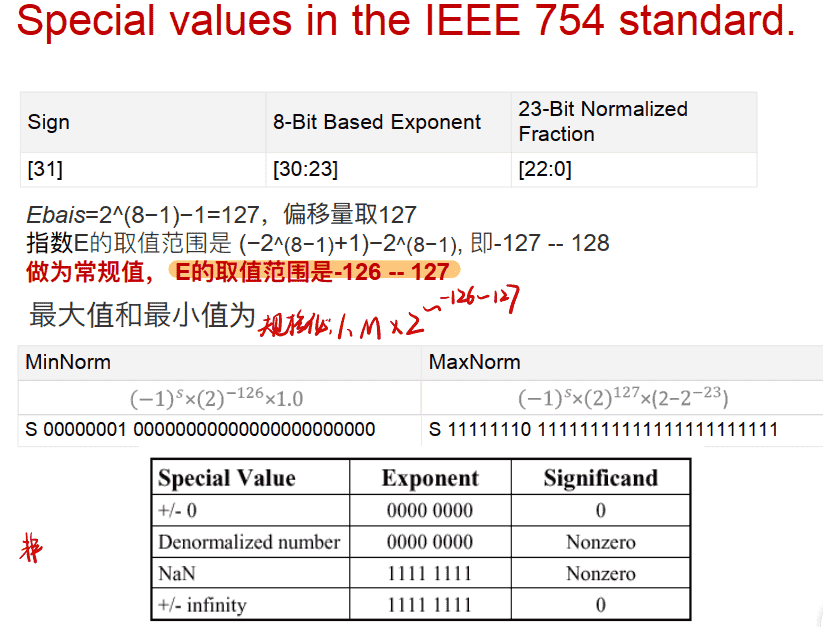
即指数E=阶码Exponent-127,阶码为无符号数,最小为0000 0001(规范化时),此时1-127=-126,最大为1111 1110,即2^8-1-1=254,254-127=127
非规范数一定是指数为0,尾数不为零,规范数指数一定不为0,尾数可以为0,因为最大最小数为
- 规范数最小正值 0 0000 0001 000000….000
- 规范数最大值 0 1111 1110 111111….111 (指数最大为127,因此指数部分不是1111 1111)
- 非规范数最小正值 0 0000 0000 000000….001 (尾数一定不为0),若尾数为0则不表示非规范化数而是表示0
- 非规范最大值 0 0000 0000 111111….111

非规范浮点数中默认指数E的取值为-126,即一定是2-126,而且尾数也不是化为1.m,而是0.m,然后再转为十进制
4.溢出overflow
当两个符号相同的数相加或两个符号相异的数相减才可能产生溢出。
根据数据位进位情况判断溢出
| 符号位的进位Cs(即最高位最后有无进位) | 最高数值位的进位C1(即次高位最后有无进位) | |
|---|---|---|
| 上溢 | 0 | 1 |
| 下溢 | 1 | 0 |
即逻辑判断表达式V = Cs ⊕ C1。若V=0,表示无溢出;V=1,表示有溢出
【例】设机器字长为8位(含一位符号位),A=15,B=-24,C=124,求[A+C]补和[B-C]补。
【分析】:[A+C]补=00001111+01111100=10001011(真值-117) [B-C]补=[B]补+[-C]补=11101000+10000100=01101100 (真值+108)
上例[A+C]补的计算结果可知,Cs = 0 ,C1=1,发生了上溢;[B-C]补,Cs =1,C1=0,发生了下溢。
即Cs 与C1不同时发生溢出,逻辑判断表达式V = Cs ⊕ C1。若V=0,表示无溢出;V=1,表示有溢出
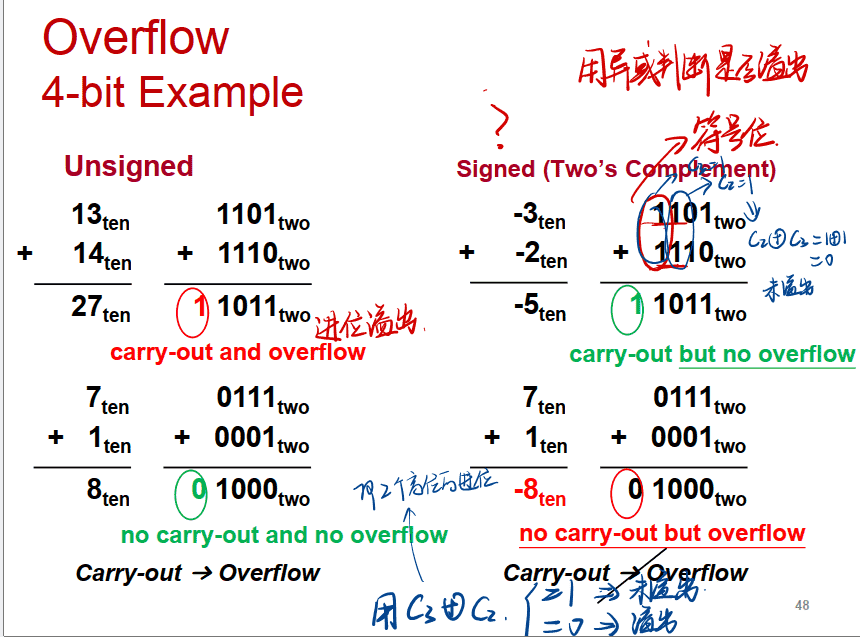
(蓝色字迹笔记写错了,0是未溢出,1是溢出)